A set of things that are in order is called a Sequence and when Sequences start to follow a certain pattern, they are known as Progressions. Progressions are of different types like Arithmetic Progression, Geometric Progressions, Harmonic Progressions.
The sum of a particular Sequence is called a Series. A Series can be Infinite or Finite depending upon the Sequence, If a Sequence is Infinite, it will give Infinite Series whereas, if a Sequence is finite, it will give Finite series.
Let’s take a finite Sequence:
a1, a2, a3, a4, a5,……….an
The Series of this Sequence is given as:
a1+ a2+ a3+ a4+a5+……….an
The Series is also denoted as :
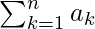
Series is represented using Sigma (∑) Notation in order to Indicate Summation.
Geometric Series
In a Geometric Series, every next term is the multiplication of its Previous term by a certain constant and depending upon the value of the constant, the Series may be Increasing or decreasing.
Geometric Sequence is given as:
a, ar, ar2, ar3, ar4,….. {Infinite Sequence}
a, ar, ar2, ar3, ar4, ……. arn {Finite Sequence}
Geometric Series for the above is written as:
a + ar + ar2 + ar3 + ar4 +…. {Infinite Series}
a + ar + ar2 + ar3 + ar4 +….. arn {Finite Series}
Where. a = First term
r = Common Factor
Can the values of ‘a’ and ‘r’ be 0?
Answer: No, the value of a≠0, if the first term becomes zero, the series will not continue. Similarly, r≠0.
Geometric Series Formula
The Geometric Series formula for the Finite series is given as,
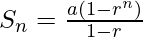
where, Sn = sum up to nth term
a = First term
r = common factor
Derivation for Geometric Series Formula
Suppose a Geometric Series for n terms:
Sn = a + ar + ar2 + ar3 + …. + arn-1 ⇢ (1)
Multiplying both sides by the common factor (r):
r Sn = ar + ar2 + ar3 + ar4 + … + arn ⇢ (2)
Subtracting Equation (1) from Equation (2):
(r Sn – Sn) = (ar + ar2 + ar3 + ar4 + … arn) – (a + ar + ar2 + ar3 +… + arn-1)
Sn (r-1) = arn – a
Sn (1 – r) = a (1-rn)
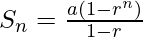
Note: When the value of k starts from ‘m’, the formula will change.
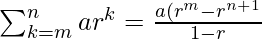 , when r≠0
, when r≠0
For Infinite Geometric Series
n will tend to Infinity, n⇢∞, Putting this in the generalized formula:
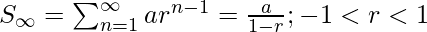
Nth term for the G.P. : an = arn-1
Product of the Geometric series
The Product of all the numbers present in the geometric progression gives us the overall product. It is very useful while calculating the Geometric mean of the entire series.
Geometric Mean
By definition, it is the nth root of Product of n numbers where ‘n’ denotes the number of terms present in the series. Geometric Mean differs from the Arithmetic Mean as the latter is obtained by adding all terms and dividing by ‘n’, while the former is obtained by doing the product and then taking the mean of all the terms.
Significance of Geometric Mean
Geometric mean is calculated because it informs the compounding that is occurring from period to period. It tells the central behavior of the Progression by taking the mean of Geometric progression. For example, The growth of bacteria can easily be analyzed using Geometric mean. In short, Longer the Time Horizon or the values in the series differs from each other, the compounding becomes more critical, and hence, Geometric mean is more appropriate to use.
Formula for Geometric Mean
![Rendered by QuickLaTeX.com \bar{X}_{geom}=\sqrt [n]{x_{1}.x_{2}.x_{3}...x_{n}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cf8466bc6864808dca6aed0440561907_l3.png)
where,

Question 1: What is the Geometric mean 2, 4, 8?
Answer:
According to the formula,
![Rendered by QuickLaTeX.com =\sqrt [3]{(2)(4)(8)}\\=4](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0e1d6eb0d2a837f51768e14a6148a28d_l3.png)
Question 2: Find the first term and common factor in the following Geometric Progression:
4, 8, 16, 32, 64,….
Answer:
Here, It is clear that the first term is 4, a=4
We obtain common Ratio by dividing 1st term from 2nd:
r = 8/4 = 2
Question 3: Find the 8th and the nth term for the G.P: 3, 9, 27, 81,….
Answer:
Put n=8 for 8th term in the formula: arn-1
For the G.P : 3, 9, 27, 81….
First term (a) = 3
Common Ratio (r) = 9/3 = 3
8th term = 3(3)8-1 = 3(3)7 = 6561
Nth = 3(3)n-1 = 3(3)n(3)-1
= 3n
Question 4: For the G.P. : 2, 8, 32,…. which term will give the value 131073?
Answer:
Assume that the value 131073 is the Nth term,
a = 2, r = 8/2 = 4
Nth term (an) = 2(4)n-1 = 131073
4n-1 = 131073/2 = 65536
4n-1 = 65536 = 48
Equating the Powers since the base is same:
n-1 = 8
n = 9
Question 5: Find the sum up to 5th and Nth term of the series: 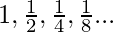
Answer:
a= 1, r = 1/2
Sum of N terms for the G.P, 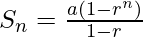
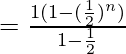
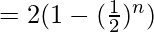
Sum of first 5 terms ⇒ a5 = 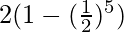
= 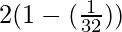
= 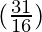
Question 6: Find the Sum of the Infinite G.P: 0.5, 1, 2, 4, 8, …
Answer:
Formula for the Sum of Infinite G.P: 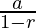 ; r≠0
; r≠0
a = 0.5, r = 2
S∞= (0.5)/(1-2) = 0.5/(-1)= -0.5
Question 7: Find the sum of the Series: 5, 55, 555, 5555,… n terms
Answer:
The given Series is not in G.P but it can easily be converted into a G.P with some simple modifications.
Taking 5 common from the series: 5 (1, 11, 111, 1111,… n terms)
Dividing and Multiplying with 9: 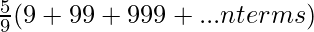
⇒ ![Rendered by QuickLaTeX.com \frac{5}{9}[((10+(10)^2+(10)^3+...n terms)-(1+1+1+...n terms)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-30229bc71f9129e244d621b16fbb1b44_l3.png)
⇒![Rendered by QuickLaTeX.com \frac{5}{9}[(\frac{10((10)^n-1)}{10-1})-(n)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0eac555f963ca6957d4261b29a5e77d9_l3.png)
⇒ ![Rendered by QuickLaTeX.com \frac{5}{9}[(\frac{10((10)^n-1)}{9})-(n)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3522c312747eef80d0ad6f0ef4bb69a9_l3.png)
Share your thoughts in the comments
Please Login to comment...