Find subfactorial of a number
Last Updated :
08 Oct, 2021
Given an integer N, the task is to find the subfactorial of the number represented as !N. The subfactorial of a number is defined using below recurrence relation of a number N:
!N = (N-1) [ !(N-2) + !(N-1) ]
where !1 = 0 and !0 = 1
Some of the subfactorials are:
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|
| !n | 1 | 0 | 1 | 2 | 9 | 44 | 265 | 1, 854 | 14, 833 | 133, 496 | 1, 334, 961 | 14, 684, 570 | 176, 214, 841 | 2, 290, 792, 932 |
|---|
Examples:
Input: N = 4
Output: 9
Explanation:
!4 = !(4-1)*4 + (-1)4 = !3*4 + 1
!3 = !(3 – 1)*3 + (-1)3 = !2*3 – 1
!2 = !(2 – 1)*2 + (-1)2 = !1*2 + 1
!1 = !(1 – 1)*1 + (-1)1 = !0*1 – 1
Since !0 = 1, therefore !1 = 0, !2 = 1, !3 = 2 and !4 = 9.
Input: N = 0
Output: 1
Approach: The subfactorial of the number N can also be calculated as:

Expanding this gives
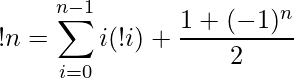
=> !N = ( N! )*( 1 – 1/(1!) + (1/2!) – (1/3!) …….. (1/N!)*(-1)N )
Therefore the above series can be used to find the subfactorial of number N. Follow the steps below to see how:
- Initialize variables, say res = 0, fact = 1 and count = 0.
- Iterate over the range from 1 to N using i and do the following:
- Update fact as fact*i.
- If the count is even then update res as res = res – (1 / fact).
- If the count is odd then update res as res = res + (1 / fact).
- Increase the value of count by 1.
- Finally, return fact*(1 + res).
Below is the implementation of the above approach:
C++
#include <iostream>
using namespace std;
double subfactorial(int N)
{
double res = 0, fact = 1;
int count = 0;
for (int i = 1; i <= N; i++) {
fact = fact * i;
if (count % 2 == 0)
res = res - (1 / fact);
else
res = res + (1 / fact);
count++;
}
return fact * (1 + res);
}
int main()
{
int N = 4;
cout << subfactorial(N);
return 0;
}
|
Java
import java.util.*;
class GFG {
static double subfactorial(int N)
{
double res = 0, fact = 1;
int count = 0;
for (int i = 1; i <= N; i++) {
fact = fact * i;
if (count % 2 == 0)
res = res - (1 / fact);
else
res = res + (1 / fact);
count++;
}
return fact * (1 + res);
}
public static void main(String[] args)
{
int N = 4;
System.out.println((int)(subfactorial(N)));
}
}
|
Python3
def subfactorial(N):
res = 0
fact = 1
count = 0
for i in range(1, N+1):
fact = fact * i
if (count % 2 == 0):
res = res - (1 / fact)
else:
res = res + (1 / fact)
count += 1
return fact * (1 + res)
if __name__ == "__main__":
N = 4
print(subfactorial(N))
|
C#
/// C# program for the above approach
using System;
using System.Collections.Generic;
class GFG{
static double subfactorial(int N)
{
double res = 0, fact = 1;
int count = 0;
for (int i = 1; i <= N; i++) {
fact = fact * i;
if (count % 2 == 0)
res = res - (1 / fact);
else
res = res + (1 / fact);
count++;
}
return fact * (1 + res);
}
public static void Main()
{
int N = 4;
Console.Write(subfactorial(N));
}
}
|
Javascript
<script>
function subfactorial(N) {
let res = 0, fact = 1;
let count = 0;
for (let i = 1; i <= N; i++) {
fact = fact * i;
if (count % 2 == 0)
res = res - 1 / fact;
else
res = res + 1 / fact;
count++;
}
return fact * (1 + res);
}
let N = 4;
document.write(subfactorial(N));
</script>
|
Time Complexity: O(N)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...