Gamma Distribution Model in Mathematics
Last Updated :
21 Jan, 2021
Introduction :
Suppose an event can occur several times within a given unit of time. When the total number of occurrences of the event is unknown, we can think of it as a random variable. Now, if this random variable X has gamma distribution, then its probability density function is given as follows.
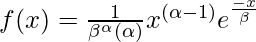
only when x > 0, α >0, β >0. Otherwise f(x) = 0
where, Γ(α) is the value of the gamma function, defined by :
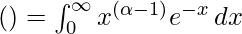
Integrating it by parts, we get that :
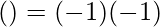 for α > 1
for α > 1
Thus, Γ(α) = (α-1)! When α is a positive integer.
Represented as –
X ~ GAM(β, α)
Expected Value :
The Expected Value of the Poisson distribution can be found by summing up products of Values with their respective probabilities.
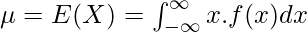
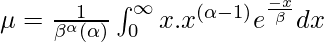
After putting y = x/β, we get –

Now, after using the identity, Γ(α + 1) = α · Γ(α), we get –
μ = α β
Variance and Standard Deviation :
The Variance of the Gamma distribution can be found using the Variance Formula.
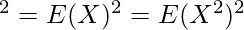
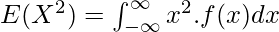

After putting y = x/β, we get –
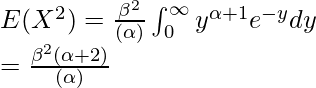
But, Γ(α + 2) = (α+1) · Γ(α+1) and Γ(α+1) = α · Γ(α)
=> Γ(α + 2) = α.(α+1).Γ(α), we get –
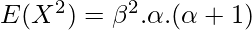
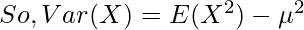
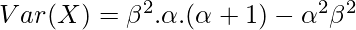
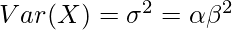
Standard Deviation is given by –
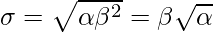
Note –
In special case if α = 1, we get exponential distribution with 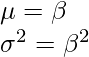
Share your thoughts in the comments
Please Login to comment...