Python – Central Limit Theorem

Statistics is an important part of Data science projects. We use statical tools whenever we want to make any inference about the population of the dataset from a sample of the dataset, gather information from the dataset, or make any assumption about the parameter of the dataset. In this article, we will talk about one of the important statical tools central limit theorem.

What is Central Limit Theorem 

The definition: 

The central limit theoram states that if we take large number of samples from any population with finite mean and variance then the distribution of the sample means will follow the normal distribution regradless of the type of the original distribution. Also the mean of these sample means will be equal to the population mean and standard error(standard deviation of the sample means) will decrease with increase in sample size.

Central limit theoram 

Suppose we are sampling from a population with a finite mean and a finite standard deviation (sigma). Then Mean and standard deviation of the sampling distribution of the sample mean can be given as: 
\qquad \qquad \mu_{\bar{X}}=\mu \qquad \sigma_{\bar{X}}=\frac{\sigma}{\sqrt{n}}   

Where 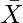   represents the sampling distribution of the sample mean of size n each,  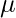  and    are the mean and standard deviation of the population respectively. 
The distribution of the sample tends towards the normal distribution as the sample size increases.

Use of Central Limit Theorem(CLT)

We can use central limit theorem for various purposes in data science project some the key uses are listed below

• Population Parameter Estimation – We can use CLT to estimate the parameters of the population like population mean or population proportion based on a sampled data. 
• Hypothesis testing –  CLT can be used for various hypothesis assumptions tests as It helps in constructing test statistics, such as the z-test or t-test, by assuming that the sampling distribution of the test statistic is approximately normal.
• Confidence interval – Confidence interval plays a very important role in defing the range in which the population parameter lies. CLT plays a very crucial role in determining the confidence interval of these population parameter.
• Sampling Techniques – sampling technique help in collecting representative samples and generalize the findings to the larger population. The CLT supports various sampling techniques used in survey sampling and experimental design.
• Simultion and Monte Carlo Methods – This methods involve generating random samples from known distributions to approximate the behavior of complex systems or estimate statistical quantities. CLT plays a very key role in the simulation and monte carlo methods.

Python Implementation of The Central Limit Theorem

We will generate random numbers from -40 to 40 and and collect their mean in a list. we will itratively perform his operation for different count of numbers and we will plot their sampling distribution. 

python3

import numpy
import matplotlib.pyplot as plt

# number of sample
num = [1, 10, 50, 100]
# list of sample means
means = []

# Generating 1, 10, 30, 100 random numbers from -40 to 40
# taking their mean and appending it to list means.
for j in num:
    # Generating seed so that we can get same result
    # every time the loop is run...
    numpy.random.seed(1)
    x = [numpy.mean(
        numpy.random.randint(
            -40, 40, j)) for _i in range(1000)]
    means.append(x)
k = 0

# plotting all the means in one figure
fig, ax = plt.subplots(2, 2, figsize =(8, 8))
for i in range(0, 2):
    for j in range(0, 2):
        # Histogram for each x stored in means
        ax[i, j].hist(means[k], 10, density = True)
        ax[i, j].set_title(label = num[k])
        k = k + 1
 plt.show()

Output:

Central limit theoram for getting normal distribution 

It is evident from the graphs that as we keep on increasing the sample size from 1 to 100 the histogram tends to take the shape of a normal distribution.

Rule of Thumb For Central Limit Theoram 

Generally, the Central Limit Theoram is used when the sample size is fairly big, usually larger than or equal to 30. In some cases even if the sample size is less than 30 central limit theoram still holds but for this the population distribution should be close to normal or symmetric.