Lagrange’s Interpolation

What is Interpolation?
Interpolation is a method of finding new data points within the range of a discrete set of known data points (Source Wiki). In other words interpolation is the technique to estimate the value of a mathematical function, for any intermediate value of the independent variable. 
For example, in the given table we’re given 4 set of discrete data points, for an unknown function f(x) :

How to find?
Here we can apply the Lagrange’s interpolation formula to get our solution. 
The Lagrange’s Interpolation formula: 
If, y = f(x) takes the values y0, y1, … , yn corresponding to x = x0, x1 , … , xn then,

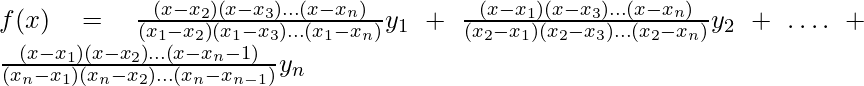
This method is preferred over its counterparts like Newton’s method because it is applicable even for unequally spaced values of x.
We can use interpolation techniques to find an intermediate data point say at x = 3. 

Advantages of Lagrange Interpolation:

• This formula is used to find the value of the function even when the arguments are not equally spaced.
• This formula is used to find the value of independent variable x corresponding to a given value of a function.

Disadvantages of Lagrange Interpolation:

• A change of degree in Lagrangian polynomial involves a completely new computation of all the terms.
• For a polynomial of high degree, the formula involves a large number of multiplications which make the process quite slow.
• In the Lagrange Interpolation, the degree of polynomial is chosen at the outset. So it is difficult to find the degree of approximating polynomial which is suitable for given set of tabulated points.

C++

// C++ program for implementation of Lagrange's Interpolation
#include<bits/stdc++.h>
using namespace std;

// To represent a data point corresponding to x and y = f(x)
struct Data
{
    int x, y;
};

// function to interpolate the given data points using Lagrange's formula
// xi corresponds to the new data point whose value is to be obtained
// n represents the number of known data points
double interpolate(Data f[], int xi, int n)
{
    double result = 0; // Initialize result

    for (int i=0; i<n; i++)
    {
        // Compute individual terms of above formula
        double term = f[i].y;
        for (int j=0;j<n;j++)
        {
            if (j!=i)
                term = term*(xi - f[j].x)/double(f[i].x - f[j].x);
        }

        // Add current term to result
        result += term;
    }

    return result;
}

// driver function to check the program
int main()
{
    // creating an array of 4 known data points
    Data f[] = {{0,2}, {1,3}, {2,12}, {5,147}};

    // Using the interpolate function to obtain a data point
    // corresponding to x=3
    cout << "Value of f(3) is : " << interpolate(f, 3, 4);

    return 0;
}

Java

// Java program for implementation
// of Lagrange's Interpolation

import java.util.*;

class GFG
{

// To represent a data point
// corresponding to x and y = f(x)
static class Data
{
    int x, y;

    public Data(int x, int y)
    {
        super();
        this.x = x;
        this.y = y;
    }

};

// function to interpolate the given
// data points using Lagrange's formula
// xi corresponds to the new data point
// whose value is to be obtained n
// represents the number of known data points
static double interpolate(Data f[], int xi, int n)
{
    double result = 0; // Initialize result

    for (int i = 0; i < n; i++)
    {
        // Compute individual terms of above formula
        double term = f[i].y;
        for (int j = 0; j < n; j++)
        {
            if (j != i)
                term = term*(xi - f[j].x) / (f[i].x - f[j].x);
        }

        // Add current term to result
        result += term;
    }

    return result;
}

// Driver code
public static void main(String[] args)
{
    // creating an array of 4 known data points
    Data f[] = {new Data(0, 2), new Data(1, 3),
                new Data(2, 12), new Data(5, 147)};

    // Using the interpolate function to obtain
    // a data point corresponding to x=3
    System.out.print("Value of f(3) is : " +
                    (int)interpolate(f, 3, 4));
}
}

// This code is contributed by 29AjayKumar

Python3

# Python3 program for implementation
# of Lagrange's Interpolation

# To represent a data point corresponding to x and y = f(x)
class Data:
    def __init__(self, x, y):
        self.x = x
        self.y = y

# function to interpolate the given data points
# using Lagrange's formula
# xi -> corresponds to the new data point
# whose value is to be obtained
# n -> represents the number of known data points
def interpolate(f: list, xi: int, n: int) -> float:

    # Initialize result
    result = 0.0
    for i in range(n):

        # Compute individual terms of above formula
        term = f[i].y
        for j in range(n):
            if j != i:
                term = term * (xi - f[j].x) / (f[i].x - f[j].x)

        # Add current term to result
        result += term

    return result

# Driver Code
if __name__ == "__main__":

    # creating an array of 4 known data points
    f = [Data(0, 2), Data(1, 3), Data(2, 12), Data(5, 147)]

    # Using the interpolate function to obtain a data point
    # corresponding to x=3
    print("Value of f(3) is :", interpolate(f, 3, 4))

# This code is contributed by
# sanjeev2552

C#

// C# program for implementation
// of Lagrange's Interpolation
using System;

class GFG
{

// To represent a data point
// corresponding to x and y = f(x)
class Data
{
    public int x, y;
    public Data(int x, int y)
    {
        this.x = x;
        this.y = y;
    }
};

// function to interpolate the given
// data points using Lagrange's formula
// xi corresponds to the new data point
// whose value is to be obtained n
// represents the number of known data points
static double interpolate(Data []f,
                          int xi, int n)
{
    double result = 0; // Initialize result

    for (int i = 0; i < n; i++)
    {
        // Compute individual terms
        // of above formula
        double term = f[i].y;
        for (int j = 0; j < n; j++)
        {
            if (j != i)
                term = term * (xi - f[j].x) /
                          (f[i].x - f[j].x);
        }

        // Add current term to result
        result += term;
    }
    return result;
}

// Driver code
public static void Main(String[] args)
{
    // creating an array of 4 known data points
    Data []f = {new Data(0, 2),
                new Data(1, 3),
                new Data(2, 12),
                new Data(5, 147)};

    // Using the interpolate function to obtain
    // a data point corresponding to x=3
    Console.Write("Value of f(3) is : " +
                  (int)interpolate(f, 3, 4));
}
}

// This code is contributed by PrinciRaj1992

Javascript

<script>
// Javascript program for implementation
// of Lagrange's Interpolation

// To represent a data point
// corresponding to x and y = f(x)
class Data
{
    constructor(x,y)
    {
        this.x=x;
        this.y=y;
    }
}

// function to interpolate the given
// data points using Lagrange's formula
// xi corresponds to the new data point
// whose value is to be obtained n
// represents the number of known data points
function interpolate(f,xi,n)
{
    let result = 0; // Initialize result

    for (let i = 0; i < n; i++)
    {
        // Compute individual terms of above formula
        let term = f[i].y;
        for (let j = 0; j < n; j++)
        {
            if (j != i)
                term = term*(xi - f[j].x) / (f[i].x - f[j].x);
        }

        // Add current term to result
        result += term;
    }

    return result;
}

// Driver code
 // creating an array of 4 known data points
let f=[new Data(0, 2), new Data(1, 3),
                new Data(2, 12), new Data(5, 147)];

// Using the interpolate function to obtain
    // a data point corresponding to x=3
document.write("Value of f(3) is : " +
                    interpolate(f, 3, 4));


// This code is contributed by rag2127
</script>

Output:

Value of f(3) is : 35

Complexity:
The time complexity of the above solution is O(n²) and auxiliary space is O(1).

References:

• https://en.wikipedia.org/wiki/Lagrange_polynomial
  Higher Engineering Mathematics , Dr. B.S. Grewal
• https://mat.iitm.ac.in/home/sryedida/public_html/caimna/interpolation/lagrange.html

Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.