Ordinary Least Squares (OLS) using statsmodels
Last Updated :
10 Mar, 2022
In this article, we will use Python’s statsmodels module to implement Ordinary Least Squares(OLS) method of linear regression.
Introduction :
A linear regression model establishes the relation between a dependent variable(y) and at least one independent variable(x) as :
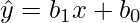
In OLS method, we have to choose the values of 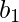 and
and 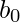 such that, the total sum of squares of the difference between the calculated and observed values of y, is minimised.
such that, the total sum of squares of the difference between the calculated and observed values of y, is minimised.
Formula for OLS:
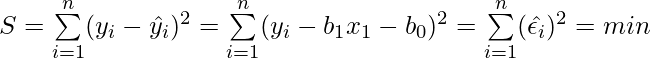
Where,
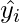 = predicted value for the ith observation
= predicted value for the ith observation
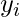 = actual value for the ith observation
= actual value for the ith observation
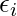 = error/residual for the ith observation
= error/residual for the ith observation
n = total number of observations
To get the values of 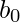 and
and 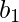 which minimise S, we can take a partial derivative for each coefficient and equate it to zero.
which minimise S, we can take a partial derivative for each coefficient and equate it to zero.
Modules used :
- statsmodels : provides classes and functions for the estimation of many different statistical models.
pip install statsmodels
pandas : library used for data manipulation and analysis.
NumPy : core library for array computing.
Matplotlib : a comprehensive library used for creating static and interactive graphs and visualisations.
Approach :
- First we define the variables x and y. In the example below, the variables are read from a csv file using pandas. The file used in the example can be downloaded here.
- Next, We need to add the constant
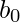 to the equation using the add_constant() method.
to the equation using the add_constant() method. - The OLS() function of the statsmodels.api module is used to perform OLS regression. It returns an OLS object. Then fit() method is called on this object for fitting the regression line to the data.
- The summary() method is used to obtain a table which gives an extensive description about the regression results
Syntax : statsmodels.api.OLS(y, x)
Parameters :
- y : the variable which is dependent on x
- x : the independent variable
Code:
Python3
import statsmodels.api as sm
import pandas as pd
data = pd.read_csv('train.csv')
x = data['x'].tolist()
y = data['y'].tolist()
x = sm.add_constant(x)
result = sm.OLS(y, x).fit()
print(result.summary())
|
Output :
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.989
Model: OLS Adj. R-squared: 0.989
Method: Least Squares F-statistic: 2.709e+04
Date: Fri, 26 Jun 2020 Prob (F-statistic): 1.33e-294
Time: 15:55:38 Log-Likelihood: -757.98
No. Observations: 300 AIC: 1520.
Df Residuals: 298 BIC: 1527.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const -0.4618 0.360 -1.284 0.200 -1.169 0.246
x1 1.0143 0.006 164.598 0.000 1.002 1.026
==============================================================================
Omnibus: 1.034 Durbin-Watson: 2.006
Prob(Omnibus): 0.596 Jarque-Bera (JB): 0.825
Skew: 0.117 Prob(JB): 0.662
Kurtosis: 3.104 Cond. No. 120.
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Description of some of the terms in the table :
- R-squared : the coefficient of determination. It is the proportion of the variance in the dependent variable that is predictable/explained
- Adj. R-squared : Adjusted R-squared is the modified form of R-squared adjusted for the number of independent variables in the model. Value of adj. R-squared increases, when we include extra variables which actually improve the model.
- F-statistic : the ratio of mean squared error of the model to the mean squared error of residuals. It determines the overall significance of the model.
- coef : the coefficients of the independent variables and the constant term in the equation.
- t : the value of t-statistic. It is the ratio of the difference between the estimated and hypothesized value of a parameter, to the standard error
Predicting values:
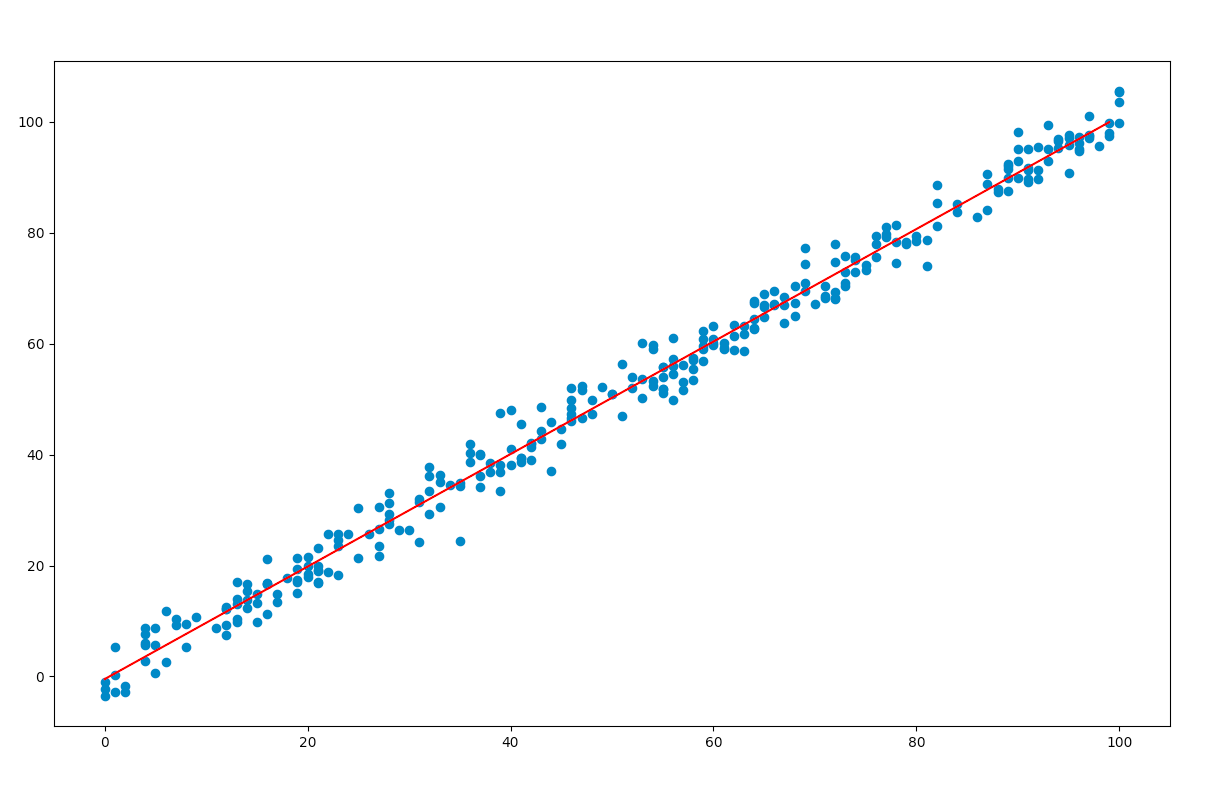
From the results table, we note the coefficient of x and the constant term. These values are substituted in the original equation and the regression line is plotted using matplotlib.
Code:
Python3
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
data = pd.read_csv('train.csv')
x = data['x'].tolist()
y = data['y'].tolist()
plt.scatter(x, y)
max_x = data['x'].max()
min_x = data['x'].min()
x = np.arange(min_x, max_x, 1)
y = 1.0143 * x - 0.4618
plt.plot(y, 'r')
plt.show()
|
Output:
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...