Mathematics | Reimann Zeta Distribution Model
Last Updated :
19 Feb, 2021
Introduction :
Suppose an event can occur several times within a given unit of time. When the total number of occurrences of the event is unknown, we can think of it as a random variable. When a random variable X takes on values on discrete time interval from 1 to infinity, one choice of a probability density is the Reimann Zeta distribution whose probability density function is given by as follows.
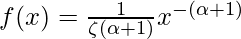
Above expression will be applicable only when given below condition will follow.
x = 1,2,3,.... .
f(x) = 0, Otherwise
.
f(x) = 0, Otherwise
Where, 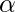 is the parameter and
is the parameter and 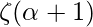 is the value of the zeta function, defined by as follows.
is the value of the zeta function, defined by as follows.
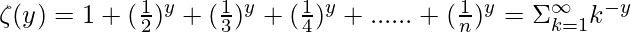
The random variable X following Reimann Zeta Distribution is represented as follows.
X ~ RIE(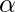 )
)
Expected Value :
The Expected Value of the Reimann Zeta distribution can be found by summing up products of Values with their respective probabilities as follows.
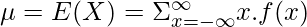
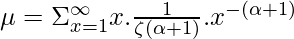
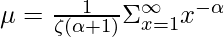
Using the property 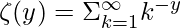 , we get the following expression as follows.
, we get the following expression as follows.

Variance and Standard Deviation :
The Variance of the Riemann Zeta distribution can be found using the Variance Formula as follows.
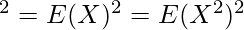
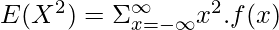
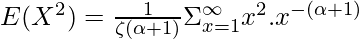
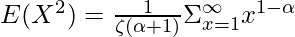
Using the property 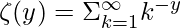 , we get the following expression as follows.
, we get the following expression as follows.
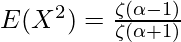
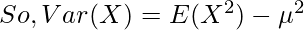
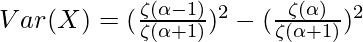
![Rendered by QuickLaTeX.com Var(X) = \sigma^2 = \frac{[\zeta(\alpha-1)]^2 - [\zeta(\alpha)]^2}{[\zeta(\alpha+1)]^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a1fadf9a20bba1c80fc9430625d6091f_l3.png)
Standard Deviation is given by as follows.
![Rendered by QuickLaTeX.com \sigma = \frac{1}{\zeta(\alpha+1)} \sqrt{[\zeta(\alpha-1)]^2 - [\zeta(\alpha)]^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-73de424a344b8fa423e003d67cfe863f_l3.png)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...