Mathematics | Covariance and Correlation

Covariance and Correlation are two mathematical concepts which are commonly used in the field of probability and statistics. Both concepts describe the relationship between two variables.

Covariance –

1. It is the relationship between a pair of random variables where change in one variable causes change in another variable.
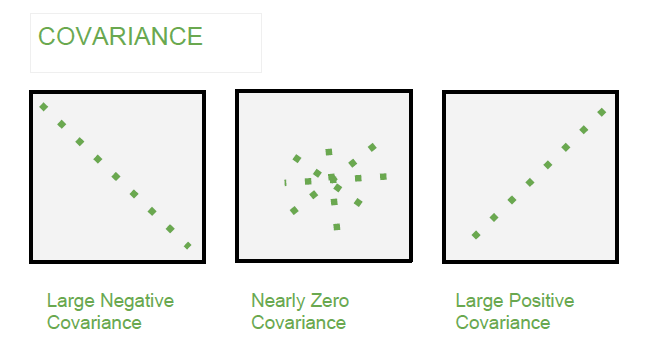
2. It can take any value between -infinity to +infinity, where the negative value represents the negative relationship whereas a positive value represents the positive relationship.
3. It is used for the linear relationship between variables.
4. It gives the direction of relationship between variables.

Formula –
For Population:

For Sample

Here,
x’ and y’ = mean of given sample set
n = total no of sample
xi and yi = individual sample of set

Example –

Correlation –

1. It show whether and how strongly pairs of variables are related to each other.
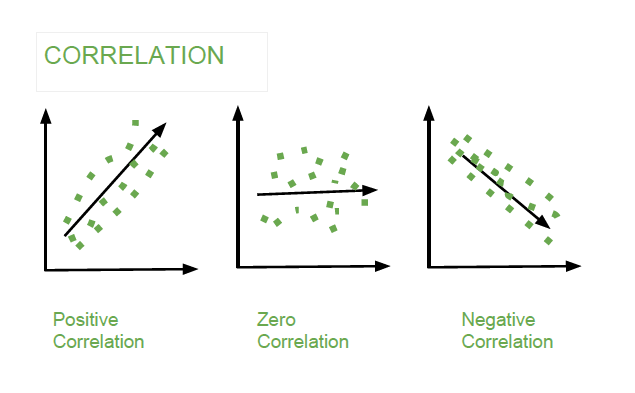
2. Correlation takes values between -1 to +1, wherein values close to +1 represents strong positive correlation and values close to -1 represents strong negative correlation.
3. In this variable are indirectly related to each other.
4. It gives the direction and strength of relationship between variables.

Formula –

Here,
x’ and y’ = mean of given sample set
n = total no of sample
xi and yi = individual sample of set

Example –

Covariance versus Correlation –

Covariance	Correlation
Covariance is a measure of how much two random variables vary together	Correlation is a statistical measure that indicates how strongly two variables are related.
involve the relationship between two variables or data sets	involve the relationship between multiple variables as well
Lie between -infinity and +infinity	Lie between -1 and +1
Measure of correlation	Scaled version of covariance
provide direction of relationship	provide direction and strength of relationship
dependent on scale of variable	independent on scale of variable
have dimensions	dimensionless