Mathematics | Beta Distribution Model
Last Updated :
18 Feb, 2021
Introduction :
Suppose an event can occur several times within a given unit of time. When the total number of occurrences of the event is unknown, we can think of it as a random variable. When a random variable X takes on values on the interval from 0 to 1, one choice of a probability density is the beta distribution whose probability density function is given by as follows.
Representation of probability density function –
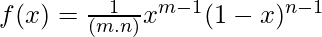
It will be applicable only when the given below given condition will pass.
x > 0, m >0, n >0.
f(x) = 0 , Otherwise
Here, you will see the meaning of function as you have shown in representation of probability density function where, B(m.n) is the value of the beta function.
Representation of B(m.n) –
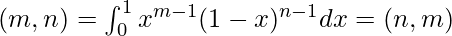
Integrating it by parts, we will get the following expression as given below.
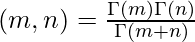
Where, Γ(x) is the gamma function of x, calculated as –
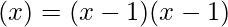 for x>1
for x>1
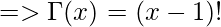 when x is an integer
when x is an integer
The random variable X is represented as follows.
Representation of random variable X –
X ~ BETA(m,n)
Expected Value:
The Expected Value of the Beta distribution can be found by summing up products of Values with their respective probabilities.
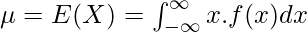
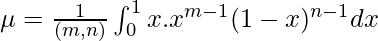

Upon using the value of beta function, we will get the following expression a follows.

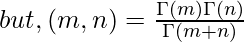
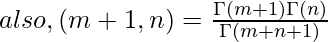

Upon using the property of gamma function, that is Γ(x) = (x-1)!, we will get the following expression as follows.
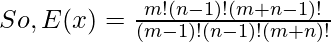 here, m, n -> integers
here, m, n -> integers
 where provided m and n are integers.
where provided m and n are integers.
Variance and Standard Deviation :
The Variance of the Beta distribution can be found using the Variance Formula.
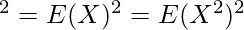
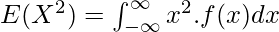

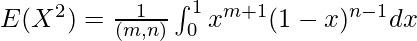
Upon using the value of beta function, we will get the following expression as follows.
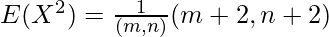
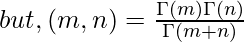
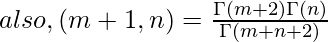
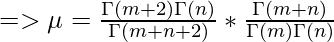
Upon using the property of gamma function, that is Γ(x) = (x-1)!, we will get the following expression as follows.
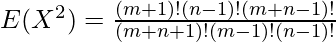
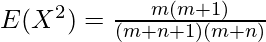
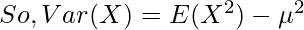
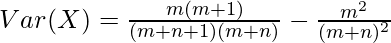
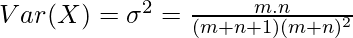
Standard Deviation is given by as follows.
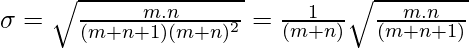
Example –
In a certain county, the proportion of highway sections requiring repairs in any given year is a random variable having the beta distribution with m = 3 and n = 2.
(a) On the average, what percentage of the highway sections require repairs in any given year?
(b) Find the probability that at most half of the highway sections will require repairs in any given year.
Solution –
(a) 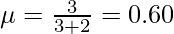
which means that on the average 60% of the highway sections require repairs in any given year.
(b) Substituting m=3 and n=2 in the probability density function, and
using Γ(3) = 2! = 2, Γ(2) = 1! = 1, Γ(5) = 4! = 24,
we will get the following expression as follows.
f(x) = 12 x^2 (1 − x) for 0<x<1. Otherwise f(x) = 0
Thus, the desired probability is given by as follows.
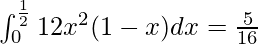
Share your thoughts in the comments
Please Login to comment...