Hypothesis testing involves formulating assumptions about population parameters based on sample statistics and rigorously evaluating these assumptions against empirical evidence. This article sheds light on the significance of hypothesis testing and the critical steps involved in the process.
What is Hypothesis Testing?
Hypothesis testing is a statistical method that is used to make a statistical decision using experimental data. Hypothesis testing is basically an assumption that we make about a population parameter. It evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data.
Example: You say an average height in the class is 30 or a boy is taller than a girl. All of these is an assumption that we are assuming, and we need some statistical way to prove these. We need some mathematical conclusion whatever we are assuming is true.
Defining Hypotheses
- Null hypothesis (H0): In statistics, the null hypothesis is a general statement or default position that there is no relationship between two measured cases or no relationship among groups. In other words, it is a basic assumption or made based on the problem knowledge.
Example: A company’s mean production is 50 units/per da H0:  = 50.
= 50. - Alternative hypothesis (H1): The alternative hypothesis is the hypothesis used in hypothesis testing that is contrary to the null hypothesis.
Example: A company’s production is not equal to 50 units/per day i.e. H1: 
 50.
50.
Key Terms of Hypothesis Testing
- Level of significance: It refers to the degree of significance in which we accept or reject the null hypothesis. 100% accuracy is not possible for accepting a hypothesis, so we, therefore, select a level of significance that is usually 5%. This is normally denoted with
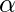 and generally, it is 0.05 or 5%, which means your output should be 95% confident to give a similar kind of result in each sample.
and generally, it is 0.05 or 5%, which means your output should be 95% confident to give a similar kind of result in each sample. - P-value: The P value, or calculated probability, is the probability of finding the observed/extreme results when the null hypothesis(H0) of a study-given problem is true. If your P-value is less than the chosen significance level then you reject the null hypothesis i.e. accept that your sample claims to support the alternative hypothesis.
- Test Statistic: The test statistic is a numerical value calculated from sample data during a hypothesis test, used to determine whether to reject the null hypothesis. It is compared to a critical value or p-value to make decisions about the statistical significance of the observed results.
- Critical value: The critical value in statistics is a threshold or cutoff point used to determine whether to reject the null hypothesis in a hypothesis test.
- Degrees of freedom: Degrees of freedom are associated with the variability or freedom one has in estimating a parameter. The degrees of freedom are related to the sample size and determine the shape.
Why do we use Hypothesis Testing?
Hypothesis testing is an important procedure in statistics. Hypothesis testing evaluates two mutually exclusive population statements to determine which statement is most supported by sample data. When we say that the findings are statistically significant, thanks to hypothesis testing.
One-Tailed and Two-Tailed Test
One tailed test focuses on one direction, either greater than or less than a specified value. We use a one-tailed test when there is a clear directional expectation based on prior knowledge or theory. The critical region is located on only one side of the distribution curve. If the sample falls into this critical region, the null hypothesis is rejected in favor of the alternative hypothesis.
One-Tailed Test
There are two types of one-tailed test:
- Left-Tailed (Left-Sided) Test: The alternative hypothesis asserts that the true parameter value is less than the null hypothesis. Example: H0:
 and H1:
and H1: 
- Right-Tailed (Right-Sided) Test: The alternative hypothesis asserts that the true parameter value is greater than the null hypothesis. Example: H0 :
 and H1:
and H1:
Two-Tailed Test
A two-tailed test considers both directions, greater than and less than a specified value.We use a two-tailed test when there is no specific directional expectation, and want to detect any significant difference.
Example: H0:  50 and H1:
50 and H1: 
What are Type 1 and Type 2 errors in Hypothesis Testing?
In hypothesis testing, Type I and Type II errors are two possible errors that researchers can make when drawing conclusions about a population based on a sample of data. These errors are associated with the decisions made regarding the null hypothesis and the alternative hypothesis.
- Type I error: When we reject the null hypothesis, although that hypothesis was true. Type I error is denoted by alpha(
 ).
). - Type II errors: When we accept the null hypothesis, but it is false. Type II errors are denoted by beta(
 ).
).
|
Correct Decision
| Type II Error (False Negative)
|
Type I Error (False Positive)
| Correct Decision
|
How does Hypothesis Testing work?
Step 1: Define Null and Alternative Hypothesis
State the null hypothesis ( ), representing no effect, and the alternative hypothesis (
), representing no effect, and the alternative hypothesis ( ), suggesting an effect or difference.
), suggesting an effect or difference.
We first identify the problem about which we want to make an assumption keeping in mind that our assumption should be contradictory to one another, assuming Normally distributed data.
Step 2 – Choose significance level
Select a significance level ( ), typically 0.05, to determine the threshold for rejecting the null hypothesis. It provides validity to our hypothesis test, ensuring that we have sufficient data to back up our claims. Usually, we determine our significance level beforehand of the test. The p-value is the criterion used to calculate our significance value.
), typically 0.05, to determine the threshold for rejecting the null hypothesis. It provides validity to our hypothesis test, ensuring that we have sufficient data to back up our claims. Usually, we determine our significance level beforehand of the test. The p-value is the criterion used to calculate our significance value.
Step 3 – Collect and Analyze data.
Gather relevant data through observation or experimentation. Analyze the data using appropriate statistical methods to obtain a test statistic.
Step 4-Calculate Test Statistic
The data for the tests are evaluated in this step we look for various scores based on the characteristics of data. The choice of the test statistic depends on the type of hypothesis test being conducted.
There are various hypothesis tests, each appropriate for various goal to calculate our test. This could be a Z-test, Chi-square, T-test, and so on.
- Z-test: If population means and standard deviations are known. Z-statistic is commonly used.
- t-test: If population standard deviations are unknown. and sample size is small than t-test statistic is more appropriate.
- Chi-square test: Chi-square test is used for categorical data or for testing independence in contingency tables
- F-test: F-test is often used in analysis of variance (ANOVA) to compare variances or test the equality of means across multiple groups.
We have a smaller dataset, So, T-test is more appropriate to test our hypothesis.
T-statistic is a measure of the difference between the means of two groups relative to the variability within each group. It is calculated as the difference between the sample means divided by the standard error of the difference. It is also known as the t-value or t-score.
Step 5 – Comparing Test Statistic:
In this stage, we decide where we should accept the null hypothesis or reject the null hypothesis. There are two ways to decide where we should accept or reject the null hypothesis.
Method A: Using Crtical values
Comparing the test statistic and tabulated critical value we have,
- If Test Statistic>Critical Value: Reject the null hypothesis.
- If Test Statistic≤Critical Value: Fail to reject the null hypothesis.
Note: Critical values are predetermined threshold values that are used to make a decision in hypothesis testing. To determine critical values for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.
Method B: Using P-values
We can also come to an conclusion using the p-value,
- If the p-value is less than or equal to the significance level i.e. (
 ), you reject the null hypothesis. This indicates that the observed results are unlikely to have occurred by chance alone, providing evidence in favor of the alternative hypothesis.
), you reject the null hypothesis. This indicates that the observed results are unlikely to have occurred by chance alone, providing evidence in favor of the alternative hypothesis. - If the p-value is greater than the significance level i.e. (
 ), you fail to reject the null hypothesis. This suggests that the observed results are consistent with what would be expected under the null hypothesis.
), you fail to reject the null hypothesis. This suggests that the observed results are consistent with what would be expected under the null hypothesis.
Note: The p-value is the probability of obtaining a test statistic as extreme as, or more extreme than, the one observed in the sample, assuming the null hypothesis is true. To determine p-value for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.
Step 7- Interpret the Results
At last, we can conclude our experiment using method A or B.
Calculating test statistic
To validate our hypothesis about a population parameter we use statistical functions. We use the z-score, p-value, and level of significance(alpha) to make evidence for our hypothesis for normally distributed data.
1. Z-statistics:
When population means and standard deviations are known.

where,
 is the sample mean,
is the sample mean,- μ represents the population mean,
- σ is the standard deviation
- and n is the size of the sample.
2. T-Statistics
T test is used when n<30,
t-statistic calculation is given by:

where,
- t = t-score,
- x̄ = sample mean
- μ = population mean,
- s = standard deviation of the sample,
- n = sample size
3. Chi-Square Test
Chi-Square Test for Independence categorical Data (Non-normally distributed) using:

where,
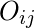 is the observed frequency in cell
is the observed frequency in cell 
- i,j are the rows and columns index respectively.
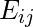 is the expected frequency in cell
is the expected frequency in cell  , calculated as :
, calculated as :

Real life Hypothesis Testing example
Let’s examine hypothesis testing using two real life situations,
Case A: Does a New Drug Affect Blood Pressure?
Imagine a pharmaceutical company has developed a new drug that they believe can effectively lower blood pressure in patients with hypertension. Before bringing the drug to market, they need to conduct a study to assess its impact on blood pressure.
Data:
- Before Treatment: 120, 122, 118, 130, 125, 128, 115, 121, 123, 119
- After Treatment: 115, 120, 112, 128, 122, 125, 110, 117, 119, 114
Step 1: Define the Hypothesis
- Null Hypothesis: (H0)The new drug has no effect on blood pressure.
- Alternate Hypothesis: (H1)The new drug has an effect on blood pressure.
Step 2: Define the Significance level
Let’s consider the Significance level at 0.05, indicating rejection of the null hypothesis.
If the evidence suggests less than a 5% chance of observing the results due to random variation.
Step 3: Compute the test statistic
Using paired T-test analyze the data to obtain a test statistic and a p-value.
The test statistic (e.g., T-statistic) is calculated based on the differences between blood pressure measurements before and after treatment.
t = m/(s/√n)
Where:
- m = mean of the difference i.e Xafter, Xbefore
- s = standard deviation of the difference (d) i.e di=Xafter,i−Xbefore,
- n = sample size,
then, m= -3.9, s= 1.8 and n= 10
we, calculate the , T-statistic = -9 based on the formula for paired t test
Step 4: Find the p-value
The calculated t-statistic is -9 and degrees of freedom df = 9, you can find the p-value using statistical software or a t-distribution table.
thus, p-value = 8.538051223166285e-06
Step 5: Result
- If the p-value is less than or equal to 0.05, the researchers reject the null hypothesis.
- If the p-value is greater than 0.05, they fail to reject the null hypothesis.
Conclusion: Since the p-value (8.538051223166285e-06) is less than the significance level (0.05), the researchers reject the null hypothesis. There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different.
Python Implementation of Hypothesis Testing
Let’s create hypothesis testing with python, where we are testing whether a new drug affects blood pressure. For this example, we will use a paired T-test. We’ll use the scipy.stats library for the T-test.
Scipy is a mathematical library in Python that is mostly used for mathematical equations and computations.
We will implement our first real life problem via python,
Python3
import numpy as np
from scipy import stats
before_treatment = np.array([120, 122, 118, 130, 125, 128, 115, 121, 123, 119])
after_treatment = np.array([115, 120, 112, 128, 122, 125, 110, 117, 119, 114])
null_hypothesis = "The new drug has no effect on blood pressure."
alternate_hypothesis = "The new drug has an effect on blood pressure."
alpha = 0.05
t_statistic, p_value = stats.ttest_rel(after_treatment, before_treatment)
m = np.mean(after_treatment - before_treatment)
s = np.std(after_treatment - before_treatment, ddof=1)
n = len(before_treatment)
t_statistic_manual = m / (s / np.sqrt(n))
if p_value <= alpha:
decision = "Reject"
else:
decision = "Fail to reject"
if decision == "Reject":
conclusion = "There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different."
else:
conclusion = "There is insufficient evidence to claim a significant difference in average blood pressure before and after treatment with the new drug."
print("T-statistic (from scipy):", t_statistic)
print("P-value (from scipy):", p_value)
print("T-statistic (calculated manually):", t_statistic_manual)
print(f"Decision: {decision} the null hypothesis at alpha={alpha}.")
print("Conclusion:", conclusion)
|
Output:
T-statistic (from scipy): -9.0
P-value (from scipy): 8.538051223166285e-06
T-statistic (calculated manually): -9.0
Decision: Reject the null hypothesis at alpha=0.05.
Conclusion: There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different.
In the above example, given the T-statistic of approximately -9 and an extremely small p-value, the results indicate a strong case to reject the null hypothesis at a significance level of 0.05.
- The results suggest that the new drug, treatment, or intervention has a significant effect on lowering blood pressure.
- The negative T-statistic indicates that the mean blood pressure after treatment is significantly lower than the assumed population mean before treatment.
Case B: Cholesterol level in a population
Data: A sample of 25 individuals is taken, and their cholesterol levels are measured.
Cholesterol Levels (mg/dL): 205, 198, 210, 190, 215, 205, 200, 192, 198, 205, 198, 202, 208, 200, 205, 198, 205, 210, 192, 205, 198, 205, 210, 192, 205.
Populations Mean = 200
Population Standard Deviation (σ): 5 mg/dL(given for this problem)
Step 1: Define the Hypothesis
- Null Hypothesis (H0): The average cholesterol level in a population is 200 mg/dL.
- Alternate Hypothesis (H1): The average cholesterol level in a population is different from 200 mg/dL.
Step 2: Define the Significance level
As the direction of deviation is not given , we assume a two-tailed test, and based on a normal distribution table, the critical values for a significance level of 0.05 (two-tailed) can be calculated through the z-table and are approximately -1.96 and 1.96.
Step 3: Compute the test statistic
The test statistic is calculated by using the z formula Z= and we get accordingly , Z=2.039999999999992.
and we get accordingly , Z=2.039999999999992.
Step 4: Result
Since the absolute value of the test statistic (2.04) is greater than the critical value (1.96), we reject the null hypothesis. And conclude that, there is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL
Python Implementation of Hypothesis Testing
Python3
import scipy.stats as stats
import math
import numpy as np
sample_data = np.array(
[205, 198, 210, 190, 215, 205, 200, 192, 198, 205, 198, 202, 208, 200, 205, 198, 205, 210, 192, 205, 198, 205, 210, 192, 205])
population_std_dev = 5
population_mean = 200
sample_size = len(sample_data)
alpha = 0.05
critical_value_left = stats.norm.ppf(alpha/2)
critical_value_right = -critical_value_left
sample_mean = sample_data.mean()
z_score = (sample_mean - population_mean) / \
(population_std_dev / math.sqrt(sample_size))
if abs(z_score) > max(abs(critical_value_left), abs(critical_value_right)):
print("Reject the null hypothesis.")
print("There is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL.")
else:
print("Fail to reject the null hypothesis.")
print("There is not enough evidence to conclude that the average cholesterol level in the population is different from 200 mg/dL.")
|
Output:
Reject the null hypothesis.
There is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL.
Limitations of Hypothesis Testing
- Although a useful technique, hypothesis testing does not offer a comprehensive grasp of the topic being studied. Without fully reflecting the intricacy or whole context of the phenomena, it concentrates on certain hypotheses and statistical significance.
- The accuracy of hypothesis testing results is contingent on the quality of available data and the appropriateness of statistical methods used. Inaccurate data or poorly formulated hypotheses can lead to incorrect conclusions.
- Relying solely on hypothesis testing may cause analysts to overlook significant patterns or relationships in the data that are not captured by the specific hypotheses being tested. This limitation underscores the importance of complimenting hypothesis testing with other analytical approaches.
Conclusion
Hypothesis testing stands as a cornerstone in statistical analysis, enabling data scientists to navigate uncertainties and draw credible inferences from sample data. By systematically defining null and alternative hypotheses, choosing significance levels, and leveraging statistical tests, researchers can assess the validity of their assumptions. The article also elucidates the critical distinction between Type I and Type II errors, providing a comprehensive understanding of the nuanced decision-making process inherent in hypothesis testing. The real-life example of testing a new drug’s effect on blood pressure using a paired T-test showcases the practical application of these principles, underscoring the importance of statistical rigor in data-driven decision-making.
Frequently Asked Questions (FAQs)
1. What are the 3 types of hypothesis test?
There are three types of hypothesis tests: right-tailed, left-tailed, and two-tailed. Right-tailed tests assess if a parameter is greater, left-tailed if lesser. Two-tailed tests check for non-directional differences, greater or lesser.
2.What are the 4 components of hypothesis testing?
Null Hypothesis ( ): No effect or difference exists.
): No effect or difference exists.
Alternative Hypothesis ( ): An effect or difference exists.
): An effect or difference exists.
Significance Level ( ): Risk of rejecting null hypothesis when it’s true (Type I error).
): Risk of rejecting null hypothesis when it’s true (Type I error).
Test Statistic: Numerical value representing observed evidence against null hypothesis.
3.What is hypothesis testing in ML?
Statistical method to evaluate the performance and validity of machine learning models. Tests specific hypotheses about model behavior, like whether features influence predictions or if a model generalizes well to unseen data.
4.What is the difference between Pytest and hypothesis in Python?
Pytest purposes general testing framework for Python code while Hypothesis is a Property-based testing framework for Python, focusing on generating test cases based on specified properties of the code.
Share your thoughts in the comments
Please Login to comment...