Descriptive Statistic
Last Updated :
02 Aug, 2023
Whenever we deal with some piece of data no matter whether it is small or stored in huge databases statistics is the key that helps us to analyze this data and provide insightful points to understand the whole data without going through each of the data pieces in the complete dataset at hand. In this article, we will learn about Descriptive Statistics and how actually we can use it as a tool to explore the data we have.
What are Descriptive Statistics?
In Descriptive statistics, we are describing our data with the help of various representative methods using charts, graphs, tables, excel files, etc. In descriptive statistics, we describe our data in some manner and present it in a meaningful way so that it can be easily understood. Most of the time it is performed on small data sets and this analysis helps us a lot to predict some future trends based on the current findings. Some measures that are used to describe a data set are measures of central tendency and measures of variability or dispersion.
Types of Descriptive Statistics
Measures of Central Tendency
It represents the whole set of data by a single value. It gives us the location of the central points. There are three main measures of central tendency:
Mean
It is the sum of observations divided by the total number of observations. It is also defined as average which is the sum divided by count.
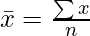
where,
- x = Observations
- n = number of terms
Let’s look at an example of how can we find the mean of a data set using Python code implementation.
Python3
import numpy as np
arr = [5, 6, 11]
mean = np.mean(arr)
print("Mean = ", mean)
|
Output :
Mean = 7.333333333333333
Mode
It is the value that has the highest frequency in the given data set. The data set may have no mode if the frequency of all data points is the same. Also, we can have more than one mode if we encounter two or more data points having the same frequency.
Python3
from scipy import stats
arr = [1, 2, 2, 3]
mode = stats.mode(arr)
print("Mode = ", mode)
|
Output:
Mode = ModeResult(mode=array([2]), count=array([2]))
Median
It is the middle value of the data set. It splits the data into two halves. If the number of elements in the data set is odd then the center element is the median and if it is even then the median would be the average of two central elements.
Python3
import numpy as np
arr = [1, 2, 3, 4]
median = np.median(arr)
print("Median = ", median)
|
Output:
Median = 2.5
Measure of Variability
Measures of variability are also termed measures of dispersion as it helps to gain insights about the dispersion or the spread of the observations at hand. Some of the measures which are used to calculate the measures of dispersion in the observations of the variables are as follows:
Range
The range describes the difference between the largest and smallest data point in our data set. The bigger the range, the more the spread of data and vice versa.
Range = Largest data value – smallest data value
Python3
import numpy as np
arr = [1, 2, 3, 4, 5]
Maximum = max(arr)
Minimum = min(arr)
Range = Maximum-Minimum
print("Maximum = {}, Minimum = {} and Range = {}".format(
Maximum, Minimum, Range))
|
Output:
Maximum = 5, Minimum = 1 and Range = 4
Variance
It is defined as an average squared deviation from the mean. It is calculated by finding the difference between every data point and the average which is also known as the mean, squaring them, adding all of them, and then dividing by the number of data points present in our data set.
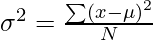
where,
- x -> Observation under consideration
- N -> number of terms
- mu -> Mean
Python3
import statistics
arr = [1, 2, 3, 4, 5]
print("Var = ", (statistics.variance(arr)))
|
Output:
Var = 2.5
Standard Deviation
It is defined as the square root of the variance. It is calculated by finding the Mean, then subtracting each number from the Mean which is also known as the average, and squaring the result. Adding all the values and then dividing by the no of terms followed by the square root.
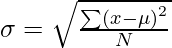
where,
- x = Observation under consideration
- N = number of terms
- mu = Mean
Python3
import statistics
arr = [1, 2, 3, 4, 5]
print("Std = ", (statistics.stdev(arr)))
|
Output:
Std = 1.5811388300841898
Measures of Frequency Distribution
Measures of frequency distribution help us gain valuable insights into the distribution and the characteristics of the dataset. Measures like,
are used to analyze the dataset on the basis of measures of frequency distribution.
Univariate v/s Bivariate
While performing the data analysis if we are considering only one variable to gain insights about it then it is known as the univariate data analysis. But if we are trying to gain insights into one variable with respect to some other variable like calculating correlation or covariance between two variables then this is known as data analysis.
Bivariate analysis helps us establish a relationship between two variables which helps us make better decisions so, that we can manipulate one to cause a positive or negative effect on the other based on the relationship between the two variables. Even though we can use multivariate data analysis to analyze and derive relationships between more than two variables these methodologies are considered to come under the domain of machine learning.
Descriptive Statistics v/s Inferential Statistics
Generally, there are two types of statistics that are used to deal with the data when the requirements of the analyst are different. The main difference lies in the final requirements only if the person just wants to extract meaningful insights from the data at hand then the domain of statistics that will be used by him is known as Descriptive Statistics but if we would like to use the observations to predict the future data let’s say in the time series related dataset then our objective contains the process of inference as well and hence it is also known as Inferential Statistics.
We can summarize this as when we would like to make some predictions/inferences based on some dataset at hand then those statistical methods are known as inferential statistics.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...