Mathematics | Hypergeometric Distribution model
Last Updated :
09 Jan, 2024
Hypergeometric Distribution Model is used for estimating the number of faults initially resident in a program at the beginning of the test or debugging process based on the hypergeometric distribution. Let
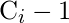
be the cumulative number of errors already detected so far by

, and let
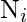
be the number of newly detected errors by time
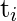
.
Assumptions:
- A program initially contains m faults when the test phase starts.
- A test is defined as a number of test instances which are couples of input data and output data. In other words, the collection of test operations performed in a day or a week is called a test instance. The test instances are denoted by
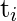 for i = 1, 2, . . ., n.
for i = 1, 2, . . ., n.
- Detected faults are not removed between test instances.
Therefore, from the latter assumption, the same faults can be experienced at several test instances. Let
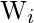
be the number of faults experienced by test instance
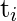
. It should be noted that some of the
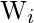
faults may be those that are already counted in
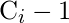
, and the remaining Wi faults account for the newly detected faults.
If
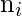
is an observed instance of
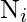
, then we can see that

. Each fault can be classified into one of two categories:
- Newly discovered faults
- Rediscovered faults
If we assume that the number of newly detected faults
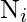
follows a hypergeometric distribution, then the probability of obtaining exactly
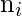
newly detected faults among
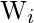
faults is,
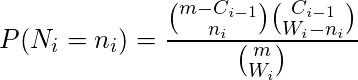
where
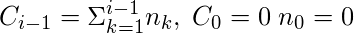
and
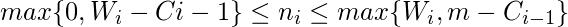
for all i. Since
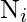
is assumed to be hypergeometrically distributed, the expected number of newly detected faults during the interval
![Rendered by QuickLaTeX.com $[t_{i-1}, t_i]$](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-94583e4a685b47c274103e6447506da7_l3.png)
is,
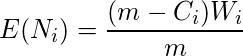
and the expected value of

is given by,
![Rendered by QuickLaTeX.com $$E(C_i)=m\left [1- \prod_{j=1}^i (1-p_i) \right ]$$](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-114fe799934bac78c7c7eb945a095280_l3.png)
where
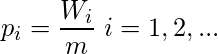
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...