Forms of Two-Variable Linear Equations – Straight Lines | Class 11 Maths
Last Updated :
01 Dec, 2020
Line is the simplest geometrical shape. It has no endpoints and extends in both directions till infinity. The word “straight” simply means without “bend”. The gradient between any two point on the line is same. Hence, we can say that, if the gradient between any two points on the line is same, then the locus is a straight line. So let’s see what are the different ways in the line can be represented.
Different Forms Of a Line
- Point Slope Form
- Two – Point Form
- Slope – Intercept Form
- Intercept Form
- Normal Form
Point – Slope Form
The equation of the line passing through the point (x1,y1) and slope ‘m’ can be written as :
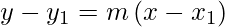
Proof:
Let the point that lies on the curve be (x1, y1) and any general point can be denoted by (h, k).
So, the slope of the line can be written as
Slope=(k-y1) / (h-x1)
Also, we know that the slope of line is m.
Hence,
(k-y1) / (h-x1)= m
Replace k by y and h by x
And, we get y – y1 = m(x – x1 )
Example 1.Write the equation of the line passing through (5,6) and slope equal to 3
Solution:
Putting the value of (x1,y1) as (5,6) and m = 3, we get
y – 6 = 3* (x -5)
y – 6 = 3x – 15
y = 3x – 9
Example 2.Write the equation of the line passing through (0,0) and slope equal to 1
Solution:
Putting the value of (x1,y1) as (0,0) and m=1, we get
y – 0 = 1* (x -0)
y = x
Two – Point Form
The equation of the line passing through the point (x1,y1) and (x2,y2) can be written as :
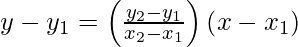
Proof:
Since we know any two points on the line, we can write the slope of the line as
m = (y2-y1) / (x2-x1)
And we also know from point slope form that
y-y1 = m(x-x1)
Substituting the value of m in the above equation, we get
y-y1 = ((y2-y1) / (x2-x1) * (x-x1)
Example 1.Write the equation of the line passing through (5,6) and (6,7)
Solution:
Putting the value of (x1,y1) as (5,6) and (x2,y2) as (6,7) , we get
y – 6 = (7-6)/(6-5) * (x -5)
y – 6 = 1* (x – 5)
y = x + 1
Example 2.Write the equation of the line passing through (0,5) and (5,5)
Solution:
Putting the value of (x1,y1) as (0,5) and (x2,y2) as (5,5), we get
y – 5 = (5-5)/(5-0) * (x -0)
y = 0
Slope – Intercept Form
The equation of line with slope ‘m’ and cutting a intercept ‘c’ on y-axis can be written as:
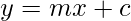
Proof:
Since y-intercept=c
Equation of line passing through (0,c) is given by
y – c = m(x-0)
y = mx + c
Example 1.Write the equation of the line having slope =5 and y-intercept as 3
Solution:
Putting the value of m=5 and c=3 in Equation y = mx + c
y = 5x+3
Example 2.Write the equation of the line having slope =1 and y-intercept as 1
Solution:
Putting the value of m=1 and c=1 in Equation y = mx + c
y = x+1
Intercept Form
The equation of the line cutting intercept ‘a’ on x-axis and ‘b’ on y-axis can be written as:
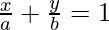
Proof:
So we know that the line passes through the point (a,0) and (0,b), we can write the equation using two point form
y – y1 = (y2 – y1) / (x2 – x1) * (x – x1)
Putting x1 = a, y1 = 0, x2 = 0 , y2 = b
We get,
y = (b/(-a) * (x-a)
Dividing both sides by b and simplify RHS we get
y/b = -(x/a)+1
⇒ x/a + y/b =1
Example 1.Write the equation of the line having x-intercept as 5 and y-intercept as 3
Solution:
Putting the value of a=5 and b=3 in Equation x / a + y / b = 1
x/5 + y/3 =1
Example 2.Write the equation of the line having x-intercept as 1 and y-intercept as 1
Solution:
Putting the value of a=1 and b=1 in Equation x / a + y / b = 1
x/1 + y/1 =1
Normal Form
The equation of the straight line upon which the length of the perpendicular from the origin is ‘p’ and this perpendicular makes an angle ‘∝’ with positive direction of x-axis is :
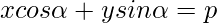
Proof:
Let the line AB be such that the length of the perpendicular OQ from the origin O to the line be p and <XOQ =∝.
From the diagram, using the intercept form we get
Equation of line AB is
x/p sec∝ + y/p cosec∝ =1
or
xcos∝ + ysin∝ =p
Example 1.Write the equation of the line for which the length of the perpendicular from the origin is 5 units and this perpendicular makes an angle of 450 with positive direction of x-axis.
Solution:
So, basically we are given the value of p=5 and ∝=450
Putting the values in the above equation we get,
x /√2 + y√2 = 5
x + y = 5√2
Example 2.Write the equation of the line for which the length of the perpendicular from the origin is 1 units and this perpendicular makes an angle of 600 With positive direction of x-axis.
Solution:
So, basically we are given the value of p=1 and ∝=600
Putting the values in the above equation we get,
x * (1/2) + y * (√3/2) = 1
x + y√3 = 2

Share your thoughts in the comments
Please Login to comment...