NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables

NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables is created by a team of professionals in the field of academic content, to help students resolve their doubts in solving problems given in the NCERT textbook. Use the expert-crafted Class 9 Mathematics Chapter 4 Linear Equations in Two Variables NCERT Answers to gain insights into the context and effective problem-solving approaches for this chapter. Find accurate solutions to all the exercise questions effortlessly. All of the problems in this chapter’s exercise from the NCERT textbook are covered in the NCERT Solutions for Class 9 Maths.

This chapter Linear Equations in Two Variables covers the introduction to linear equations, graphical representation of linear equations, techniques to solve them, formulating equations from real-life situations, and solving word problems. Students learn how to manipulate and solve linear equations in one variable using techniques such as simplification, isolation of the variable, and applying inverse operations.

Exercises under NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables

Class 9 Maths NCERT Solutions Chapter 4 Exercises:
NCERT Maths Solutions Class 9 Exercise 4.1 – 2 Questions & Solutions (2 Short Answers)
NCERT Maths Solutions Class 9 Exercise 4.2 – 4 Questions & Solutions (3 Short Answers, 1 Long Answer)
NCERT Maths Solutions Class 9 Exercise 4.3 – 8 Questions & Solutions (4 Short Answers, 4 Long Answers)
NCERT Maths Solutions Class 9 Exercise 4.4 – 2 Questions & Solutions (2 Long Answers)

NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables: Exercise 4.1

Question 1. The cost of a notebook is twice the cost of a pen. Write a linear equation in two variables to represent this statement.

Solution:

Let’s take the cost of a notebook as Rs. x and the cost of a pen as Rs. y.

Given that cost of a notebook (x) is twice the cost of a pen(y). 

So, x = 2y.

x – 2y = 0

x – 2y = 0 is the linear equation in two variables that represent the statement.

Question 2. Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case: 

(i) 2x + 3y = 9.35 

Solution:

2x + 3y – 9.35 = 0 (Transposing 9.35 to LHS)

(2)x + (3)y + (-9.35) = 0 (converting it in the form ax + by + c = 0)

On comparing equation with ax + by + c = 0, 

We get a = 2, b = 3, c = -9.35

(ii) x – y/5 -10 = 0

Solution:

(5x – y – 50)/5 = 0 (Multiply and divide the whole equation by 5)

5x – y – 50 = 0

(5)x + (-1)y + (-50) = 0 (converting it in the form ax + by + c = 0)

On comparing equation with ax + by +c =0, 

We get a = 5, b = -1, c = -50

(iii) -2x + 3y = 6

Solution:

-2x + 3y – 6 = 0 (Transposing 6 to LHS)

(-2)x + (3)y+ (-6) = 0 (converting it in the form ax + by + c = 0)

On comparing equation with ax + by +c =0, 

We get a = -2, b = 3, c = -6

(iv) x = 3y

Solution:

x – 3y = 0 (Transposing 3y to LHS)

(1)x + (-3)y + 0 = 0 (converting it in the form ax + by + c = 0)

On comparing equation with ax + by + c = 0, 

We get a = 1, b = -3, c = 0

(v) 2x = -5y

Solution:

2x + 5y = 0 (Transposing 5y to LHS)

(2)x + (5)y + 0 = 0 (converting it in the form ax + by + c = 0)

On comparing equation with ax + by +c =0, 

We get a = 2, b = 5, c = 0

(vi) x + 2 = 0

Solution:

(1)x + (0)y + 2 = 0 (converting it in the form ax + by + c = 0)

On comparing equation with ax + by +c =0, 

We get a = 1, b = 0, c = 2

(vii) y – 2 = 0

Solution:

(0)x + (1)y + (-2) = 0 (converting it in the form ax + by + c = 0)

On comparing equation with ax + by +c =0, 

We get a = 0, b = 1, c = -2 

(viii) 5 = 2x

Solution:

5 – 2x = 0 (Transposing 2x to LHS)

(-2)x + (0)y + 5 = 0 (converting it in the form ax + by + c = 0)

On comparing equation with ax + by + c = 0, 

We get a = -2, b = 0, c = 5

Linear Equations in Two Variables: Exercise 4.2

Question 1: Which one of the following options is true, and why?

y = 3x + 5 has

(i) a unique solution, (ii) only two solutions, (iii) infinitely many solutions

Solution:

Given linear equation: y = 3x + 5

Let x = 0, Therefore y = 3 × 0 + 5 

= 0 + 5 = 5

Hence, (0, 5) is one solution

Now, let x = 1, Therefore y = 3 × 1 + 5

= 3 + 5 = 7

Hence, (1, 8) is another solution

Now, let y = 0, Therefore 0 = 3x + 5

x = 5/3

Hence, (5/3, 0) is one another solution.

This concludes that different values of x and y give the different values of y and x respectively.

As there is also no end to the different types of solution for the linear equation in two variables. Therefore, it can have infinitely many solutions.

Hence, option “(iii) infinitely many solutions” is the correct answer.

Question 2: Write four solutions for each of the following equations:

(i) 2x + y = 7 

(ii) πx + y = 9 

(iii) x = 4y

Solution:

(i) 2x + y = 7 

Given: 2x + y = 7 

To find the four solutions we have to substitute different values for x.

Let x = 0

Then,

2x+y = 7

(2 × 0) + y = 7

y = 7

Therefore, we get (x, y) = (0, 7)

Let x = 1

Then,

2x+y = 7

(2×1)+y = 7

2+y = 7

y = 7-2

y = 5

Therefore, we get (x, y) = (1, 5)

Let x = 2

Then,

2x + y = 7

(2×2) + y = 7

4 + y = 7

y = 7 – 4

y = 3

Therefore, we get (x, y) = (2, 3)

Let x = 3

Then,

2x + y = 7

(2×3) + y = 7

6 + y = 7

y = 7 – 6

y = 1

Therefore, we get (x, y) = (3, 1)

Finally, the four solutions are (0, 7), (1,5), (2,3), (3, 1)

(ii) πx + y = 9

Given: πx+y = 9

To find the four solutions we have to substitute different values for x.

Let x = 0

Then,

πx + y = 9

(π×0) + y = 9

y = 9

Therefore, we get (x, y) = (0, 9)

Let x = 1

Then,

πx +y = 9

(π×1) + y = 9

π + y = 9

y = 9 – π

Therefore, we get (x, y) = (1, 9 – π)

Let x = 2

Then,

πx +y = 9

(π×2) + y = 9

2π + y = 9

y = 9 – 2π

Therefore, we get (x, y) = (1, 9 – 2π)

Let x = 3

Then,

πx +y = 9

(π×3) + y = 9

3π + y = 9

y = 9 – 3π

Therefore, we get (x, y) = (1, 9 – 3π)

Finally, the four solutions are (0, 9), (1, 9 – π), (2, 9 – 2π), (3, 9 – 3π)

(iii) x = 4y

Given: x = 4y

To find the four solutions we have to substitute different values for x.

Let x = 0

Then,

x = 4y

0 = 4y

4y= 0

y = 0/4

y = 0

Therefore, we get (x, y) = (0,0)

Let x = 1

Then,

x = 4y

1 = 4y

4y = 1

y = 1/4

Therefore, we get (x, y) = (1,1/4)

Let x = 2

Then,

x = 4y

2 = 4y

4y = 2

y = 2/4

Therefore, we get (x, y) = (2, 1/2)

Let x = 3

Then,

x = 4y

3 = 4y

4y = 3

y = 3/4

Therefore, we get (x, y) = (2, 3/4)

Finally, the four solutions are (0, 0), (1,1/4), (2, 1/2), (2, 3/4)

Question 3: Check which of the following are solutions of the equation x – 2y = 4 and which are not:

(i) (0, 2) 

(ii) (2, 0) 

(iii) (4, 0)

(iv) (√2 , 4√2) 

(v) (1, 1)

Solution:

(i) (0, 2)

Given: x – 2y = 4

As, x=0 and y=2

Hence, substituting the values of x and y in the equation, we get,

x – 2y = 4

0 – (2×2) = 4

-4 ≠ 4

L.H.S ≠ R.H.S

Therefore, (0, 2) is not a solution to the given equation x – 2y = 4.

(ii) (2, 0)

Given: x – 2y = 4

As, x = 2 and y = 0

Hence, substituting the values of x and y in the equation, we get,

x – 2y = 4

2 – (2×0) = 4

2 – 0 = 4

2 ≠ 4

L.H.S ≠ R.H.S

Therefore, (2, 0) is not a solution to the given equation x – 2y = 4.

(iii) (4, 0)

Given: x – 2y = 4

As, x= 4 and y=0

Hence, substituting the values of x and y in the equation, we get,

x – 2y = 4

4 – 2×0 = 4

4 – 0 = 4

4 = 4

L.H.S = R.H.S

Therefore, (4, 0) is a solution to the given equation x – 2y = 4.

(iv) (√2, 4√2)

Given: x – 2y = 4

As, x = √2 and y = 4√2

Hence, substituting the values of x and y in the equation, we get,

x – 2y = 4

√2 – (2×4√2) = 4

√2 – 8√2 = 4

-7√2 ≠ 4

L.H.S ≠ R.H.S

Therefore, (√2, 4√2) is not a solution to the given equation x – 2y = 4.

(v) (1, 1)

Given: x – 2y = 4

As, x= 1 and y= 1

Hence, substituting the values of x and y in the equation, we get,

x – 2y = 4

1 – (2×1) = 4

1 – 2 = 4

-1 ≠ 4

L.H.S ≠ R.H.S

Therefore, (1, 1) is not a solution to the given equation x – 2y = 4.

Question 4: Find the value of k, if x = 2, y = 1 is a solution of the equation 2x + 3y = k.

Solution:

Given: 2x + 3y = k

According to the question, x = 2 and y = 1 is solution of the given equation.

Hence, substituting the values of x and y in the equation 2x+3y = k, we get,

2x + 3y = k

(2×2) + (3×1) = k

4 + 3 = k

7 = k

k = 7

Therefore, the value of k is 7.

Linear Equations in Two Variables: Exercise 4.3

Question 1. Draw the graph of each of the following linear equations in two variables:

(i) x + y = 4 

(ii) x – y = 2 

(iii) y = 3x 

(iv) 3 = 2x + y

Solution:

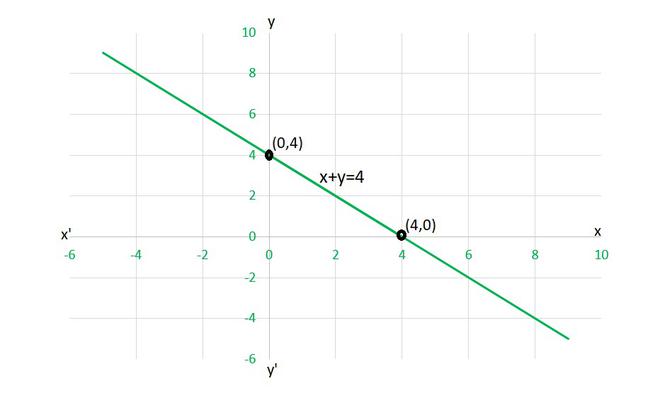
(i) To draw the graph x+y=4, we need at least two solutions of the equation. 

We can check that when, x = 0, y = 4, 

and x = 4, y = 0 

are solutions of the given equation. So, we can use the following table to draw the graph:

x	y
0	4
4	0

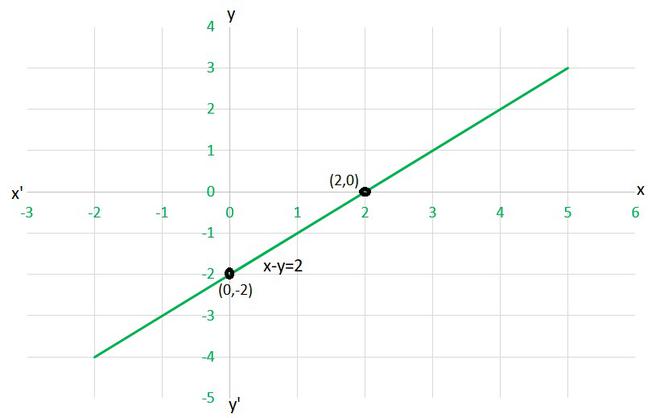
(ii) To draw the graph x-y=2, we need at least two solutions of the equation.

We can check that when, x = 0, y = -2,

and x = 2, y = 0

are solutions of the given equation. So, we can use the following table to draw the graph:

x	y
0	-2
2	0

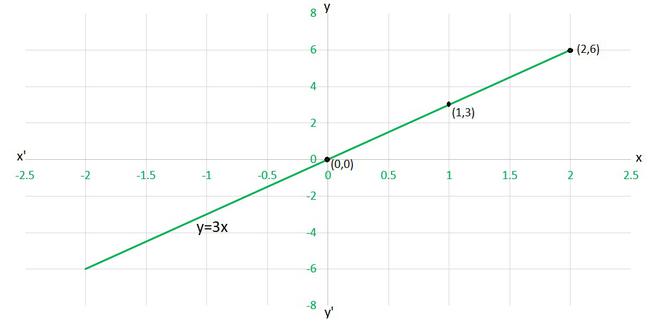
(iii) To draw the graph y=3x, we need at least two solutions of the equation.

We can check that when, x = 0, y =0,

and x = 1, y = 3

are solutions of the given equation. So, we can use the following table to draw the graph :

x	y
0	0
1	3

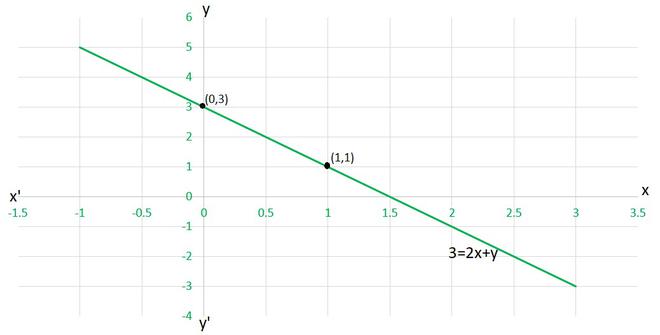
(iv) To draw the graph 3=2x+y, we need at least two solutions of the equation.

We can check that when, x = 0, y =3,

and x = 1, y = 1

are solutions of the given equation. So, we can use the following table to draw the graph :

x	y
0	3
1	1

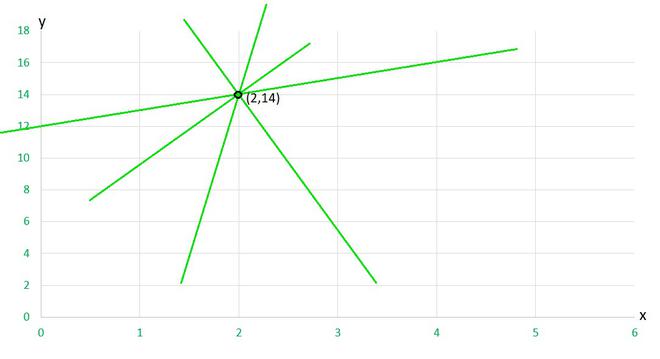
Question 2. Give the equations of two lines passing through (2, 14). How many more such lines are there, and why?

Solution:

Here, as given point is (2,14) so

x=2 and y=14

We can form various equation such as,

y-x = 14-2 = 12

x+y = 2+14 =16

2x+y = 4+14 = 18

y-2x = 14-4 = 10

y = 14

x = 2

and many more……..

In fact, there are infinitely many linear equations which are satisfied by the coordinates of the point (2, 14).

As it is stated that there can be infinite lines passing through a point. So here,

⟹

Question 3. If the point (3, 4) lies on the graph of the equation 3y = ax + 7, find the value of a.

Solution:

The given equation is

3y = ax+7

According to the given point (3,4), 

x = 3 and y = 4

As this point lie on this graph, then it will satisfy these points. So substituting the values 

3y = ax+7

⟹ (3×4) = (a×3)+7

12 = 3a+7

 3a = 12–7

3a = 5

a = [Tex]\frac{5}{3} [/Tex]

Hence, the value of a = [Tex]\frac{5}{3}  [/Tex].

Question 4. The taxi fare in a city is as follows: For the first kilometer, the fare is ₹ 8 and for the subsequent distance it is ₹ 5 per km. Taking the distance covered as x km and total fare as ₹ y, write a linear equation for this information, and draw its graph.

Solution:

So, as given in the question, we will take 

Distance covered as x km 

and total fare as ₹ y

Fare for the first kilometer = 8 per km

Fare after the first 1km = ₹ 5 per km

Let x is the total distance, then the distance after one km will be = (x-1)km

Hence., Fare after the first km = 5(x-1)

So, in equation form we can conclude that, 

The total fare = Fare of first km+ fare after the first km

y = 8+5(x-1)

y = 8+5(x-1)

y = 8+5x – 5

y = 5x+3

To draw the graph y=5x+3, we need at least two solutions of the equation.

We can check that when, x = 0, y =3,

and x = -1, y = -2

are solutions of the given equation. So, we can use the following table to draw the graph :

x	y
0	3
-1	-2

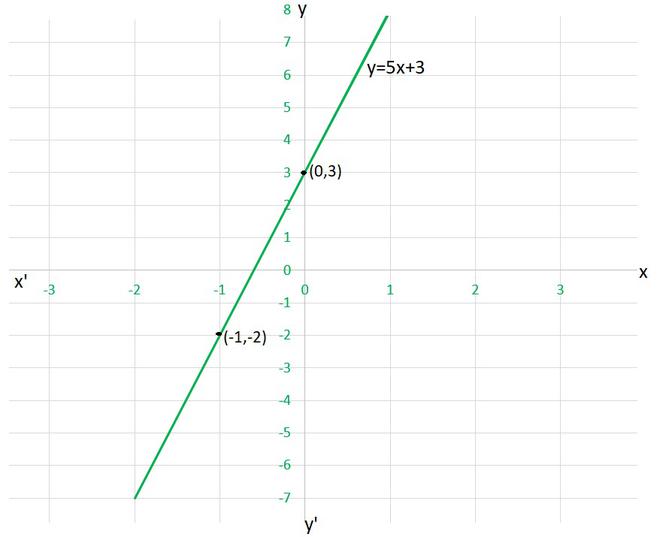
Question 5. From the choices given below, choose the equation whose graphs are given in Fig. 4.6 and Fig. 4.7.

For Fig. 4. 6 

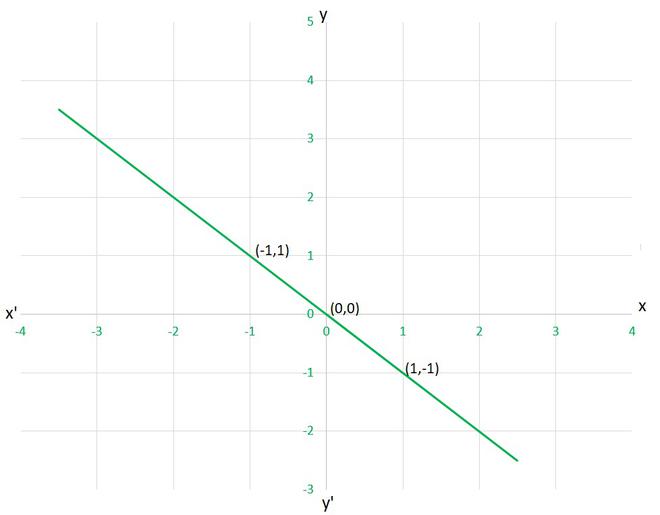
(i) y = x 

(ii) x + y = 0 

(iii) y = 2x 

(iv) 2 + 3y = 7x 

Solution:

Let’s check each given cases, whether they are satisfying the solution given on graph or not,

(i) y=x

as given point  (1,-1)

x=1 and y=-1 ⟹ x≠y

Hence, this equation is INCORRECT for this graph.

(ii) x+y=0

as given point (1,-1), (1,-1) and (0,0)

x=1 and y=-1 ⟹ x+y=0

x=-1 and y=1 ⟹ x+y=0

x=0 and y=0 ⟹ x+y=0

Hence, this equation is CORRECT for this graph.

(iii) y=2x

as given point  (1,-1)

x=1 and y=-1 ⟹ y≠2x

Hence, this equation is INCORRECT for this graph.

(iii) 2+3y=7x

as given point  (1,-1)

x=1 and y=-1 ⟹ 2+3y≠7x

Hence, this equation is INCORRECT for this graph.

For Fig. 4.7

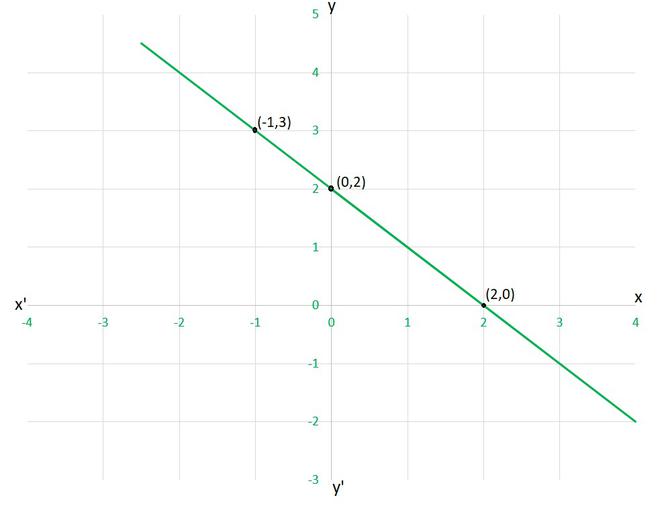
(i) y = x + 2

(ii) y = x – 2

(iii) y = –x + 2

(iv) x + 2y = 6

Solution:

Let’s check each given cases, whether they are satisfying the solution given on graph or not,

(i) y=x+2

as given point (0,2), (2,0) and (-1,3)

x=0 and y=2 ⟹ y=x+2

x=2 and y=0 ⟹ y≠x+2

Hence, this equation is INCORRECT for this graph.

(ii) y=x-2

as given point (0,2)

x=0 and y=2 ⟹ y≠x-2

Hence, this equation is INCORRECT for this graph.

(iii) y=-x+2

as given point (0,2)

x=0 and y=2 ⟹ y=-x+2

x=2 and y=0 ⟹ y=-x+2

x=-1 and y=3 ⟹ y=-x+2

Hence, this equation is CORRECT for this graph.

(iii) x+2y=6

as given point (0,2)

x=0 and y=2 ⟹ x+2y≠6

Hence, this equation is INCORRECT for this graph.

Question 6. If the work done by a body on application of a constant force is directly proportional to the distance travelled by the body, express this in the form of an equation in two variables and draw the graph of the same by taking the constant force as 5 units. Also read from the graph the work done when the distance travelled by the body is 

(i) 2 units 

(ii) 0 unit

Solution:

Given in question,

Work done = force × displacement

where constant force = 5 units

lets take work done as y units

and, distance travelled by the body x units

Hence, the equation can be expressed as,

y=5x

To draw the graph y=5x, we need at least two solutions of the equation.

We can check that when, x = 0, y =0,

and x = 1, y = 5

are solutions of the given equation. So, we can use the following table to draw the graph :

x	y
0	0
1	5

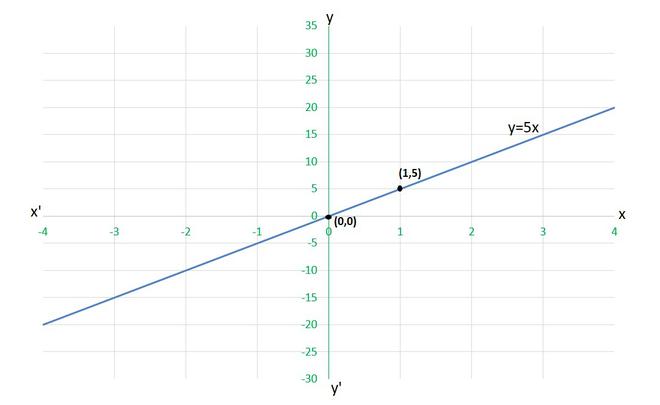
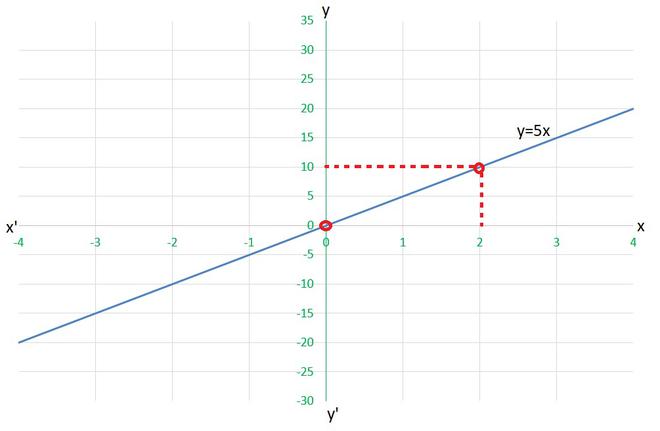
(i) for x= 2 units

y=5×2

work done = 10 units

(ii) for x= 0 units

y=5×0

work done = 0 units

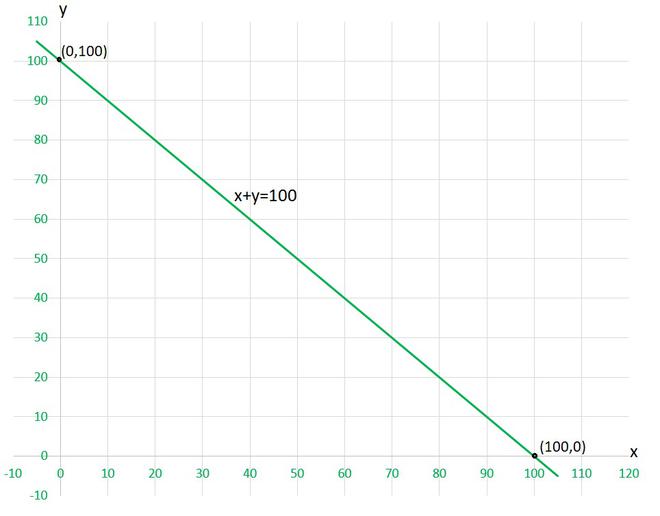
Question 7. Yamini and Fatima, two students of Class IX of a school, together contributed ₹ 100 towards the Prime Minister’s Relief Fund to help the earthquake victims. Write a linear equation that satisfies this data. (You may take their contributions as ₹ x and ₹ y). Draw the graph of the same. 

Solution:

Let’s take Yamini’s contribution as ₹ x and Fatima’s contribution as ₹ y.

As they together contributed ₹ 100, so the equation can be formed as,

x+y=100

To draw the graph x+y=100, we need at least two solutions of the equation.

We can check that when, x = 0, y =100,

and x = 100, y = 0

are solutions of the given equation. So, we can use the following table to draw the graph :

x	y
0	100
100	0

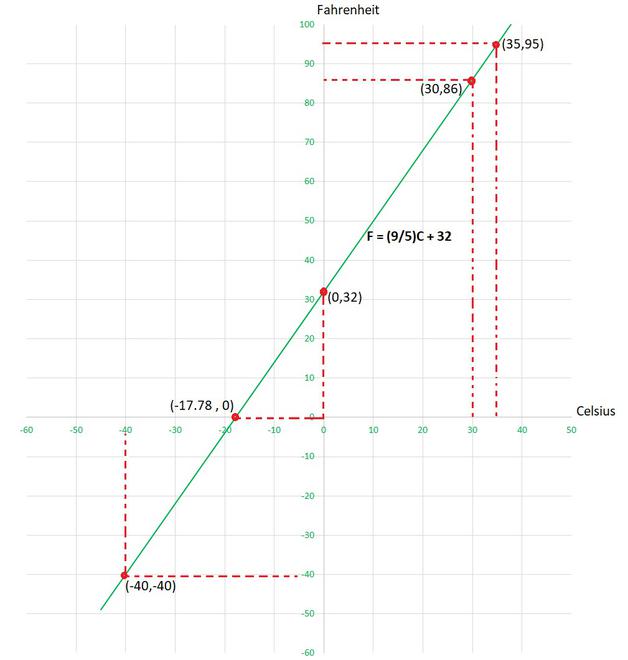
Question 8. In countries like USA and Canada, temperature is measured in Fahrenheit, whereas in countries like India, it is measured in Celsius. Here is a linear equation that converts Fahrenheit to Celsius:

F = [Tex]\mathbf{\frac{9}{5}}   [/Tex]C + 32

(i) Draw the graph of the linear equation above using Celsius for x-axis and Fahrenheit for y-axis.

(ii) If the temperature is 30°C, what is the temperature in Fahrenheit?

(iii) If the temperature is 95°F, what is the temperature in Celsius?

(iv) If the temperature is 0°C, what is the temperature in Fahrenheit and if the temperature is 0°F, what is the temperature in Celsius?

(v) Is there a temperature which is numerically the same in both Fahrenheit and Celsius? If yes, find it.

Solution:

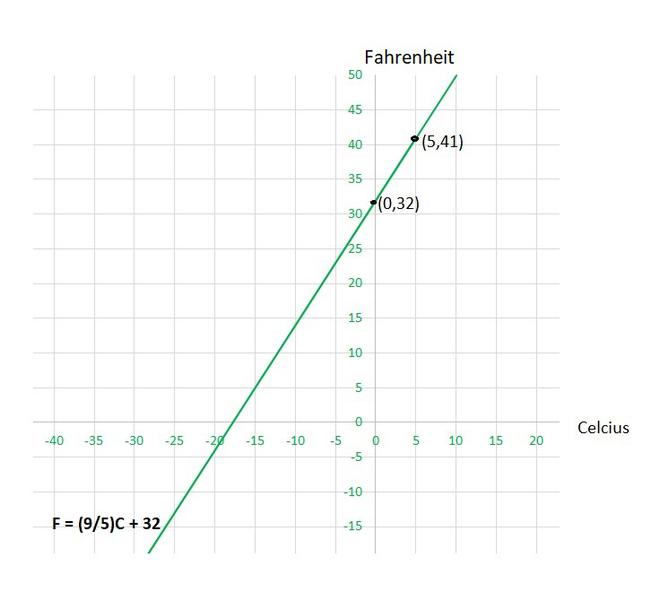
(i) Taking Celsius on x-axis and Fahrenheit on y-axis , so equation will be as follows:

y = [Tex]\frac{9}{5}   [/Tex]x + 32

To draw the graph y = [Tex]\frac{9}{5}  [/Tex]x + 32, we need at least two solutions of the equation.

We can check that when, x = 0, y =32,

and x = 5, y = 41

are solutions of the given equation. So, we can use the following table to draw the graph :

x	y
0	32
5	41

(ii) When the temperature is 30°C then, using the equation

y = [Tex]\frac{9}{5}   [/Tex]x + 32

by substituting, x=30, we get

y = [Tex]\frac{9}{5}   [/Tex]×30 + 32

y = 86 

Hence, in Fahrenheit temperature will be 86°F

(iii) When the temperature is 95°F then, using the equation

y = [Tex]\frac{9}{5}   [/Tex]x + 32

by substituting, y=95, we get

95 = [Tex]\frac{9}{5}   [/Tex]x+ 32

x = [Tex]\frac{(95-32)×5}{9} [/Tex]

x = 35

Hence, in Celsius temperature will be 35°C

(iv)When the temperature is 0°C, using the equation

y = [Tex]\frac{9}{5}   [/Tex]x + 32

by substituting, x=0, we get

y = [Tex]\frac{9}{5}   [/Tex]×0 + 32

y = 32

Hence, in Fahrenheit temperature will be 32°F

and, when the temperature is 0°F, using the equation and by substituting, y=0, we get

0 = [Tex]\frac{9}{5}   [/Tex]x + 32

x = [Tex]\frac{(-32)×5}{9} [/Tex]

x = -17.78

Hence, in Celsius temperature will be -17.78°C.

(v) Lets take both temperature same as x.

so, equation becomes as follows:

x = [Tex]\frac{9}{5}   [/Tex]x + 32

[Tex]\frac{9}{5}   [/Tex]x-x = -32

[Tex]\frac{4}{5}   [/Tex]x = -32

x = -32×[Tex]\frac{4}{5} [/Tex]

x = -40

Hence, Celsius and Fahrenheit temperature will be -40°C and -40°F respectively.

Linear Equations in Two Variables: Exercise 4.4

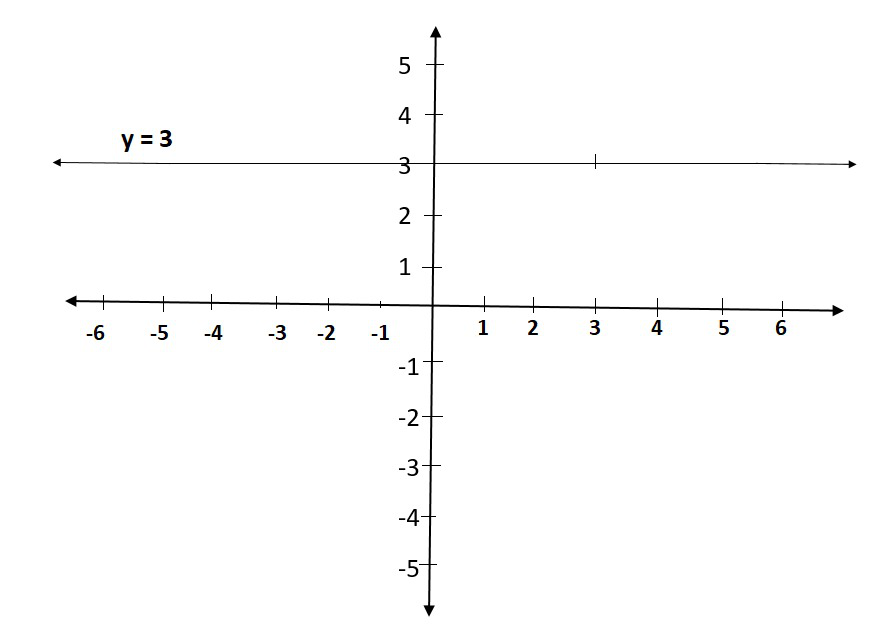
Question 1. Give the geometric representations of y = 3 as an equation

(i) in one variable

(ii) in two variables

Solution:

(i) If y = 3 is treated as a equation in one variable y only, then it has the unique solution

y = 3, which is a point on the number line

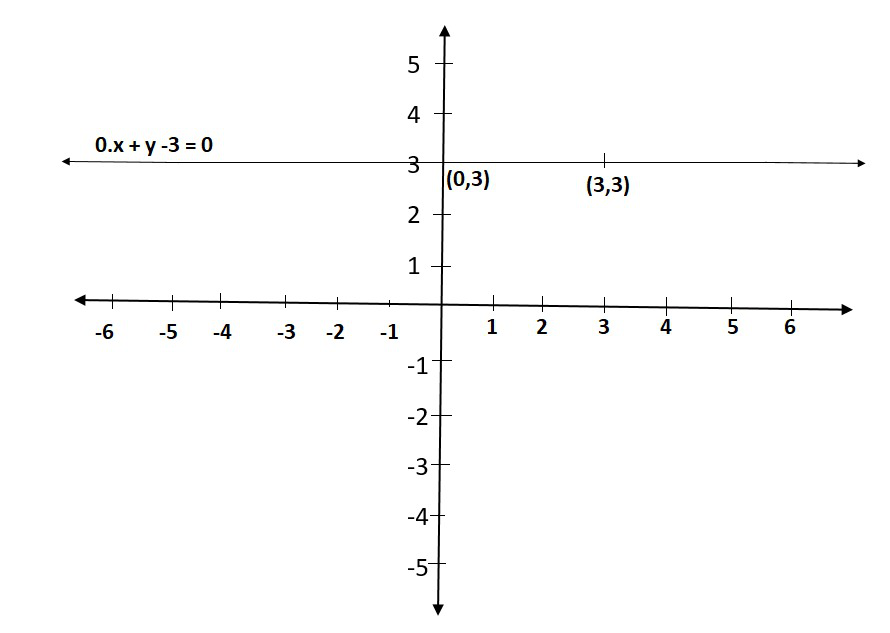
(ii) When an equation in two variables, it can be expressed as,

0.x + y – 3 = 0

which is a linear equation in the variables x and y. This is represented by a line. Now all the values of x are permissible because 0.x is always 0. However, y must satisfy the equation y = 3

This has infinitely many solutions. In fact, they are all of the form (r, 3), where r is any real number, so

We can have these two solutions for making line on a graph as:

x	y
0	3
3	3

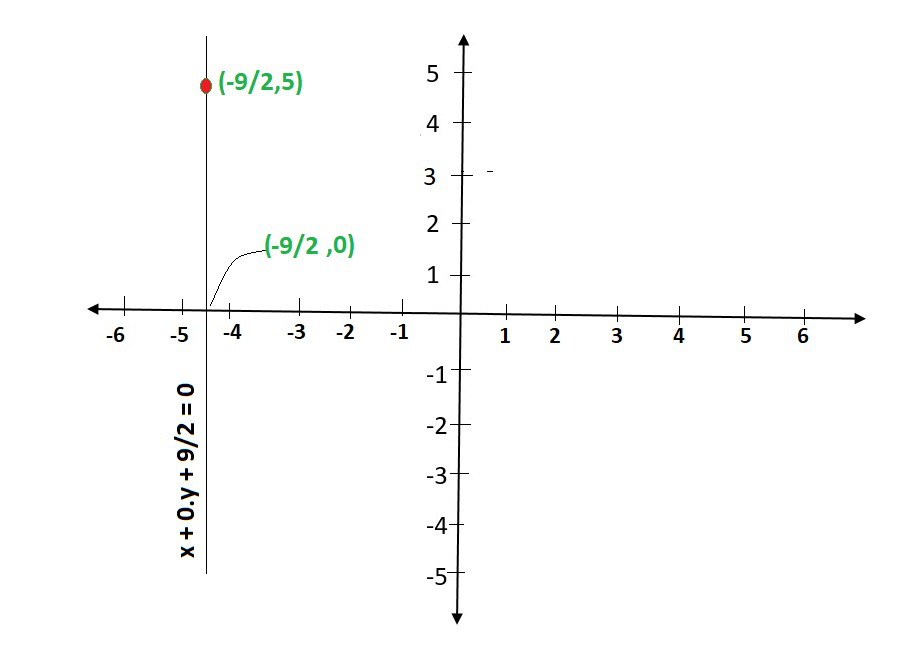
Question 2. Give the geometric representations of 2x + 9 = 0 as an equation

(i) in one variable

(ii) in two variables

Solution:

Firstly, we solve 2x + 9 = 0, to get

x = -9/2

(i) If x = -9/2 is treated as a equation in one variable x only, then it has the unique solution

x = -9/2, which is a point on the number line.

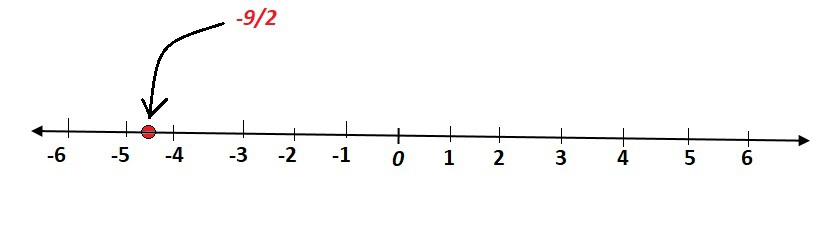
(ii) When an equation in two variables, it can be expressed as,

x + 0.y + 9/2 = 0

which is a linear equation in the variables x and y. This is represented by a line. Now all the values of y are permissible because 0.y is always 0. However, x must satisfy the equation x = -9/2

This has infinitely many solutions. In fact, they are all of the form (-9/2, r), where r is any real number, so

We can have these two solutions for making line on a graph as:

x	y
-9/2	0
-9/2	5

Types Of Questions In NCERT Class 9 Chapter 4

NCERT Grade 9 CBSE Chapter 4 Linear Equations in Two Variables, falls under the Algebra section. It introduces the concept of solving linear equations with two variables and their graphical representation on a Cartesian plane. The chapter covers essential considerations for solving linear problems and provides solutions for linear equations with two variables. Guided examples make learning more engaging, and exercises help assess understanding. Topics include graphing linear equations, lines parallel to the x-axis and y-axis, and solutions are presented step by step for gradual comprehension.

Benefits of Class 9 Maths Chapter 4 Linear Equations in Two Variables NCERT Solutions

Access all exercise question answers in one convenient location. Gain insights into expertly solved solutions, available for download or online access, to enhance your effectiveness in tackling exercises. Utilize these solutions to hone your problem-solving abilities and grasp the mathematical principles applicable to linear equations with two variables.

Independently resolve doubts associated with exercise questions, ensuring no query goes unanswered and elevating your preparation. Learn from experts’ unique problem-solving approaches for specific questions and apply these insights confidently.

FAQs – NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations In Two Variables

1. What can I learn from Maths Class 9 Chapter 4?

This chapter extends the understanding of linear equations from one variable to two variables. Any equation that can be expressed in the form ax + by + c = 0, where a, b, and c are real numbers, and both ‘a’ and ‘b’ are not zero, is defined as a linear equation in two variables. The NCERT solutions for Class 9 Maths offer chapter-wise answers to exercises in the textbook, allowing students to grasp the concept of linear equations in Algebra through straightforward examples.

2. What are all the important topics that need to be covered to score in Class 9 Maths Chapter 4?

Key topics essential for a thorough understanding of Class 9 Maths Chapter 4, ‘Linear Equations in Two Variables,’ include expressing linear equations in the form Ax + By + C = 0, exploring various solutions of linear equations with two variables, graphing linear equations in two variables, and understanding equations of lines parallel to the x-axis and y-axis. To gain clarity on these concepts, it’s crucial to solve all examples and exercise questions.

3. Is Chapter 4 of Linear Equation in Two Variables of Class 9 Maths tough?

No, the NCERT Class 9 Mathematics Chapter 4 Linear Equations in Two Variables, isn’t challenging for those who diligently practice the chapter. The key is to complete the chapter comprehensively, including all examples, exercise questions, and additional problems. To navigate Class 9 Maths Chapter 4 with ease, NCERT Solutions Class 9 Maths Chapter 4 on Linear Equations in Two Variables by GeeksforGeeks is your ideal resource.