Class 11 NCERT Solutions – Chapter 8 Binomial Theorem – Exercise 8.2
Last Updated :
01 Apr, 2021
Question 1. Find the coefficient of x5 in (x+3)8
Solution:
The (r+1)th term of (x+3)8 is given by Tr+1 = 8Cr(x)8-r(3)r (eq1).
Therefore for x5 we need to get 8-r =5 (Because we need to find x5. Therefore, power ox must be equal to 5)
So we get r=3.
Now, put r=3 in eq1. We get,
Coefficient of x5 = 8C3(x)5(3)3 = 8!*33/(4!*4!) = 1512
Coefficient of x5 is 1512.
Question 2. Find the coefficient of a5b7 in (a-2b)12.
Solution:
The (r+1)th term of (a-2b)12 is given by Tr+1 = 12Cr(a)12-r(-2b)r × (eq1)
In the question it is given that exponent of b is 7. Therefore, r should be equal to 7.
By putting r=7 in eq1, we get
Coefficient of a5b7 = 12C7(-2)7 = -101376
Question 3. Write the general term in the expansion of (x2−y)6.
Solution:
General term of the equation (a+b)n is given as Tr+1 = nCr(a)n-r(b)r.
In this question a= x2 and b=-y. After putting the value of a, b and n, we get the general term as
Tr+1 = 6Cr(x2)(12-r)(-y)6 = (-1)r 6Cr(x)(12-2r)(y)r.
Question 4. Write the general term in the expansion of (x2-yx)12.
Solution:
General term of the equation (a+b)n is given as Tr+1 = nCr(a)n-r(b)r.
In this question a= x2 and b=-yx. After putting the value of a, b and n, we get the general term as
Tr+1 = 12Cr(x2)(12-r)(-yx)r = (-1)r 12Cr(x)(24-2r)(y)r(x)r = (-1)r 12Cr(x)(24-r)(y)r
Question 5. Find the 4th term in the expansion of (x-2y)12
Solution:
General term in the expansion of (a+b)n is written as Tr+1 = nCr(a)n-r(b)r
In the question we are given that a = x, b = -2y and n=12.
To get the 4th term, we need to put r = 3 (Because r+1=4, therefore r=3).
Therefore, T4 = 12C3(x)12-3(-2y)3 = −1760x9y3
Question 6. Find the 13th term in the expansion of (9x-1/3√x)18
Solution:
General term in the expansion of (a+b)n is written as Tr+1 = nCr(a)n-r(b)r
In this question a = 9x, b= -1/3√x and n=18.
To get the 13th term, we need to put r=12 (Because r+1=13, therefore r=12).
Therefore, T13 = 18C12(9x)18-12(-1/3√x)12 = 18564
Question 7. Find the middle terms in the expansion of (3−x3/6)7.
Solution:
In the expansion of (a+b)n, if n is odd, then there are two middle terms, namely, ((n+1)/2)th and ((n+1)/2+1)th term.
Therefore, middle terms in the expansion of (3−x3/6)7are 4th term and 5th term.
T4 = T3+1 = 7C3(3)7-3(−x3/6)3 = (-1)37!34x9/4!.3!63=-105x9/8
T5 = T4+1 = 7C4(3)7-4(−x3/6)4= (-1)47!33x12/4!3!64 = 35x12/48
Thus, the middle terms are -105x9/8 and 35x12/48.
Question 8. Find the middle terms in the expansion of (x/3+9y)10
Solution:
In the expansion of (a+b)n, if n is even, then the middle term is (n/2+1)th term.
Therefore, the middle term is 6th term.
T6 = T5+1 = 10C5(x/3)5(9y)5= (10!x595y5)/(5!5!35) = 61236x5y5
Thus, the middle term is 61236x5y5
Question 9. In the expansion of (1+a)m+n, prove that coefficients of am and an are equal.
Solution:
Let us assume that am occurs in the (r+1)th term, we obtain
Tr+1 = m+nCr(1)m+n-r(a)r = m+nCrar
Comparing the indices of a in am and in Tr+1, we obtain r=m
Therefore, the coefficient of am is m+nCm = (m+n)!/m!n! …(1)
Let us assume that an occurs in the (k+1)th, we obtain
Tk+1 = m+nCk(1)m+n-k(a)k = m+nCkak
Comparing the indices of a in an and Tk+1, we obtain k-n
Therefore, the coefficient of an is m+nCn = (m+n)!/m!n! ….(2)
Thus, from (1) and (2), it can be obtained that the coefficients of am and an are equal.
Question 10. The coefficients of the (r-1)th, rth and (r+1)th terms in the expansion of (x+1)n are in the ratio of 1:3:5. Find n and r.
Solution:
(r-1)th term in the expansion of (x+1)n is Tr-1 = nCr-2(x)n-(r-2)(1)r-2 = nCr-2(x)n-r+2
rth term in the expansion of (x+1)n is Tr = nCr-1(x)n-(r-1)(1)r-1 = nCr-1(x)n-r+1
(r+1)th term in the expansion of (x+1)n is Tr+1= nCr(x)n-r(1)r = nCr(x)n-r
Therefore the coefficients of (r-1)th , rth and (r+1)th in the expansion of (x+1)n are nCr-2, nCr-1 and nCr respectively.
Since these coefficients are in the ratio of 1:3:5, we obtain
nCr-2/nCr-1 = 1/3 and nCr-1/nCr = 3/5
Solving these two equations we get n-4r+5=0 and 3n-8r+3=0.
After solving these two equations, we get n=7 and r=3
Thus n=7 and r=3.
Question 11. Prove that the coefficient of x^n in the expansion of (1+x)2n is twice the coefficient of xn in the expansion of (1+x)2n-1.
Solution:
In the expansion of (1+x)2n, Tn+1 = 2nCn(1)2n-n(x)n = 2nCnxn
Therefore, coefficient of xn in the expansion of (1+x)2n is 2nCn
2nCn = (2n)!/(n!)2 ….(1)
Similarly, coefficient of xn in the expansion of (1+x)2n-1 is 2n-1Cn
2n-1Cn = (2n)!/2.(n!)2 …(2)
From (1) and (2), 2.2n-1Cn = 2nCn
Hence, it is proved that the coefficient of xn in the expansion of (1+x)2n is twice the coefficient of xn in the expansion of (1+x)2n-1
Question 12. Find a positive value of m for which the coefficient of x2 in the expansion of (1+x)m is 6.
Solution:
General term Tr+1 = mCr(1)m-r(x)r = mCr(x)r
Comparing the indices of x in x2 and Tr+1, we get r=2
Therefore, mC2 = 6
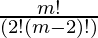 = 6
= 6
m!/(m-2)!=12
m(m-1) = 12=> m2-m-12 = 0
(m-4)(m+3) = 0
m cannot be negative. Therefore, m=4
Share your thoughts in the comments
Please Login to comment...