Class 11 NCERT Solutions- Chapter 8 Binomial Theorem – Exercise 8.1
Last Updated :
03 Mar, 2021
Theorem 1:
(a+b)n = 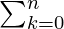 nCk an-k bk
nCk an-k bk
Here, the coefficients nCk are known as binomial coefficients.
Theorem 2:
(a–b)n = 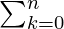 (-1)n nCk an-k bk
(-1)n nCk an-k bk
Expand each of the expressions in Exercises 1 to 5.
Question 1. (1 – 2x)5
Solution:
According to theorem 2, we have
a = 1
b = 2x
and, n = 5
So, (1 – 2x)5 = 5C0 (1)5 – 5C1 (1)4 (2x)1 + 5C2 (1)3 (2x)2 – 5C3 (1)2 (2x)3 + 5C4 (1)1 (2x)4 – 5C5 (2x)5
= 1 – 5 (2x) + 10 (4x)2 – 10 (8x3) + 5 (16 x4) – (32 x5)
= 1 – 10x + 40x2 – 80x3 + 80x4– 32x5
Question 2. 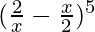
Solution:
According to theorem 2, we have
a = 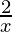
b = 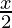
and, n = 5
So,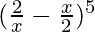 = 5C0 (
= 5C0 (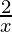 )5 – 5C1 (
)5 – 5C1 (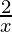 )4 (
)4 (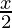 )1 + 5C2 (
)1 + 5C2 (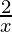 )3 (
)3 (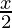 )2 – 5C3 (
)2 – 5C3 (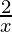 )2 (
)2 (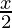 )3 + 5C4 (
)3 + 5C4 (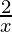 )1 (
)1 (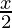 )4 – 5C5 (
)4 – 5C5 (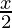 )5
)5
= 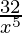 – 5
– 5 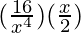 + 10
+ 10 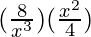 – 10
– 10 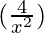 + 5
+ 5 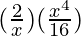 –
– 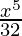
= 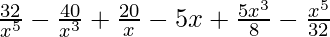
Question 3. (2x – 3)6
Solution:
According to theorem 2, we have
a = 2x
b = 3
and, n = 6
So, (2x – 3)6 = 6C0 (2x)6 – 6C1 (2x)5 (3)1 + 6C2 (2x)4 (3)2 – 6C3 (2x)3 (3)3 + 6C4 (2x)2 (3)4 – 6C5 (2x)1 (3)5 + 6C6 (3)6
= 64x6 – 6(32x5)(3) + 15 (16x4) (9) – 20 (8x3) (27) + 15 (4x2) (81) – 6 (2x) (243) + 729
= 64x6 – 576x5 + 2160x4 – 4320x3 + 4860x2 – 2916x + 729
Question 4. 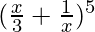
Solution:
According to theorem 1, we have
a = 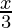
b = 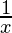
and, n = 5
So, 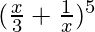 = 5C0 (
= 5C0 (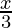 )5 + 5C1 (
)5 + 5C1 (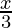 )4 (
)4 ( )1 + 5C2 (
)1 + 5C2 (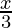 )3 (
)3 ( )2 + 5C3 (
)2 + 5C3 (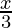 )2 (
)2 ( )3 + 5C4 (
)3 + 5C4 (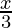 )1 (
)1 ( )4 + 5C5 (
)4 + 5C5 ( )5
)5
= 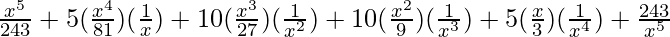
= 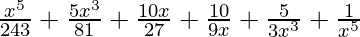
Question 5. 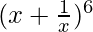
Solution:
According to theorem 1, we have
a = x
b = 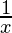
and, n = 6
So, 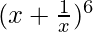 = 6C0 (x)6 + 6C1 (x)5 (
= 6C0 (x)6 + 6C1 (x)5 ( )1 + 6C2 (x)4 (
)1 + 6C2 (x)4 ( )2 + 6C3 (x)3 (
)2 + 6C3 (x)3 ( )3 + 6C4 (x)2 (
)3 + 6C4 (x)2 ( )4 + 6C5 (x)1 (
)4 + 6C5 (x)1 ( )5 + 6C6 (
)5 + 6C6 ( )6
)6
= 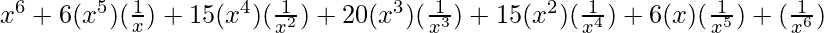
= 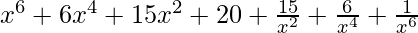
Using the binomial theorem, evaluate each of the following:
Question 6. (96)3
Solution:
Given: (96)3
Here, 96 can be expressed as (100 – 4).
So, (96)3 = (100 – 4)3
According to Theorem 2, we have
= 3C0 (100)3 – 3C1 (100)2 (4) – 3C2 (100) (4)2– 3C3 (4)3
= (100)3 – 3 (100)2 (4) + 3 (100) (4)2 – (4)3
= 1000000 – 120000 + 4800 – 64
= 884736
Question 7. (102)5
Solution:
Given: (102)5
Here, 102 can be expressed as (100 + 2).
So, here (102)5 = (100 + 2)5
According to Theorem 1, we have
= 5C0 (100)5 + 5C1 (100)4 (2) + 5C2 (100)3 (2)2 + 5C3 (100)2 (2)3 + 5C4 (100) (2)4 + 5C5 (2)5
= (100)5 + 5 (100)4 (2) + 10 (100)3 (2)2 + 10 (100) (2)3 + 5 (100) (2)4 + (2)5
= 10000000000 + 1000000000 + 40000000 + 80000 + 8000 + 32
= 11040808032
Question 8. (101)4
Solution:
Given: (101)4
Here, 101 can be expressed as (100 + 1).
So, here (101)4 = (100 + 1)4
According to Theorem 1, we have
= 4C0 (100)4 + 4C1 (100)3 (1) + 4C2 (100)2 (1)2 + 4C3 (100) (1)2 + 4C4 (1)4
= (100)4 + 4 (100)3 + 6 (100)2 + 4 (100) + (1)4
= 100000000 + 400000 + 60000 + 400 + 1
= 1040604001
Question 9. (99)5
Solution:
Given: (99)5
Here, 99 can be expressed as (100 – 1).
So, here (99)5 = (100 – 1)5
According to Theorem 2, we have
= 5C0 (100)5 – 5C1 (100)4 (1) + 5C2 (100)3 (1)2 – 5C3 (100)2 (1)3 + 5C4 (100) (1)4 – 5C5 (1)5
= (100)5 – 5 (100)4 + 10 (100)3 – 10 (100)2 + 5 (100) – 1
= 1000000000 – 5000000000 + 10000000 – 100000 + 500 – 1
= 9509900499
Question 10. Using Binomial Theorem, indicate which number is larger (1.1)10000 or 1000.
Solution:
Given: (1.1)10000
Here, 1.1 can be expressed as (1 + 0.1)
So, here (1.1)10000 = (1 + 0.1)10000
According to Theorem 1, we have
(1 + 0.1)10000 = 10000C0 (1)10000 + 10000C1 (1)9999 (0.1)1 + other positive terms
= 1 + 1000 + other positive terms
= 1100 + other positive terms
So, 1100 + other positive terms > 1000
Hence, proved (1.1)10000 > 1000
Question 11. Find (a + b)4 – (a – b)4. Hence, evaluate (√3 + √2)4 – (√3 – √2)4.
Solution:
According to Theorem 1, we have
(a + b)4 = 4C0 a4 + 4C1 a3 b + 4C2 a2 b2 + 4C3 a b3 + 4C4 b4
According to Theorem 2, we have
(a – b)4 = 4C0 a4 – 4C1 a3 b + 4C2 a2 b2 – 4C3 a b3 + 4C4 b4
Now, (a + b)4 – (a – b)4
= 4C0 a4 + 4C1 a3 b + 4C2 a2 b2 + 4C3 a b3 + 4C4 b4 – [4C0 a4 – 4C1 a3 b + 4C2 a2 b2 – 4C3 a b3 + 4C4 b4]
= 2 (4C1 a3 b + 4C3 a b3)
= 2 (4a3 b + 4ab3)
= 8ab (a2 + b2) -(1)
Now, according to Equation(1), we get
a = √3 and b = √2
So, (√3 + √2)4 – (√3 – √2)4
= 8 × √3 × √2 ((√3)2 + (√2)2)
= 8 (√6)(3 + 2)
= 40 √6
Question 12. Find (x + 1)6+ (x – 1)6. Hence or otherwise evaluate (√2 + 1)6 + (√2 – 1)6.
Solution:
According to Theorem 1, , we have
(x + 1)6 = 6C0 x6 + 6C1 x5 + 6C2 x4 + 6C3 x3 + 6C4 x2 + 6C5 x + 6C6
According to Theorem 2, , we have
(x – 1)6 = 6C0 x6 – 6C1 x5 + 6C2 x4 – 6C3 x3 + 6C4 x2 – 6C5 x + 6C6
Now, (x + 1)6 – (x – 1)6
= 6C0 x6 + 6C1 x5 + 6C2 x4 + 6C3 x3 + 6C4 x2 + 6C5 x + 6C6 – [6C0 x6 – 6C1 x5 + 6C2 x4 – 6C3 x3 + 6C4 x2 – 6C5 x + 6C6]
= 2 [6C0 x6 + 6C2 x4 + 6C4 x2 + 6C6]
= 2 [x6 + 15x4 + 15x2 + 1] -(1)
Now, According to Equation(1),
x = √2
So, (√2 + 1)6 – (√2 – 1)6
= 2 [(√2)6 + 15(√2)4 + 15(√2)2 + 1]
= 2 (8 + (15 × 4) + (15 × 2) + 1)
= 2 (8 + 60 + 30 + 1)
= 2 (99)
= 198
Question 13. Show that 9n+1 – 8n – 9 is divisible by 64, whenever n is a positive integer.
Solution:
To Prove: 9n+1 – 8n – 9 = 64 k, where k is some natural number
According to Theorem 1, we have
For a = 1, b = 8 and m = n + 1 we get,
(1 + 8)n+1 = n + 1C0 + n + 1C1 (8) + n + 1C2 (8)2 + …. + n+1 C n+1 (8)n+1
9n+1 = 1 + (n + 1) 8 + 82 [n+1C2 + n+1C3 (8) + …. + n+1 C n+1 (8)n+1]
9n+1 = 9 + 8n + 64 [n+1C2 + n+1C3 (8) + …. + n+1 C n+1 (8)n+1]
9n+1 – 8n – 9 = 64 k
Where k, will be a natural number
Hence, proved 9n+1 – 8n – 9 is divisible by 64, whenever n is positive integer.
Question 14. Prove that 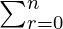 3r nCr = 4n
3r nCr = 4n
Solution:
As, we know that According to Binomial Theorem,
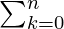 nCk an-k bk = (a + b)n
nCk an-k bk = (a + b)n
By comparing Theorem 1 with question, we get
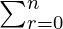 3r nCr = 4n
3r nCr = 4n
a + b = 4, k = r and b = 3
a = 1.
So, 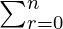 nCr an-r br = (a+b)n
nCr an-r br = (a+b)n
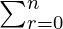 nCr 1n-r 3r = (1+3)n
nCr 1n-r 3r = (1+3)n
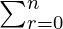 nCr (1) 3r = 4n
nCr (1) 3r = 4n
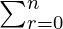 nCr 3r = 4n
nCr 3r = 4n
Hence, Proved
Share your thoughts in the comments
Please Login to comment...