Class 11 NCERT Solutions- Chapter 12 Introduction to three dimensional Geometry – Miscellaneous Exercise on Chapter 12
Last Updated :
12 Mar, 2021
Question 1: Three vertices of a parallelogram ABCD are A(3, – 1, 2), B (1, 2, – 4), and C (– 1, 1, 2). Find the coordinates of the fourth vertex.
Solution:
ABCD is a parallelogram, with vertices A (3, -1, 2), B (1, 2, -4), C (-1, 1, 2) and D (x, y, z).

Using the property:
The diagonals of a parallelogram bisect each other,
Midpoint of AC = Midpoint of BD = Point O
Now, by using Midpoint section formula
Coordinates of O for the line segment joining (x1,y1,z1) and (x2,y2,z2) = 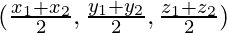
So, Coordinates of O for the line segment joining AC = 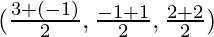
= 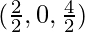
= (1, 0, 2) ……………………….(1)
and, Coordinates of O for the line segment joining BD = 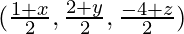 ………….(2)
………….(2)
Using the Eq(1) and Eq(2), we get
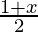 = 1
= 1
x = 1
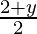 = 0
= 0
y = -2
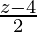 = 2
= 2
z = 8
Hence, the coordinates of the fourth vertex is D (1, -2, 8).
Question 2: Find the lengths of the medians of the triangle with vertices A (0, 0, 6), B (0,4, 0), and (6, 0, 0).
Solution:
The vertices of the triangle are A (0, 0, 6), B (0, 4, 0) and C (6, 0, 0).
So, let the medians be AD, BE and CF corresponding to the vertices A, B and C respectively.
D, E and F are the midpoints of the sides BC, AC and AB respectively.

Coordinates of mid-point for the line segment joining (x1,y1,z1) and (x2,y2,z2) = 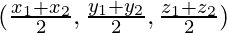
So, Coordinates of D for the line segment joining BC = 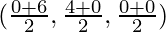
Coordinates of D = (3, 2, 0)
and, Coordinates of E for the line segment joining AC = 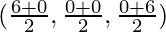
Coordinates of E = (3, 0, 3)
and, Coordinates of F for the line segment joining AB = 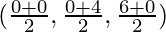
Coordinates of F = (0, 2, 3)
By using the distance formula for two points, P(x1,y1,z1) and Q(x2,y2,z2)
PQ = 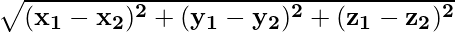
So, AD = 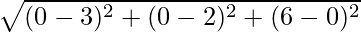
AD =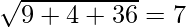
and, BE = 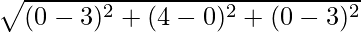
BE = 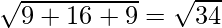
and, CF = 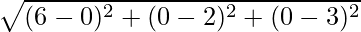
CF = 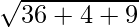 = 7
= 7
Hence, the lengths of the medians are 7, √34 and 7.
Question 3: If the origin is the centroid of the triangle PQR with vertices P (2a, 2, 6), Q (– 4, 3b, –10), and R(8, 14, 2c), then find the values of a, b and c.
Solution:
The vertices of the triangle are P (2a, 2, 6), Q (-4, 3b, -10) and R (8, 14, 2c).

Coordinates of centroid(0, 0, 0) of the triangle having vertices (x1,y1,z1), (x2,y2,z2) and (x3,y3,z3) = 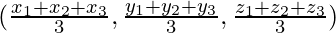
(0, 0, 0) =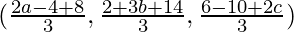
(0, 0, 0) = 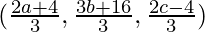
So, 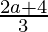 = 0
= 0
a = -2
and, 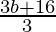 = 0
= 0
b = 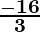
and, 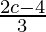 = 0
= 0
c = 2
Hence, the values of a, b and c are a = -2, b = 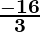 and c = 2
and c = 2
Question 4: Find the coordinates of a point on y-axis which are at a distance of 5√2 from the point P (3, –2, 5).
Solution:
Point on y-axis = A (0, y, 0).
Distance between the points A (0, y, 0) and P (3, -2, 5) = 5√2.
Now, by using distance formula,
Distance of PQ = 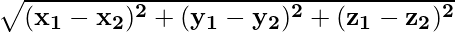
So, the distance between the points A (0, y, 0) and P (3, -2, 5) will be
Distance of AP = √[(3-0)2 + (-2-y)2 + (5-0)2]
= √[32 + (-2-y)2 + 52]
= √[(-2-y)2 + 9 + 25]
5√2 = √[(-2-y)2 + 34]
Squaring on both the sides, we get
(-2 -y)2 + 34 = 25 × 2
(-2 -y)2 = 50 – 34
4 + y2 + (2 × -2 × -y) = 16
y2 + 4y + 4 -16 = 0
y2 + 4y – 12 = 0
y2 + 6y – 2y – 12 = 0
y (y + 6) – 2 (y + 6) = 0
(y + 6) (y – 2) = 0
y = -6, y = 2
Hence, the points (0, 2, 0) and (0, -6, 0) are the required points on the y-axis.
Question 5: A point R with x-coordinate 4 lies on the line segment joining the points P(2, –3, 4) and Q (8, 0, 10). Find the coordinates of the point R.
[Hint: Suppose R divides PQ in the ratio k : 1. The coordinates of the point R are given by 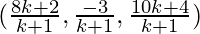 ]
]
Solution:
Let the coordinates of the required point be (4, y, z).
So now, let the point R (4, y, z) divides the line segment joining the points P (2, -3, 4) and Q (8, 0, 10) in the ratio k: 1.
Coordinates of the point which divides PQ in the ratio k : 1 = 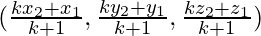
So, we have
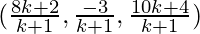 = (4, y, z)
= (4, y, z)
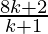 = 4
= 4
8k + 2 = 4 (k + 1)
8k + 2 = 4k + 4
8k – 4k = 4 – 2
4k = 2
k = 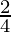
k = 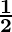
Now, substituting the value we get,
y = 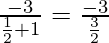 = -2
= -2
z = 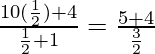 = 6
= 6
Hence, the coordinates of the required point are (4, -2, 6).
Question 6: If A and B be the points (3, 4, 5) and (–1, 3, –7), respectively, find the equation of the set of points P such that PA2 + PB2 = k2, where k is a constant.
Solution:
The points A (3, 4, 5) and B (-1, 3, -7)
Let the point be P (x, y, z).
Now by using distance formula,
Distance of point (x1, y1, z1) and (x2, y2, z2) = 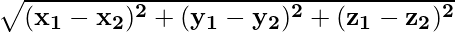
So, the distance between the points A (3, 4, 5) and P (x,y,z)) will be
Distance of PA = √[(3-x)2 + (4-y)2 + (5-z)2]
Distance of PB = √[(-1-x)2 + (3-y)2 + (-7-z)2]
As, PA2 + PB2 = k2
[(3 – x)2 + (4 – y)2 + (5 – z)2] + [(-1 – x)2 + (3 – y)2 + (-7 – z)2] = k2
[(9 + x2 – 6x) + (16 + y2 – 8y) + (25 + z2 – 10z)] + [(1 + x2 + 2x) + (9 + y2 – 6y) + (49 + z2 + 14z)] = k2
9 + x2 – 6x + 16 + y2 – 8y + 25 + z2 – 10z + 1 + x2 + 2x + 9 + y2 – 6y + 49 + z2 + 14z = k2
2x2 + 2y2 + 2z2 – 4x – 14y + 4z + 109 = k2
2x2 + 2y2 + 2z2 – 4x – 14y + 4z = k2 – 109
2 (x2 + y2 + z2 – 2x – 7y + 2z) = k2 – 109
(x2 + y2 + z2 – 2x – 7y + 2z) = 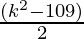
Hence, the required equation is (x2 + y2 + z2 – 2x – 7y + 2z) = 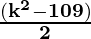
Share your thoughts in the comments
Please Login to comment...