Question 1. Find the values of k for which the line (k – 3)x – (4 – k2)y + k2 – 7k + 6 = 0 is
(a) Parallel to the x-axis
(b) Parallel to the y-axis
(c) Passing through the origin.
Solution:
We are given the line, (k – 3)x – (4 – k2)y + k2 – 7k + 6 = 0
=> (4 – k2)y = (k – 3)x + k2 – 7k + 6
=> y =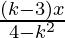 +
+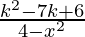
Now the equation of the line is of the form y = mx + c where m is the slope of the line and c is its y-intercept.
So, we get m =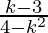 and c =
and c =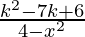
(a) Parallel to the x-axis
If the line is parallel to the x-axis, then we have,
Slope of the line = Slope of the x-axis
=> m = 0
=>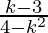 = 0
= 0
=> k – 3 = 0
=> k = 3
Therefore, if the given line is parallel to the x-axis, then the value of k is 3.
(b) Parallel to the y-axis
If the line is parallel to the y-axis, then we have,
Slope of the line = Slope of the y-axis
=> m = ∞ (undefined)
=>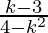 = ∞
= ∞
=> k2 − 4 = 0
=> k2 = 4
=> k = ±2
Therefore, if the given line is parallel to the y-axis, then the value of k is ± 2.
(c) Passing through the origin.
If the line is passing through the origin,
Y-intercept = 0
=> c = 0
=> k2 – 7k + 6 = 0
=> (k – 6) (k – 1) = 0
=> k = 1 or k = 6
Therefore, if the given line is passing through the origin, then the value of k is either 1 or 6.
Question 2. Find the values of θ and p, if the equation x cos θ + y sin θ = p is the normal form of the line √3x + y + 2 = 0.
Solution:
We are given the line, √3x + y + 2 = 0.
=> −√3x − y = 2
On converting this into normal form, we get
=>
=>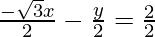
=>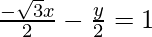
By comparing this equation with the given normal form x cos θ + y sin θ = p, we get
=> cos θ =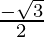 , sin θ =
, sin θ = and p = 1
and p = 1
The values of sin θ and cos θ are negative. So, θ = π +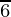 =
=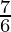 .
.
Therefore, the value of θ is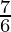 and p is 1.
and p is 1.
Question 3. Find the equations of the lines, which cut-off intercepts on the axes whose sum and product are 1 and –6, respectively.
Solution:
Let’s suppose the intercepts cut by the given lines on the axes are a and b. According to the question, we have,
=> a + b = 1 . . . . (1)
=> ab = – 6 . . . . (2)
By solving both the equations we get
a = 3 and b = –2 or a = –2 and b = 3
We know that the equation of the line whose intercepts are a and b axes is,
bx + ay – ab = 0
When a = 3 and b = –2
So the equation of the line is – 2x + 3y + 6 = 0, i.e. 2x – 3y = 6.
When a = –2 and b = 3
So the equation of the line is 3x – 2y + 6 = 0, i.e. –3x + 2y = 6.
Therefore, the required equation of the lines are 2x – 3y = 6 and –3x + 2y = 6.
Question 4. What are the points on the y-axis whose distance from the line x/3 + y/4 = 1 is 4 units?
Solution:
Suppose (0, b) is the point on the y-axis whose distance from line x/3 + y/4 = 1 is 4 units.
The line can be written as 4x + 3y – 12 = 0
By comparing our equation to the general equation of line Ax + By + C = 0, we get
A = 4, B = 3 and C = –12
Now, we know that the perpendicular distance(d) of a line Ax + By + C = 0 from (x1, y1) is given by,
d =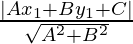
We are given d = 4. For the point (0, b), the value of d becomes,
=>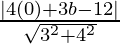 = 4
= 4
=>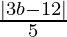 = 4
= 4
=> |3b – 12| = 20
=> 3b – 12 = 20 or 3b – 12 = –20
=> b = 32/3 or b = –8/3
Therefore, (0, 32/3) and (0, –8/3) are the points on the y-axis whose distance from the line x/3 + y/4 = 1 is 4 units.
Question 5. Find the perpendicular distance from the origin to the line joining the points (cos θ, sin θ) and (cos Ø, sin Ø).
Solution:
The equation of the line joining the points (cos θ, sin θ) and (cos Ø, sin Ø) is given by,
=> y – sin θ =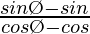 (x – cosθ)
(x – cosθ)
=> y(cos Ø – cos θ) – sin θ(cos Ø – cos θ) = x(sin Ø – sin θ) – cos θ(sin Ø – sin θ)
=> x(sin Ø – sin θ) + y(cos Ø – cos θ) + cos θ sin Ø – sin θ cos θ – sin θ cos Ø + sin θ cos θ = 0
=> x(sin Ø – sin θ) + y(cos Ø – cos θ) + sin (Ø – θ) = 0
So, we get, A = sin Ø – sin θ, B = cos Ø – cos θ and C = sin (Ø – θ).
Now, we know that the perpendicular distance(d) of a line Ax + By + C = 0 from the origin (0, 0) is given by,
d =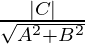
=
=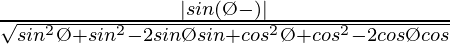
=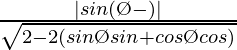
=
=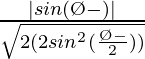
=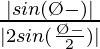
Therefore,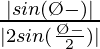 is the perpendicular distance from the origin to the given line.
is the perpendicular distance from the origin to the given line.
Question 6. Find the equation of the line parallel to y-axis and drawn through the point of intersection of the lines x – 7y + 5 = 0 and 3x + y = 0.
Solution:
Two given lines are
x – 7y + 5 = 0 . . . . (1)
3x + y = 0 . . . . (2)
By solving equations (1) and (2) we get
x = −5/22 and y = 15/22
(−5/ 22, 15/22) is the point of intersection of lines (2) and (3)
Now the equation of any line parallel to the y-axis is of the form
x = a . . . . (1)
If the line x = a passes through point (−5/22, 15/22) we get a = −5/22.
Therefore, the required equation of the line is x = −5/22.
Question 7. Find the equation of a line drawn perpendicular to the line x/4 + y/6 = 1 through the point, where it meets the y-axis.
Solution:
Given line is, x/4 + y/6 = 1.
=> 3x + 2y – 12 = 0
=> y = −3/2 x + 6, which is of the form y = mx + c
Here the slope of the given line = −3/2
So the slope of line perpendicular to the given line = −1/(−3/2) = 2/3
Suppose the given line intersects the y-axis at (0, y). So, the equation of the given line becomes,
=> y/6 = 1
=> y = 6
Hence, the given line intersects the y-axis at (0, 6). We know that the equation of the line that has a slope of 2/3 and passes through point (0, 6) is given by,
=> (y – 6) = 2/3 (x – 0)
=> 3y – 18 = 2x
=> 2x – 3y + 18 = 0
Therefore, the required equation of the line is 2x – 3y + 18 = 0.
Question 8. Find the area of the triangle formed by the lines y – x = 0, x + y = 0 and x – k = 0.
Solution:
It is given that
y – x = 0 . . . . (1)
x + y = 0 . . . . (2)
x – k = 0 . . . . (3)
Here the point of intersection of lines (1) and (2) is x = 0 and y = 0.
And the point of intersection of lines (2) and (3) is x = k and y = – k, lines (3) and (1) is x = k and y = k.
So the vertices of the triangle formed by the three given lines are (0, 0), (k, –k) and (k, k).
Here the area of triangle whose vertices are (x1, y1), (x2, y2) and (x3, y3) is
A =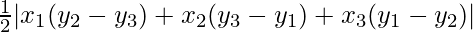
=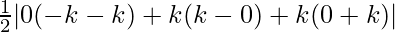
=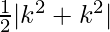
=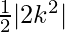
= k2 square units
Therefore, k2 sq. units is the area of the triangle formed by the given lines.
Question 9. Find the value of p so that the three lines 3x + y – 2 = 0, px + 2y – 3 = 0 and 2x – y – 3 = 0 may intersect at one point.
Solution:
It is given that
3x + y – 2 = 0 . . . . (1)
px + 2y – 3 = 0 . . . . (2)
2x – y – 3 = 0 . . . . (3)
By solving equations (1) and (3) we get
x = 1 and y = –1
It is given that the three lines intersect at one point and the point of intersection of lines (1) and (3) will also satisfy line (2).
=> p (1) + 2 (–1) – 3 = 0
=> p – 2 – 3 = 0
=> p = 5
Therefore, the value of p is 5.
Question 10. If three lines whose equations are y = m1x + c1, y = m2x + c2 and y = m3x + c3 are concurrent, then show that m1 (c2 – c3) + m2 (c3 – c1) + m3 (c1 – c2) = 0.
Solution:
It is given that
y = m1x + c1 . . . . (1)
y = m2x + c2 . . . . (2)
y = m3x + c3 . . . . (3)
By subtracting equation (1) from (2), we get,
=> 0 = (m2 – m1) x + (c2 – c1)
=> (m1 – m2) x = c2 – c1
=> x =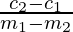
And y =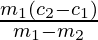 + c1
+ c1
=> y =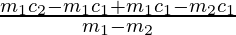
=> y =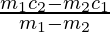
Hence, (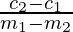 ,
,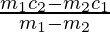 ) is the point of intersection of lines (1) and (2).
) is the point of intersection of lines (1) and (2).
As the given three lines are concurrent, this point must satisfy the equation (3).
=>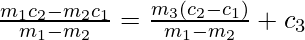
=>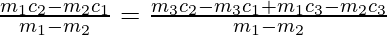
=>
=> m1 (c2 – c3) + m2 (c3 – c1) + m3 (c1 – c2) = 0
Hence proved.
Question 11. Find the equation of the lines through the point (3, 2) which makes an angle of 45° with the line x – 2y = 3.
Solution:
Suppose a is the slope of the line which passes through the point (3, 2).
Given line is x – 2y = 3.
y = 1/2 x – 3/2 which is of the form y = mx + c.
So, the slope of the given line b = 1/2
We know that the angle between the required line and line x – 2y = 3 is 45o. The angle is given by,
tan θ =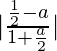
=> tan 450 =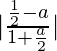
=>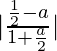 = 1
= 1
=>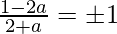
=> 2 + a = 1 – 2a or 2 + a = – 1 + 2a
=> a = –1/3 or a = 3
When a = 3, the equation of the line passing through (3, 2) and having a slope 3 is,
=> y – 2 = 3 (x – 3)
=> y – 2 = 3x – 9
=> 3x – y = 7
When a = –1/3, the equation of the line passing through (3, 2) and having a slope –1/3 is
=> y – 2 = –1/3 (x – 3)
=> 3y – 6 = – x + 3
=> x + 3y = 9
Therefore, the equations of the lines are 3x – y = 7 and x + 3y = 9.
Question 12. Find the equation of the line passing through the point of intersection of the lines 4x + 7y – 3 = 0 and 2x – 3y + 1 = 0 that has equal intercepts on the axes.
Solution:
Suppose the equation of the line having equal intercepts on the axes as
=> x/a + y/a = 1
=> x + y = a . . . . (1)
By solving equations 4x + 7y – 3 = 0 and 2x – 3y + 1 = 0, we get,
x = 1/13 and y = 5/13
(1/13, 5/13) is the point of intersection of two given lines.
Putting in (1), we get,
=> a = 1/13 + 5/13
=> a = 6/13
Here the equation (1) becomes
=> x + y = 6/13
=> 13x + 13y = 6
Therefore, the required equation of the line is 13x + 13y = 6.
Share your thoughts in the comments
Please Login to comment...