Different tests are used in statistics to compare distinct samples or groups and make conclusions about populations. These tests, also referred to as statistical tests, concentrate on examining the probability or possibility of acquiring the observed data under particular premises or hypotheses. They offer a framework for evaluating the evidence for or against a given hypothesis.
A statistical test starts with the formulation of a null hypothesis (H0) and an alternative hypothesis (Ha). The alternative hypothesis proposes a particular link or effect, whereas the null hypothesis reflects the default assumption and often states no effect or no difference.
The p-value indicates the likelihood of observing the data or more extreme results assuming the null hypothesis is true. Researchers compare the calculated p-value to a predetermined significance level, often denoted as α, to make a decision regarding the null hypothesis. If the p-value is smaller than α, the results are considered statistically significant, leading to the rejection of the null hypothesis in favor of the alternative hypothesis.
The p-value is calculated using a variety of statistical tests, including the Z-test, T-test, Chi-squared test, ANOVA, Z-test, and F-test, among others. In this article, we will focus on explaining the Z-test.
What is Z-Test?
Z-test is a statistical test that is used to determine whether the mean of a sample is significantly different from a known population mean when the population standard deviation is known. It is particularly useful when the sample size is large (>30).
Z-test can also be defined as a statistical method that is used to determine whether the distribution of the test statistics can be approximated using the normal distribution or not. It is the method to determine whether two sample means are approximately the same or different when their variance is known and the sample size is large (should be >= 30).
The Z-test compares the difference between the sample mean and the population means by considering the standard deviation of the sampling distribution. The resulting Z-score represents the number of standard deviations that the sample mean deviates from the population mean. This Z-Score is also known as Z-Statistics, and can be formulated as:
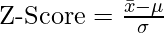
where,
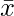 : mean of the sample.
: mean of the sample.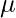 : mean of the population.
: mean of the population. : Standard deviation of the population.
: Standard deviation of the population.
z-test assumes that the test statistic (z-score) follows a standard normal distribution.
Example:
The average family annual income in India is 200k, with a standard deviation of 5k, and the average family annual income in Delhi is 300k.
Then Z-Score for Delhi will be.
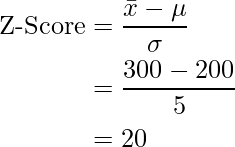
This indicates that the average family’s annual income in Delhi is 20 standard deviations above the mean of the population (India).
When to Use Z-test:
- The sample size should be greater than 30. Otherwise, we should use the t-test.
- Samples should be drawn at random from the population.
- The standard deviation of the population should be known.
- Samples that are drawn from the population should be independent of each other.
- The data should be normally distributed, however, for a large sample size, it is assumed to have a normal distribution because central limit theorem
Hypothesis Testing
A hypothesis is an educated guess/claim about a particular property of an object. Hypothesis testing is a way to validate the claim of an experiment.
- Null Hypothesis: The null hypothesis is a statement that the value of a population parameter (such as proportion, mean, or standard deviation) is equal to some claimed value. We either reject or fail to reject the null hypothesis. The null hypothesis is denoted by H0.
- Alternate Hypothesis: The alternative hypothesis is the statement that the parameter has a value that is different from the claimed value. It is denoted by HA.
Level of significance: It means the degree of significance in which we accept or reject the null hypothesis. Since in most of the experiments 100% accuracy is not possible for accepting or rejecting a hypothesis, we, therefore, select a level of significance. It is denoted by alpha (∝).
Steps to perform Z-test:
- First, identify the null and alternate hypotheses.
- Determine the level of significance (∝).
- Find the critical value of z in the z-test using
- Calculate the z-test statistics. Below is the formula for calculating the z-test statistics.
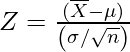
where,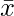 : mean of the sample.
: mean of the sample.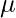 : mean of the population.
: mean of the population. : Standard deviation of the population.
: Standard deviation of the population.- n: sample size.
- Now compare with the hypothesis and decide whether to reject or not reject the null hypothesis
Type of Z-test
- Left-tailed Test: In this test, our region of rejection is located to the extreme left of the distribution. Here our null hypothesis is that the claimed value is less than or equal to the mean population value.
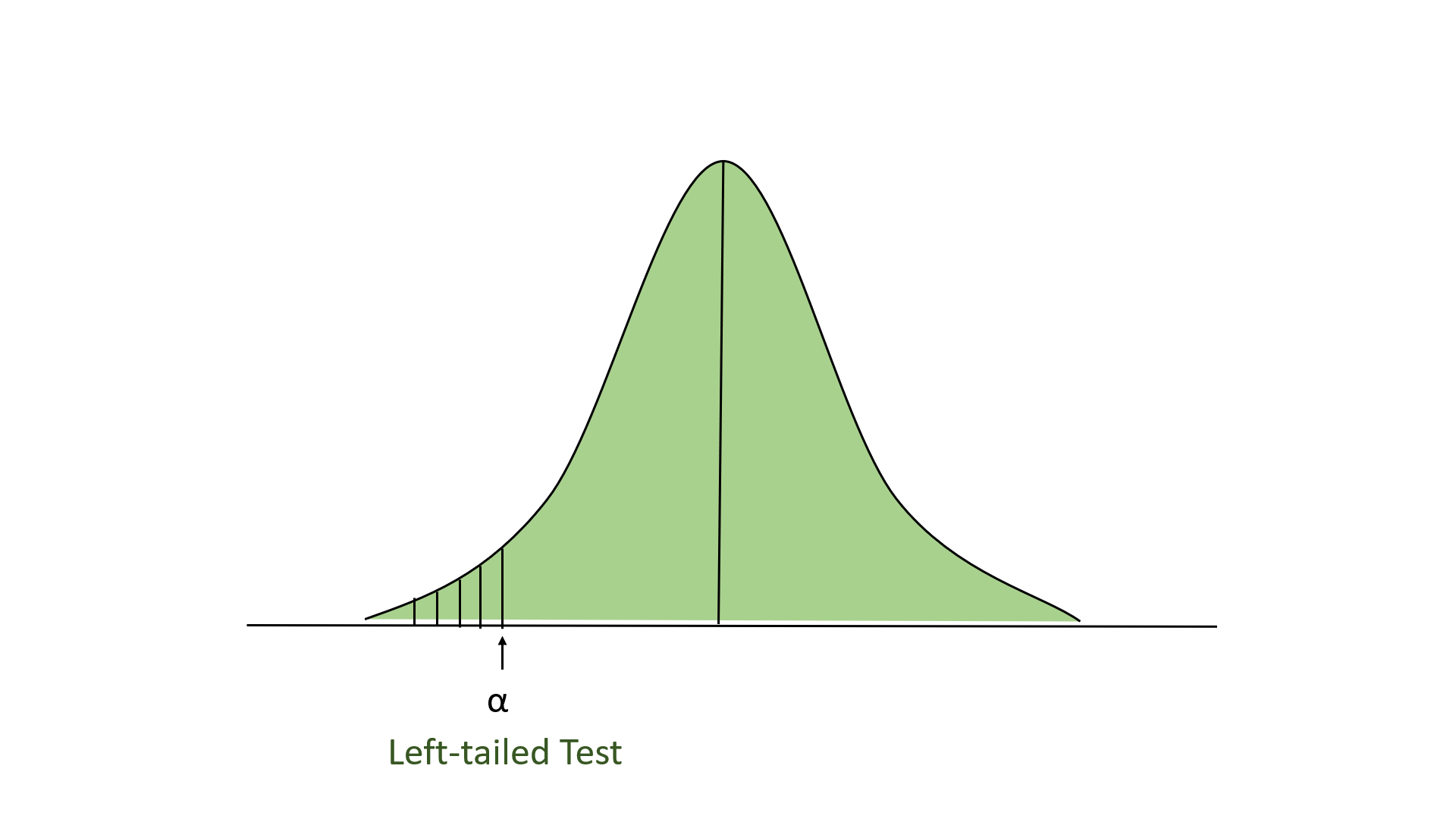
- Right-tailed Test: In this test, our region of rejection is located to the extreme right of the distribution. Here our null hypothesis is that the claimed value is less than or equal to the mean population value.
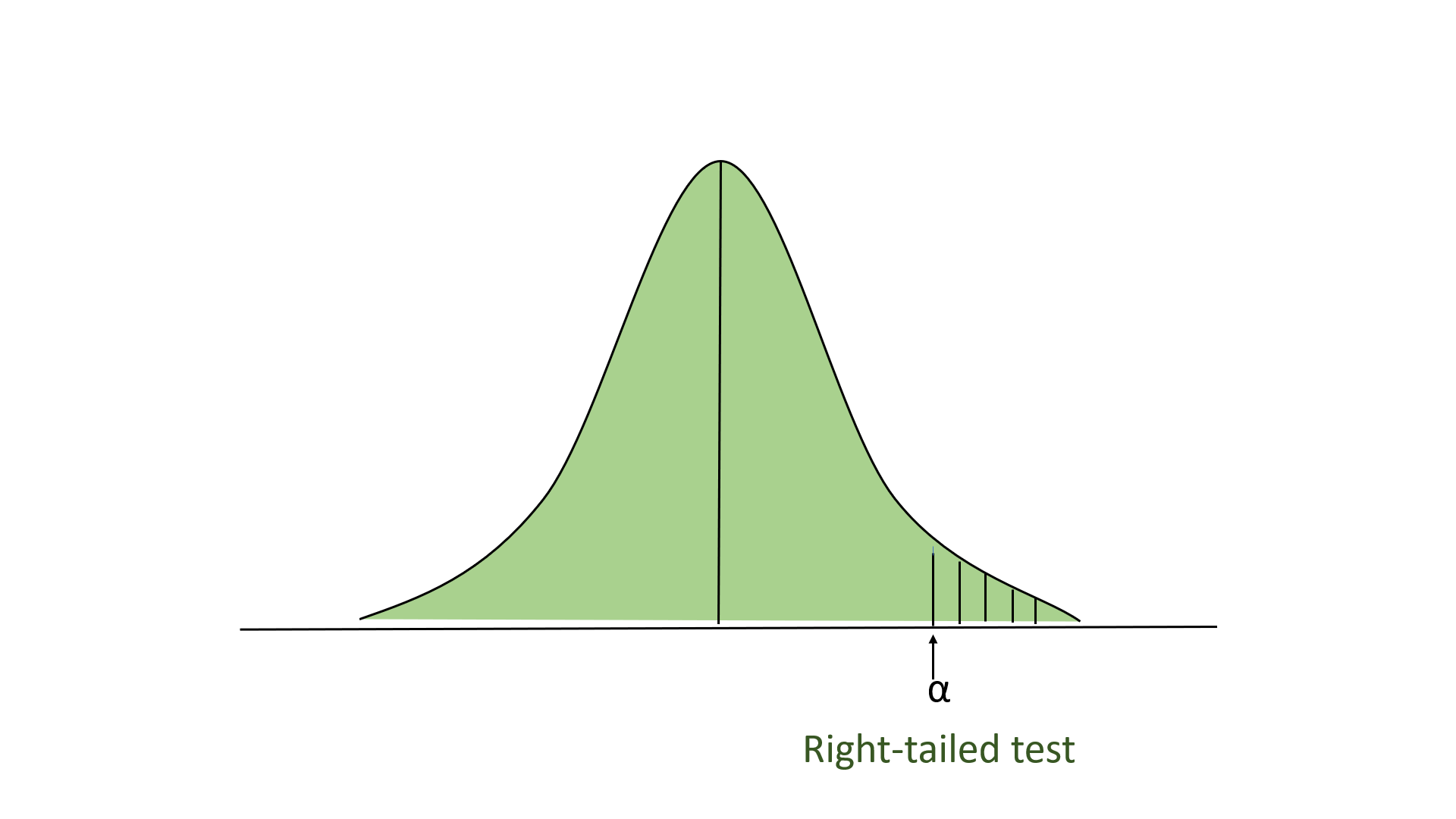
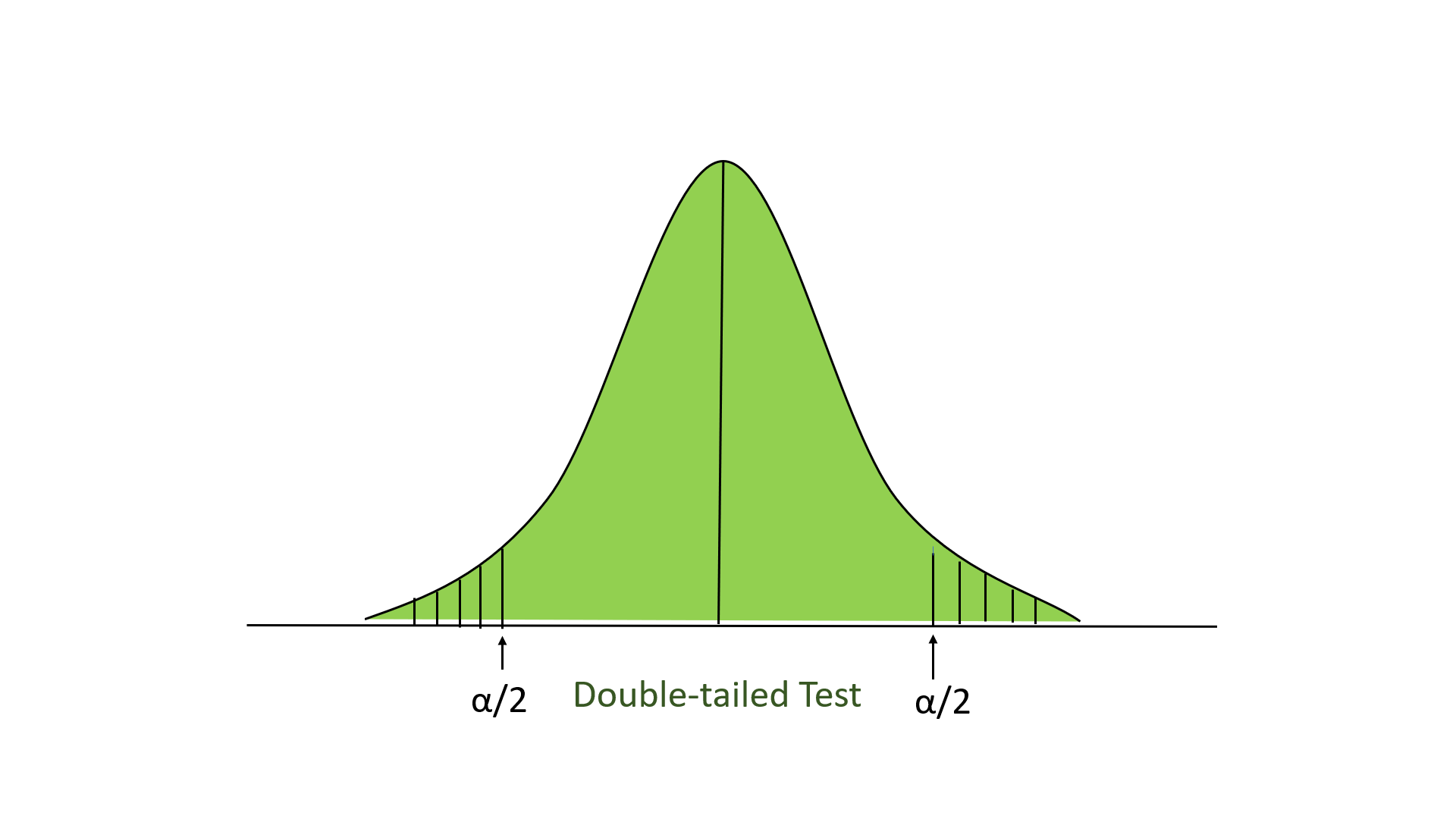
- Two-tailed test: In this test, our region of rejection is located to both extremes of the distribution. Here our null hypothesis is that the claimed value is equal to the mean population value.
Below is an example of performing the z-test:
Example One-Tailed Test:
A school claimed that the students who study that are more intelligent than the average school. On calculating the IQ scores of 50 students, the average turns out to be 110. The mean of the population IQ is 100 and the standard deviation is 15. State whether the claim of the principal is right or not at a 5% significance level.
- First, we define the null hypothesis and the alternate hypothesis. Our null hypothesis will be:
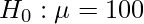
and our alternate hypothesis.
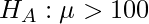
- State the level of significance. Here, our level of significance is given in this question (
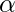 =0.05), if not given then we take ∝=0.05 in general.
=0.05), if not given then we take ∝=0.05 in general. - Now, we compute the Z-Score:
X = 110
Mean = 100
Standard Deviation = 15
Number of samples = 50
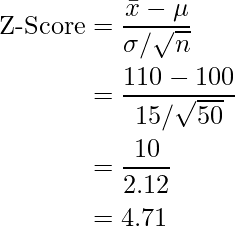
- Now, we look up to the z-table. For the value of ∝=0.05, the z-score for the right-tailed test is 1.645.
- Here 4.71 >1.645, so we reject the null hypothesis.
- If the z-test statistics are less than the z-score, then we will not reject the null hypothesis.
Code Implementations
Python3
import numpy as np
import scipy.stats as stats
sample_mean = 110
population_mean = 100
population_std = 15
sample_size = 50
alpha = 0.05
z_score = (sample_mean-population_mean)/(population_std/np.sqrt(50))
print('Z-Score :',z_score)
z_critical = stats.norm.ppf(1-alpha)
print('Critical Z-Score :',z_critical)
if z_score > z_critical:
print("Reject Null Hypothesis")
else:
print("Fail to Reject Null Hypothesis")
p_value = 1-stats.norm.cdf(z_score)
print('p-value :',p_value)
if p_value < alpha:
print("Reject Null Hypothesis")
else:
print("Fail to Reject Null Hypothesis")
|
Output:
Z-Score : 4.714045207910317
Critical Z-Score : 1.6448536269514722
Reject Null Hypothesis
p-value : 1.2142337364462463e-06
Reject Null Hypothesis
Two-sampled z-test:
In this test, we have provided 2 normally distributed and independent populations, and we have drawn samples at random from both populations. Here, we consider u1 and u2 to be the population mean, and X1 and X2 to be the observed sample mean. Here, our null hypothesis could be like this:
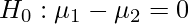
and alternative hypothesis
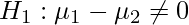
and the formula for calculating the z-test score:
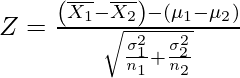
where 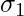 and
and 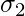 are the standard deviation and n1 and n2 are the sample size of population corresponding to u1 and u2 .
are the standard deviation and n1 and n2 are the sample size of population corresponding to u1 and u2 .
Example:
There are two groups of students preparing for a competition: Group A and Group B. Group A has studied offline classes, while Group B has studied online classes. After the examination, the score of each student comes. Now we want to determine whether the online or offline classes are better.
Group A: Sample size = 50, Sample mean = 75, Sample standard deviation = 10
Group B: Sample size = 60, Sample mean = 80, Sample standard deviation = 12
Assuming a 5% significance level, perform a two-sample z-test to determine if there is a significant difference between the online and offline classes.
Solution:
Step 1: Null & Alternate Hypothesis
- Null Hypothesis: There is no significant difference between the mean score between the online and offline classes
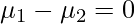
- Alternate Hypothesis: There is a significant difference in the mean scores between the online and offline classes.
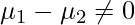
Step 2: Significance Label
- Significance Label: 5%
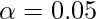
Step 3: Z-Score
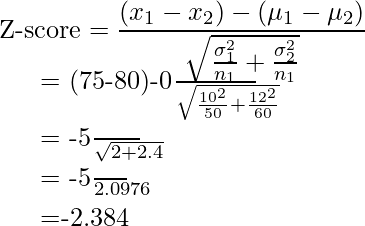
Step 4: Check to Critical Z-Score value in the Z-Table for apha/2 = 0.025
Step 5: Compare with the absolute Z-Score value
- absolute(Z-Score) > Critical Z-Score
- Reject the null hypothesis. There is a significant difference between the online and offline classes.
Code Implementations
Python3
import numpy as np
import scipy.stats as stats
n1 = 50
x1 = 75
s1 = 10
n2 = 60
x2 = 80
s2 = 12
D = 0
alpha = 0.05
z_score = ((x1 - x2) - D) / np.sqrt((s1**2 / n1) + (s2**2 / n2))
print('Z-Score:', np.abs(z_score))
z_critical = stats.norm.ppf(1 - alpha/2)
print('Critical Z-Score:',z_critical)
if np.abs(z_score) > z_critical:
print(
)
else:
print(
)
p_value = 2 * (1 - stats.norm.cdf(np.abs(z_score)))
print('P-Value :',p_value)
if p_value < alpha:
print(
)
else:
print(
)
|
Output:
Z-Score: 2.3836564731139807
Critical Z-Score: 1.959963984540054
Reject the null hypothesis.
There is a significant difference between the online and offline classes.
P-Value : 0.01714159544079563
Reject the null hypothesis.
There is a significant difference between the online and offline classes.
Type 1 error and Type II error:
- Type I error: Type 1 error has occurred when we reject the null hypothesis, even when the hypothesis is true. This error is denoted by alpha.
- Type II error: Type II error occurred when we didn’t reject the null hypothesis, even when the hypothesis is false. This error is denoted by beta.
|
Type I Error
(False Positive)
| Correct decision |
| Correct decision | Type II error
(False Negative)
|
Share your thoughts in the comments
Please Login to comment...