Points, Lines, and Planes are basic terms used in Geometry that have a specific meaning and are used to define the basis of geometry. We define a point as a location in 3-D or 2-D space that is represented using the coordinates.
We define a line as a geometrical figure that is extended in both directions to infinity. Similarly, a plane is defined as the collection of all such lines, i.e. it is a 3-D space on which the line passes.
In this article, we will learn about Points, Lines, and Planes in detail including their solved examples and problems based on them.
Points, Lines, and Planes in Geometry
In basic geometry, fundamental concepts like points, lines, and planes form the foundation upon which more complex geometric ideas are built. Points are precise locations in space, devoid of size or dimension, represented simply by dots. Lines are infinite paths stretching in two opposite directions, composed of an unending series of points. They are defined by any two distinct points lying on them. Beyond lines, planes extend infinitely in all directions, forming flat, two-dimensional surfaces. A plane can be defined by any three non-collinear points or by a line and a point not on the line. These basic elements serve as the starting point for exploring the intricacies of geometric shapes, relationships, and constructions.
What is a Point?
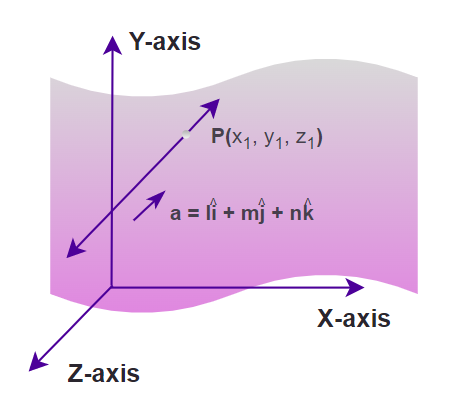
A Point in geometry is defined as a location in the space that is uniquely determined by an ordered triplet (x, y, z) where x, y, & z are the distances of the point from the X-axis, Y-axis, and Z-axis respectively in the 3-Dimensions and is defined by ordered pair (x, y) in the 2-Dimensions where, x and y are the distances of the point from the X-axis, and Y-axis, respectively. It is represented using the dot and is named using capital English alphabets. The figure added below shows a point P in the 3-D at a distance of x, y, and z from the X-axis, Y-axis, and Z-axis respectively.
Collinear points
We define collinear points as the points that lie on the same line, i.e. a straight line can be passed through the collinear point. Points A, B, and C shown in the image added below are the collinear points. For points to be collinear there must be a minimum of three points lying on the same line.
What is a Line?
A Line in three-dimensional geometry is defined as a set of points in 3D that extends infinitely in both directions It is the smallest distance between any two points either in 2-D or 3-D space. We represent a line with L and in 3-D space, a line is given using the equation,
L: (x – x1) / l = (y – y1) / m = (z – z1) / n
where
(x, y, z) are the position coordinates of any variable point lying on the line
(x1, y1, z1) are the position coordinates of a point P lying on the line
l, m, & n are the direction ratios of the line.
In 3D we can also form a line by the intersection of two non-parallel planes.
Points, Lines, and Planes
Line Segment
A line segment is defined as the finite length of the line that is used to join two points in 2-D and 3-D. It is the shortest distance between two points. A line segment between two points A and B is denoted as, AB
A line has infinite length whereas a line segment is a part of a line and has finite length.
Mid-Point
Midpoint is defined as the point on the line segment which divides the line segment into two equal parts. Suppose we have two points A and B and the line segment joining these two points is AB and not the point P on the line is called the midpoint if it breaks the line into two equal parts such that,
AP = PB
Thus, P is called the midpoint of line segment AB. The image added below shows the line segment AB with P as the midpoint.
Learn More: Mid-point Formula
Rays
A ray is defined as a line that has a fixed end point in one direction but can be extended to infinity in the other direction. It is of infinite length. We define the ray joining points O and A and extending to infinity towards A as
Intersecting and Parallel lines
In 2-D any two lines can either meet at some point or they never meet at some point. The lines that meet at some point are called intersecting lines. The distance between the intersecting line keeps on decreasing as we move toward the point of intersection, and at the point of intersection of these lines, the distance between them becomes zero. When two lines intersect an angle is formed between them.
Two lines that never meet each other in 2-D planes are called parallel lines. For parallel lines, the distance between them is always constant.
The images below show Intersecting and Parallel lines.
Perpendicular Lines
Intersecting lines that intersect at right angles are called perpendicular lines. The angle between these perpendicular lines is always the right angle or 90 degrees.
The perpendicular lines are shown in the image added below:
What is a Plane?
A Plane in three-dimensional (3D) geometry is a surface such that the line segment joining any two points lies completely on it. It is the collection of all the points and can be extended infinitely in any of the two dimensions.
The general form of a plane in 3D is a first-degree equation in x, y, z i.e. We represent a plane in 3-D as,
(ax + by + cz + d = 0)
where
(x, y, z) represents the coordinates of a variable point on the plane.
A plane has only two dimensions length and breadth and it can be infinitely stretched in these two dimensions.
Read More, Cartesian Plane
Solid
A solid is a 3-D concept we also called, space. We defined the solid as the extended plane that has three dimensions length breadth and height. A solid can be extended infinitely to incorporate all the space in 3-D.
The vector form of the equation of a plane in normal form is given by:
π: [Tex]{\vec {r}} [/Tex] . n̂ = d
where
π represents a plane in 3D space.[Tex]({\vec {r}} . {\vec{n}} = d) [/Tex]
[Tex]{\vec{r}} [/Tex]vector is the position vector of a general point lying on the plane,
n̂ is the unit vector normal to the plane
d is the distance of a plane from the origin
Note: The vector equation of the plane in the form [Tex]({\vec {r}} . {\vec{n}} = d) [/Tex] is said to be in the normal form only when [Tex]{\vec {n}} [/Tex]is a unit vector normal to the plane and d is the distance of the plane from the origin. If [Tex]{\vec {n}} [/Tex] is not a unit vector then we have to divide the above equation by [Tex] |{\vec{n}}| [/Tex] on both sides in order to convert it into the normal form. [Tex]{\vec {r}}.({\vec{n}}/|{\vec{n}}|) = d/|{\vec{n}}| or {\vec{r}}.n̂ = d/{\vec {|n|}} [/Tex]. This can be understood with the help of the example discussed below,
Example: The vector equation of the plane in 3D space which is at a distance of 8 units from the origin and normal to the vector (2 i+ j + 2 k) is given by?
Solution:
d = 8 and [Tex]{\vec {n}} [/Tex] = (2 i+ j + 2 k)
n̂ = (2 i+ j + 2 k) / √(22 + 12 + 22)
n̂ = (2 i+ j + 2 k) / √9
n̂ = (2/3) i+ (1/3) j + (2/3) k
Hence the required vector equation of the plane in normal form is
[Tex]{\vec {r}} [/Tex] . ((2/3) i+ (1/3) j + (2/3) k) = 8 which can be simplified as [Tex]{\vec {r}} [/Tex]. (2 i+ 1 j + 2 k) = 24
The cartesian form of the equation of a plane in normal form is given by:
π: lx + my + nz = p
where
π again represents a plane in 3D space
l, m, n are the DC’s i.e. direction cosines of the normal to the plane always satisfies this condition (l2 + m2 + n2 = 1)
p is the distance of the plane from the origin
Note: Any cartesian equation of the plane in the form (ax + by + cz + d = 0) is said to be in the normal form only when a, b, c are the direction cosines of the normal to the plane and |d| is the distance of the plane from the origin.
If a, b, and c are not the direction cosines of the normal to the plane then we have to follow these steps:
Step 1: Keep the terms of x, y, and z on the LHS and take the constant term d on the RHS.
Step 2: If the constant term on the RHS is negative then make it positive by multiplying with (-1) on both sides of the equation.
Step 3: Divide term on the both sides of the equation by √(a2 + b2 + c2).
After applying these steps the coefficients of x, y, and z on the LHS will become the direction cosines of the normal to the plane, and the constant term on the RHS will become the distance of the plane from the origin.
Example: A plane in the 3D space is represented by (2x + y + 2z – 24 = 0) then the cartesian equation of this plane in the normal form is given by.
Solution:
Given equation of plane,
2x + y + 2z = 24
Dividing both sides of the above equation by √(22 + 12 + 22) = √9 = 3
The given equation of plane in cartesian form is,
(2/3) x + (1/3) y + (2/3) z = 8
Here,
l = 2/3 , m = 1/3 , n = 2/3 are the direction cosines
p = 8 is the distance from the origin.
The distance of a point P (xo, yo, zo) from a plane π: (a x + b y + c z +d = 0) in the cartesian form is defined as the length (L) of the perpendicular drawn from that point to the plane. That is calculated using the formula,
L = |a xo + b yo + c zo + d| / √(a2 + b2 + c2)
Now let’s look at the example to know more.
Example: Find the distance of the point (2, 1, 0) from the plane (2 x + y + 2 z + 5 = 0).
Solution:
xo = 2, yo = 1, zo = 0
a = 2, b = 1, c = 2, d = 5
L = |(2 × 2) + (1 × 1) + (0 × 2) + 5| / √(22, 12, 22)
L = 10 / √9
L = 10/3
Thus, the required distance is 10/3 units.
The distance of a point P having position vector [Tex]{\vec {a}} [/Tex]from a plane π: [Tex]{\vec {r}}.{\vec {n}} = d [/Tex] in vector form is defined as the length (L) of the perpendicular drawn from that point to the plane.
L = [Tex]|{\vec {a}} . {\vec {n}}-d| / |{\vec {n}}|[/Tex]
Example: The distance of a point with position vector (2 i + j + 0 k) from the plane [Tex]{\vec {r}} [/Tex] . (2 i + j + 2 k) = 5 is given by?
Solution:
[Tex]{\vec {a}} [/Tex] = 2 i + j + 0 k
[Tex]{\vec {n}} [/Tex] = 2 i + j + 2 k
|[Tex]{\vec {n}} [/Tex]| = √(22, 12, 22) = √9 = 3
d = 5 (given)
[Tex]{\vec {a}}.{\vec {n}} [/Tex] = (2 × 2) + (1 × 1) + (0 × 2) = 5
L = |5 – 5| / 3
L = 0
Thus, the required distnce is 0 units.
People Also Read:
Points, Lines, and Planes Solved Examples
Example 1: The vector equation of the plane in 3D space which is at a distance of 5 units from the origin and normal to the vector (4 i+ 3 k) is given by?
Solution:
d = 5 and [Tex]{\vec {n}} [/Tex] = (4 i+ 3 k)
n̂ = (4 i + 3 k) / √(42 + 02 + 32)
n̂ = (4 i+ 3 k) / √(25)
n̂ = (4/5) i+ (3/5) k
Hence the required vector equation of the plane in normal form is,
[Tex]{\vec {r}} [/Tex] . ((4/5) i+ (3/5) k = 5
[Tex]{\vec {r}} [/Tex] . (4 i+ 3 k) = 25
Example 2: Find the distance of the point (0, 1, 0) from the plane (3 y + 4 z = 7).
Solution:
Given Point,
(xo, yo, zo) = (0, 1, 0)
xo = 0, yo = 1, zo = 0
Equation of the plane,
3 y + 4 z = 7
Comapring with ax + by +cz + d = 0
a = 0, b = 3, c = 4, d = -7
Distanc of a point form a plane is given using the formula,
L = |a xo + b yo + c zo + d| / √(a2 + b2 + c2)
L = |0 + (3 × 1) + (4 × 0) – 7| / √(02, 32, 42)
L = |3 – 7| / √(25)
L = 4/5
Thus, the required distance is 4/5 units
Example 3: Find the distance of a point (5, 3, 0) from the plane [Tex]{\vec {r}} [/Tex]. ( 4i + 3j) = 8.
Solution:
[Tex]{\vec {a}} [/Tex] = 5 i +3 j + 0 k
[Tex]{\vec {n}} [/Tex] = 4 i +3 j + 0 k
|[Tex]{\vec {n}} [/Tex]| = √(42+ 32+ 02)
= √(25) = 5
d = 8 (given)
[Tex]{\vec {a}} [/Tex] . [Tex]{\vec {n}} [/Tex] = (5 × 4) + (3 × 3) + (0 × 0)
= 29
L = |29 – 8| / 5
L = 21/5
Thus, the required distance is 21/5 units
Example 4: Find the distance between points, (2, 4) and (5, 6).
Solution:
Given point, (2, 4) and (5, 6)
Comapring with (x1, y1) and (x2, y2)
(x1, y1) = (2, 4) and (x2, y2) = (5, 6)
Using the distance formula,
d = √[(x2 – x1)2 + (y2 – y1)2]
d = √[(5-2)2 + (6-4)2]
= √13
Thus, the distance between two points is √13 units.
Points, Lines and Planes Worksheet
- Identify which of the following sets of points are collinear: A(2, 3), B(5, 7), C(8, 11).
- Determine if the points D(4, 6), E(4, 6), and F(4, 8) lie on the same line.
- Given three non-collinear points, how many distinct lines can be drawn through them?
- Determine whether the points G(2, 3, 1), H(4, 1, 3), and I(6, 5, 2) lie on the same plane.
- Find the equation of the line passing through the points P(2, 1) and Q(4, 5) in slope-intercept form.
- Determine the distance between the points R(3, 2, 4) and S(7, 5, 8).
FAQs on Points, Lines, and Planes
What is Geometry?
Geometry is the branch of mathematics that deals with the study of point, lines, planes, 2-D and 3-D surfaces and others. It gets its name from Greek word “Geo” meaning Earth and “Metron: meaning measurenment. This means Geometry means the study of Earth’s Measurment.
What is a Point?
A point is defined as the loctioan in 2-D or 3-D space that is defined using the co-ordinates in that space.
What is a Line?
A line is a gemetrical figure that joins two points and can be extended infinetely in both the directions.
What is a Plane?
We define plane as the infinite set of points that forms a connected flat surface and is exted in all the direction indinitely. It is a 2-D concept and all the lines are contained in the given plane.
What is a Space?
We define a space as the 3-D concept that is extended form of plane, it can be understood as the palne in 3-Dimensions it has three parameters length, breadtha nd height.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...