Sandwich Theorem

Sandwich Theorem also called Sandwich Rule or Squeeze Theorem, is an important theorem in calculus involving limits and it is used to find the limit of some functions when the normal methods of finding the limit fail. Suppose we have to find the limit such that lim_x->a f(x) gives an indeterminant form and solving the limit algebraically does not help then we find the limit of f(x) at a^– and a⁺ and if both the limits are equal then this limit also becomes the limit of f(x) at a. This is the sandwich theorem or squeeze theorem. 

The sandwich theorem is typically applied to confirm the limit of a function via comparison with two other functions whose limits are known or easily computed. Famous Greek mathematicians Archimedes was the first to use this concept. In this article, we will learn about Sandwich Theorem or Squeeze Theorem statement, its proof, examples, and others in detail.

Sandwich Theorem Definition

Sandwich theorem is one of the fundamental theorems of the limit. It is also known by the name Squeeze Theorem, it states that if any function f(x) exists between two other functions g(x) and h(x) and if the limit of g(x) and h(x) at any point (say a) are equal (say to L) then the limit of f(x) at a is also equal to L.

Sandwich Theorem Statement

Sandwich Theorem states that,

Let functions f(x), g(x), and h(x) be real values functions such that h(x) ≤ f(x) ≤ g(x). If 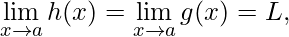 then  .

In the above situation, the function f(x) lies between h(x) and g(x), and hence h(x) and g(x) are called the lower bound and upper bound of f(x).

We can represent this condition easily using the graphs of the three functions h(x) ≤ f(x) ≤ g(x). The image added below shows the condition of the Sandwich Theorem.

Is Sandwich Theorem Always Zero

The sandwich theorem states that for two functions f(x) and g(x), if both of them approach the same limit say L, when x approaches a certain point, and there is a third function, h(x), such that f(x) ≤ h(x) ≤ g(x) for all x in some interval containing the point, then h(x) also approaches L as x approaches that point.

No the value of the sandwiched function is not always zero the sandwich function can have any of the values that the other function approaches not necessarily the value of the function that is used in the sandwich theorem can be any value.

Example: If given g(x) =  (x³ + 2)/(x) and  3x < (x³ + 2)/(x-2) < 4x, where x = 0

Now the value of g(x) at x = 0 does not exist.

But according to the Sandwich theorem,

3x  = 4x = 0 (at x = 0)

then, g(x) = 0 is also 0 at x = 0.

Sandwich Theorem Proof

To prove the sandwich theorem we can use the epsilon-delta definition of limit, which is called algebraic proof. The following heading shows detailed proof of the sandwich theorem using limits.

Algebraic Proof Using Definition of Limit

Sandwich theorem can be easily proved using the definition of limit. Assume three real-valued functions g(x), f(x), and h(x) such that g(x) ≤ f(x) ≤ h(x) and lim_x→a g(x) = lim_x→a h(x) = L. 

Then by the definition of limits,

lim_x→a g(x) = L signifies ∀ ∈ > 0, ∃ δ₁ > 0 such that |x – a| < δ₁ ⇒ |g(x) – L| < ∈

|x – a| < δ₁ ⇒ -∈ < g(x) – L < ∈   … (i)

lim_x→a h(x) = L signifies ∀ ∈ > 0, ∃ δ₂ > 0 such that |x – a| < δ₂ ⇒ |h(x) – L| < ∈

|x – a| < δ₂ ⇒ -∈ < h(x) – L < ∈    … (ii)

Given, g(x) ≤ f(x) ≤ h(x)

Subtracting L from each side of the inequality

g(x) – L ≤ f(x) – L ≤ h(x) – L

Taking δ = minimum {δ₁, δ₂}, Nowr |x – a| < δ,

-∈ < g(x) – L ≤ f(x) – L ≤ h(x) – L < ∈                 [using (i) and (ii)]

-∈ < f(x) – L < ∈

lim_x→a f(x) = L

Thus, this proved the Sandwich Theorem.

Geometric Proof of cos x < sin x/x < 1

We can understand the geometric proof of the statement cos x < sin x/x < 1, as follows

To Prove:  cos x < sin x/x < 1, for 0 < |x| < π/2

Also, using trigonometric identites

• sin (– x) = – sin x
• cos( – x) = cos x

We are now proving the inequality in eq(i)

Draw a unit circle with centre O

Now if ∠COA is x radians and 0 < x < π/2

For the figure,

Area of ΔOAC < Area of sector OAC < Area of Δ OAB

1/2×OA×CD < x/2π × π(OA)² < 1/2×OA×AB

Cancelling OA from each side

CD < x.OA < AB…(i)

In ΔOCD

sin x = CD/OC = CD/OA

CD = OA sin x…(ii)

Similarly, In ΔOAB

tan x = AB/OA

AB = OA tan x…(iii)

Now, from eq (i), (ii) and (iii) we get

sin x < x < tan x  [given 0<x<π/2]

Dividing sin x from each side

sin x/ sin x < x/(sin x) < tan x/ (sin x)

1 < x/(sin x) < 1/ (cos x)

Taking reciprocal,

cos x < (sin x)/(x) < 1

Thus, Proved.

Sandwich Theorem Limits

Some important limits which can be proved using Sandwich theorems are,

• lim_x→a (sin x / x) = 1
• lim_x→a (1-cos x / x) = 0

The proof of these limits are discussed below,

Proof of  lim_x→a (sin x / x) = 1

From the above inequality, we proved that

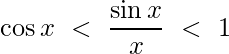
From this equation, we understand that (sin x/x) always lies between cos x and 1. So (sin x/x) is sandwiched between 1 and cos x. We know that

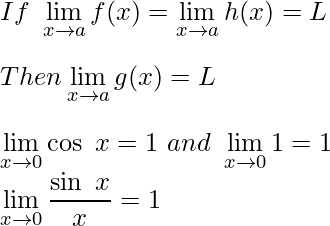
Proof of lim_x→a (1 – cos x)/x = 0

To prove this limit we use the trigonometric identity

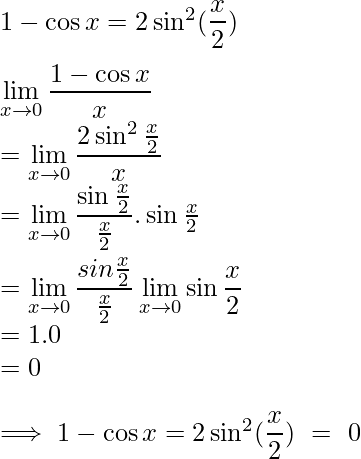
Sandwich Theorem Examples

Example 1: Find the value of lim_{x→ 0} f(x) if 9 – x² ≤ f(x) ≤ 9 + x²

Solution:

Now,

= lim_{x→ 0} 9 – x²
= 9 – 0²
= 9

= lim_{x→ 0} 9 + x²
= 9 + 0²
= 9

Now, if lim_{x→ 0} 9 – x² = lim_{x→ 0} 9 + x² = 9

Then using Sandwich Theorem we can say that,

lim_{x→ 0} 9 – x² = lim_{x→ 0} f(x) = lim_{x→ 0} 9 + x²

Thus the limit of lim_{x→ 0} f(x) = 9

Example 2: Find the limit lim_{x→ 0}  x² sin (1/x).

Solution:

As we know, the range of the sin function is [-1, 1] then,

-1 ≤ sin x ≤ 1

-1 ≤ sin (1/x) ≤ 1             (x ≠ 0)

Multiplying x² on each side

-x² ≤ x²sin (1/x) ≤ x²

Now, 

= lim_{x→ 0} -x²
= -0² = 0

= lim_{x→ 0} x²
= -0² = 0

Now, if lim_{x→ 0} – x² = lim_{x→ 0} x² = 0

Then using Sandwich Theorem we can say that,

lim_{x→ 0} – x² = lim_{x→ 0} x² sin (1/x) = lim_{x→ 0} x²

Thus the limit of lim_{x→ 0}  x² sin (1/x) = 0

FAQs on Sandwich Theorem

Q1: What is Sandwich Theorem?

Answer:

Sandwich Theorem or Squeeze Theorem is the basic theorem of the limit which is used to find the limit of the function when the limit of its upper bound and the lower bound is given and both are the same.

Q2: Why it is named Sandwich Theorem?

Answer:

This theorem is named Sandwich Theorem because it can be compared to a sandwich as in a sandwich the sauces and cheese are bound between two pieces of bread similarly in this theorem the function f(x) whose limit is to be found is bound between the two functions.

Q3: What are the other names of the Sandwich Theorem?

Answer:

The other name of the Sandwich Theorem is the Sandwich Rule or the Squeeze Theorem.

Q4: How do we apply Sandwich Theorem?

Answer:

We use the Sandwich theorem by,

For any real-valued functions f(x), g(x) and h(x) if they follow the condition g(x) ≤ f(x) ≤ h(x) then if,

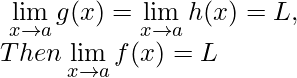
Q5: Who proposed Sandwich Theorem?

Answer:

The Sandwich Theorem also called Ham Sandwich Theorem was proposed by the famous mathematician called Hugo Steinhaus. Stefan Banach was the other famous mathematician who proved the Sandwich Theorem.