Mean Value Theorems (MVT) are the basic theorem used in mathematics. They are used to solve various types of problems in Mathematics. Mean Value Theorem is also called Lagrenges’s Mean Value Theorem. Rolle’s Theorem is a subcase of the mean value theorem and they are both widely used. These theorems are used to find the mean values of different functions. In this article, we will learn about Lagrange’s Mean Value Theorem, Rolle’s Theorem, their geometrical interpretations and others in detail.
Lagrange’s Mean Value Theorem
Lagrange’s Mean Value Theorem is used to find the mean value of any function in a defined interval. For any function f(x) that is defined on the closed interval [a, b] mean value theorem is applied if,
- f(x) is continuous in the closed interval [a, b]
- f(x) is differentiable in the open interval (a, b)
Then, according to Lagrange’s Mean Value Theorem, there exists at least one number c ∈ (a, b) such that
f'(c) = [f(b) – f(a)] / (b-a)
where, f'(c) is the differentiation of f(x) at point c.
This theorem is also called the “Mean Value Theorem or First Mean Value Theorem”
Geometrical Interpretation of Lagrange’s Mean Value Theorem
Geometrically speaking, the derivative at c denotes the slope of the tangent of at x = c for f(x). It says, there must exist a point in between that interval where the slope of the tangent is equal to the slope of the line joining points x = a and x = b.
Note: Lagrange’s Mean Value Theorem is also called Finite Mean Value Theorem as there can be any number of c-points in the interval (a, b)
Proof of Lagrange’s Mean Value Theorem
Statement:
According to Lagrange mean value theorem, “For a function f which is continuous over the closed interval [a,b], and differentiable over the open interval (a,b), there exists at least one point c in the interval (a,b) such that the slope of the tangent at the point c equals the slope of the secant through the endpoints of the curve which can be stated as,
f'(c) = f(b)−f(a ) / (b−a)
where, c ∈ (a, b)
Proof:
For any secant line g(x) to f(x) which passes through the points {a, f(a)} and {b, f(b)}. Now the slope of the secant line is given as,
m = {f(b)−f(a)} / (b−a)
Also the formula for the secant line is y-y1 = m (x- x1). Now, the equation of the secant line is given as,
y – f(a) = {f(b)−f(a)} / (b−a) × (x-a)
y = {f(b)−f(a)} / (b−a) × (x-a) + f(a)
As the equation of secant line is given as g(x) = y, now
g(x) = {f(b)−f(a)} / (b−a) × (x-a) + f(a)….(1)
Now, let’s define a function h(x) such that
h(x) = f(x) – g(x)
from eq (1)
h(x) = f(x) – [{f(b)−f(a)} / (b−a) × (x-a) + f(a)}
h(x) =- {f(b)−f(a)} / (b−a) × (x-a)
Now if the function h(x) is continuous on [a,b] and differentiable on (a,b). By applying the Rolles theorem, we get
h'(c) = 0 where, c ∈ (a, b)
h'(x) = f'(x) – [{f(b)−f(a)} / (b−a)]
Now, for some c in (a,b),
h'(c) = 0
f'(c) – {f(b)−f(a)} / (b−a) = 0
f'(c) = {f(b)−f(a)} / (b−a)
Thus the Lagrange mean value theorem has been proved.
Physical Interpretation of Lagrange’s Mean Value Theorem
Lagrange’s Mean Value Theorem, tells us the average change in function over the closed interval [a, b], whereas f'(c) can be interpreted as the instantaneous change at ‘c’. Thus, Lagrange’s Mean Value Theorem states that the average change in the function f(x) over the interval, [a, b] is equal to the instantaneous change f'(x) at point c for some c belonging to the interval (a, b).
Application of Lagrange’s Mean Value Theorem
Mean Value Theorem is known to be one of the most essential theorems in analysis and therefore, all its applications have major significance. Some of the applications are listed below:
- Leibniz’s Rule.
- L’ Hospital’s Rule.
- Strictly Increasing and Strictly decreasing functions.
- The symmetry of Second derivatives.
- The function is constant if f: (a, b)
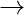 R is Differentiable and f'(x)=0 for all x∈(a, b).
R is Differentiable and f'(x)=0 for all x∈(a, b).
Example of Lagrange’s Mean Value Theorem
For the function f(x) = 2x2 – 4x + 5 defined in the interval [0, 2], verify Lagrange’s Mean Value Theorem
Solution:
Given,
a = 0 and b = 2
f(x) = 2x2 – 4x + 5
f'(x) = 4x – 4
f(a) = f(0) = 0
f(b) = f(2) = 2(2)2 – 4(2) + 5
= 5
Now,
[f(b) – f(a)]/ (b – a) = 5 – 0 / 2 – 0
= 5/2
we know that, f'(c) = [f(b) – f(a)]/ (b – a)
4c – 4 = 5/2
4c = 5/2 + 4
= 13/2
c = 13/8
c = 13/8 ∈ (0, 2)
Hence, Lagrange’s Mean Value Theorem is verified.
Rolle’s Theorem
Rolle’s Theorem is a special case of Lagrange’s Mean Value Theorem. It is also used to find the mean value of any function in a defined interval. It is applied when the initial value of the function f(a) equals the final value of the function f(b). For any function f(x) that is defined on the closed interval [a, b] Rolle’s Theorem is applied if,
- f(x) is continuous in the closed interval [a, b]
- f(x) is differentiable in the open interval (a, b)
- f(b) = f(a)
Then, according to Rolle’s Theorem, there exists at least one number c ∈ (a, b) such that
f'(c) = 0
where, f'(c) is the differentiation of f(x) at point c.
Geometric Interpretation of Rolle’s Theorem
Rolle’s Theorem states that if any function satisfies all the conditions of Rolle’s Theorem, i.e.
f(x) is continuous in the closed interval [a, b]
f(x) is differentiable in the open interval (a, b)
f(b) = f(a)
Then there exists f'(c) = 0, which means that the tangent at point c is parallel to the x-axis.
Note: It is not necessary that the converse of this theorem is also true. That is we cannot say if at some point f'(c) = 0 then all the conditions of Rolle’s theorem are satisfied.
Proof of Rolle’s Theorem
Statement:
According to, Rolle’s theorem,
Let a function f is taken such that, f : [a, b] → R be continuous on [a, b], differentiable on (a, b), and f(a) = f(b), for some real number a and b. Then there exists some c in the interval (a, b) such that f′(c) = 0.
Proof:
Taking the function f(x) which is,
- Continuous in the interval [a, b],
- Differentiable in the interval (a, b),
- And f(a) = f(b)
Now, for any function f(x) f′(x)=0 occurs at extreme values i.e. either at maxima or at minima.
Then, according to the Extreme Value Theorem theorem for any continuous function there exist both the maxima and minima in any finite interval.
Now, there exist two possibilities for our function,
Case 1: Function is constant.
Case 2: Function is not constant.
For, Case 1: Function is constant.
A constant function has a horizontal graph i.e. parallel to the x-axis which satisfies Rolle’s Theorem at all the points in the interval since the derivative is zero everywhere.
For, Case 2: Function is not constant.
As, the function is not constant and its initial value and final value are equal, i.e. f(a) = f(b) (given), it must change its direction at least once inside the interval. Thus, it is safe to assume that the function will either have a minimum, a maximum, or both.
Now we need to show that at any of the interior points, the derivative is equal to zero. The derivative of the function is zero either at maxima or minima. As, we have shown that the function will have either a minimum, a maximum, or both. It is safe to say that,
f'(c) = 0 for alteast some c in the interval (a, b).
Thus, Rolle’s Theorem is Verified.
Example of Rolle’s Theorem
For the function f(x) = 2x2 + 1 defined in the interval [-2, 2] verify Rolle’s Theorem.
Solution:
Given,
a = 0 and b = 2
f(x) = x2 + 1
f'(x) = 2x
f(a) = f(0) = 2(-2)2 + 1
= 9
f(b) = f(2) = 2(2)2 + 1
= 9
Now,
f(b) = f(a) thus condition for Rolle’s Theorem is verified.
we know that, f'(c) = 0
4c + 1 = 0
4c = -1
c = -1/4
c = -1/4 ∈ (-2, 2)
Hence, Rolle’s Theorem is verified.
Read More
Solved Example on Rolle’s and Lagrange’s Mean Value Theorem
Example 1: Find the value of “c” which satisfy the conclusion of the Mean Value Theorem for h(z) = 4z3 – 8z2 + 7z – 2 on [2,5].
Solution:
Since the function is a polynomial, so it is continuous and differentiable both in this interval. Thus mean value theorem can be applied here.
Given,
h(z) = 4z3 – 8z2 + 7z – 2
h(2) = 12
h(5) = 333
h'(z) = 12z2 -16z + 7
Now plug this into the formula of mean value theorem and solve for c.
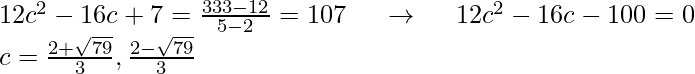
Example 2: Find the value of “c” which satisfy the conclusion of the Mean Value Theorem in the interval [-2,2] for f(x) = |x – 2| + |x|
Solution:
The given function, f(x) = |x – 2| + |x| is not differentiable. Thus mean value theorem cannot be applied on this function in the interval [-2, 2].
Example 3: Find the value of “c” which satisfy the conclusion of Mean Value Theorem in the interval for 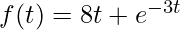 on [-2,3].
on [-2,3].
Solution:
This function is a sum of both exponential and polynomial functions. Since both the functions are continuous and differentiable everywhere, the function f(t) is continuous and differentiable everywhere. Thus mean value theorem is applicable.
f(-2) = -16 + e(-3 .-2) = -16 + e6
f(3) = 24 + e-9
f'(t) = 8 -3e-3t
Let’s plug it into the formula,
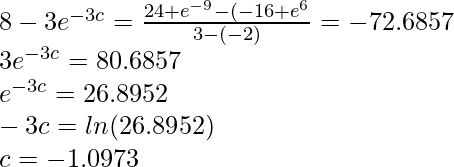
The value of c = -1.0973 ∈ (-2, 3) thus, Lagrange’s Mean value theorem is satisfied.
Example 4: Find the value of ‘c’ which satisfy Rolle’s theorem for f(x) = x2 – 2x – 8 on [-1, 3].
Solution:
Before finding out the points, we need to make sure that all the conditions of rolle’s theorem are applied on this interval.
This function is a polynomial, so it’s both differentiable and continuous on the interval.
Now let’s evaluate the function at the ends of the interval. f(-1) = -5 and f(3) = -5.
Function values are equal at both the ends. So, now all the conditions for rolle’s theorem are satisfied.
f'(x) = 2x – 2
f'(c) = 2c – 2 = 0
c = 1
The value of c = 1 ∈ (-1, 3) thus, Rolle’s theorem is satisfied.
Example 5: Examine if Rolle’s theorem is applicable for the functions f(x) = [x] for x ∈ [5, 9].
Solution:
This function is a step function, and is not continuous. So, Rolle’s Theorem is not applicable in the following interval.
FAQs on Lagrange’s Mean Value Theorem and Rolle’s Theorem
Question 1: What is the mean value theorem?
Answer:
Mean value theorem is a theorem which is used to find the mean of the given function. The mean value theorem formula is,
f'(c) = [f(b) – f(a)] / (b-a)
Question 2: How to find c in the mean value theorem?
Answer:
For any function f(x) defined on the interval [a, b] the value of c in the mean value theorem is calculated by using the formula,
f'(c) = [f(b) – f(a)] / (b-a)
where, f'(c) is differential of f(x) at point c.
Question 3: What are the conditions for Lagrange Mean Value Theorem?
Answer:
The condition For Lagrange Mean Value Theorem are, for any function f(x)
- f(x) should be continuous over the closed interval [a,b]
- f(x) should be differentiable over the open interval (a,b)
Question 4: What are the conditions for Rolle’s Theorem?
Answer:
The conditions for Rolle’s Theorem are, for any function f(x)
- f(x) should be continuous over the closed interval [a,b]
- f(x) should be differentiable over the open interval (a,b)
- f(b) = f(a)
Question 5: Is Rolle’s Theorem the same as Mean Value Theorem(MVT)?
Answer:
No, Rolle’s Theorem is not same as Mean Value Theorem. It is a special case of Mean Value Theorem which occurs when the value of function at initial point and the value of function at final point is same.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...