Puzzle | Farmer, Goat, Wolf and Cabbage
Last Updated :
18 Jan, 2023
There is a farmer who wishes to cross a river but he is not alone. He also has a goat, a wolf, and a cabbage along with him. There is only one boat available which can support the farmer and either of the goat, wolf or the cabbage. So at a time, the boat can have only two objects (farmer and one other).
But the problem is, if the goat and wolf are left alone (either in the boat or onshore), the wolf will eat the goat. Similarly, if the Goat and cabbage are left alone, then goat will eat the cabbage. The farmer wants to cross the river with all three of his belongings: goat, wolf, and cabbage.
What strategy he should use to do so?
Solution 1: Taking wolf on other side will leave goat and cabbage together. Also taking away cabbage will make wolf and goat be alone. Hence, the farmer will first take goat on the other side and return back alone. We have farmer, wolf, and cabbage at one side and goat on the other side.
Now, he will take the wolf along, drop the wolf on the other side and return with the goat. So now on one side, we have farmer, cabbage, and goat and on the other side, we have a wolf.
Now, he takes the cabbage along and returns alone. So now the scenario is: farmer, goat on one side and wolf, cabbage on the other side.
Now, finally, he crosses the river with the goat and hence succeeds in taking all his belongings with him.
Reference:https://www.bhavinionline.com/2013/10/river-crossing-puzzle-farmer-wants-to-cross-with-wolf-goat-and-cabbage/
Solution 2: This problem can be solved using graph theory .
Consider 2 states: initial (A) and final (B).
Initially, the right side of the river has nothing on it and the goat, cabbage, and wolf are on the left. And in the final state, all three (goat, cabbage, and wolf) will be on the right side. How can we reach state B from state A? The right bank can have these combinations of goat(G), cabbage(C), wolf(W).
-> 0, G, W, C, GW , GC , WC, GWC
0 represents the initial state (A) and GWC represents the final state(B). We can model this problem as an undirected weighted graph. Where each edge in the graph has weight 1 or infinite.
This graph can be used to represent our problem .
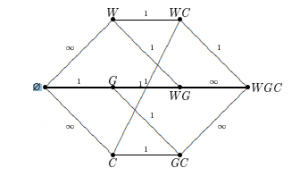
Now, all paths that have infinite weight cannot be traversed, else the problem’s constraints will be violated. So, we have to move from A to B using paths that have weight 1, and we can find a valid path using Dijkstra’s Shortest Path algorithm.
Explanation :
It is very clear that initially, the boatman can only take the goat with him. So, from vertex 0 to vertex G, we set the weight to 1. In other cases, (0 to W, 0 to C) someone will get eaten. Hence we set these weights to infinite.
Using similar intuition it is easy to devise the solution.
Share your thoughts in the comments
Please Login to comment...