Puzzle | 50 red marbles and 50 blue marbles
Last Updated :
18 Jan, 2023
Give two boxes
B1 and
B2 one have
50 red marbles and other have
50 blue marbles. A ball is selected randomly from any of the box and the task is to maximize the probability of selecting a red ball, by reshuffling marbles in both the boxes.
Solution:
Let
P(R) be the probability of picking a red marble.
P(R) = P(B1) * P(B1 | J1) + P(B2) * P(B2 | J2)
Here,
P(B1) and
P(B2) refers to selecting
B1 and
B2 and the probability of selecting each box is
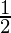 J1
J1 and
J2 refers to number of total balls in
B1 and
B2 respectively.
If we do not reshuffle any balls. Then
P(R) = ((1 / 2) * 1) + ((1 / 2) * 0) = 0.5
But, If we decrease the number of red balls in box B1 and increase the number of red balls in box B2 then the probability of getting a red ball will be maximized.
Therefore, let us take 49 red marbles from B1 to B2 then there will be 1 red ball in B1 and 99 balls in B2 out of which 49 are red and 50 of them are blue in the second jar.
Then
P (R) = ((1 / 2) * (1 / 1)) + ((1 / 2) * (49 / 99)) = 0.747474
Hence,
the maximum probability of choosing a red ball is 0.747474
Share your thoughts in the comments
Please Login to comment...