Puzzle 3 | (Calculate total distance travelled by bee)
Last Updated :
19 Jan, 2023
Puzzle: Two trains are on same track and they are coming toward each other. The speed of the first train is 50 km/h and the speed of the second train is 70 km/h. A bee starts flying between the trains when the distance between two trains is 100 km. The bee first flies from first train to second train. Once it reaches the second train, it immediately flies back to the first train … and so on until trains collide. Calculate the total distance travelled by the bee. Speed of bee is 80 km/h.
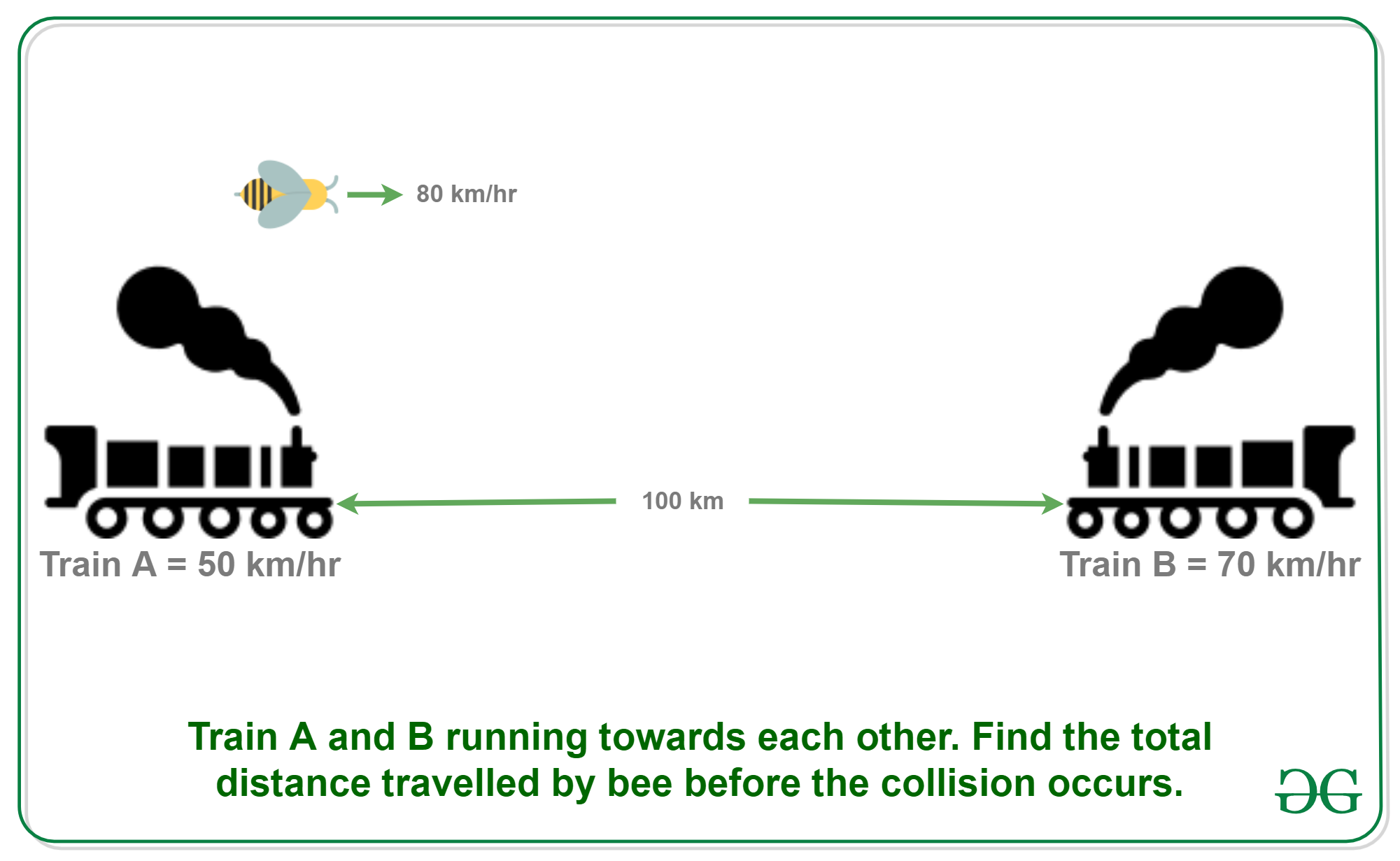
Answer: 66.67 km approx.
Solution:
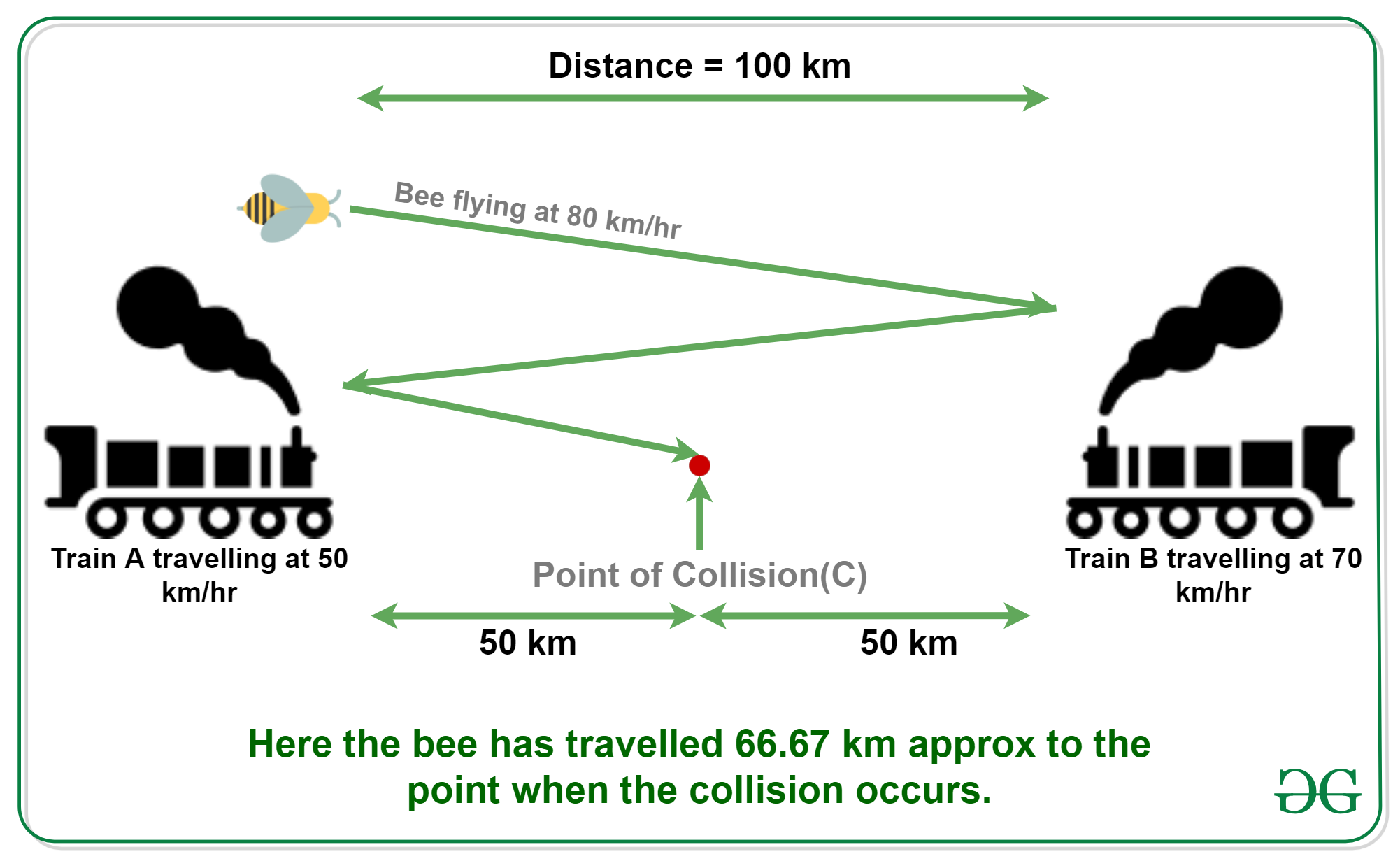
- Let the first train A move at u km/h.
- Let the second train B move at v km/h.
- Let the distance between two trains be d km
- Let the speed of bee be b km/h
- Therefore, the time taken by trains to collide = d/(u+v)
Now putting all the known values into the above equation, we get,
u = 50 km/hr
v = 70 km/hr
d = 100 km
b = 80 km/hr
Therefore, the total distance travelled by bee
= b*d/(u+v)
= 80 * 100/(50+70)
= 66.67 km (approx)
Another Solution:
Another easier approach to solve this can be by using the concept of relative velocity:
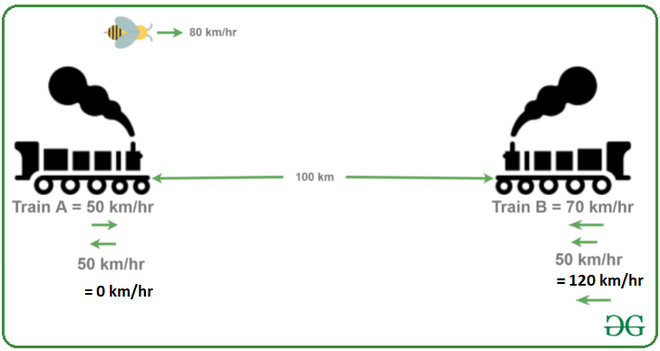
With respect to Train A, train B’s velocity is (70+50) = 120 km/hr. Thus, the time taken by Train B to collide with Train A will be
(100 km) / (120 km/hr) = 5/6 hr = 50 min
Now, since the velocity of the bee is 80 km/hr, the distance travelled by the bee in this time interval will be
80 km/hr * 5/6 hr = 66.67 km (approx)
Point to note –
The key point to note in this puzzle is that the bee will keep travelling from one train to another as it’s speed is greater than both the train’s speed. Thus we only need to find the time it takes for both the trains to collide and this time will be same as the time bee is flying and thus it has nothing to do with the point at which the trains collide.
Share your thoughts in the comments
Please Login to comment...