Solve the inequalities in Exercises 1 to 6.
Question 1. 2 ≤ 3x – 4 ≤ 5
Solution:
In this case, we have two inequalities, 2 ≤ 3x – 4 and 3x – 4 ≤ 5, which we will solve simultaneously.
We have 2 ≤ 3x – 4 ≤ 5
or 2 ≤ 3x – 4 and 3x – 4 ≤ 5
⇒ 2 + 4 ≤ 3x and 3x ≤ 5 + 4
⇒ 6 ≤ 3x and 3x ≤ 9
⇒ 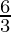 ≤ x and x ≤
≤ x and x ≤ 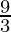
⇒ 2 ≤ x and x ≤ 3
⇒ 2 ≤ x ≤ 3
Hence, all real numbers x greater than or equal to 2 but less than or equal to 3 are solution of given 2 ≤ 3x – 4 ≤ 5 equality.
x ∈ [2, 3]
Question 2. 6 ≤ – 3 (2x – 4) < 12
Solution:
In this case, we have two inequalities, 6 ≤ – 3 (2x – 4) and – 3 (2x – 4) < 12, which we will solve simultaneously.
We have 6 ≤ – 3 (2x – 4) < 12
or 6 ≤ – 3 (2x – 4) and – 3 (2x – 4) < 12
⇒ 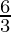 ≤ -(2x – 4) and -(2x – 4) <
≤ -(2x – 4) and -(2x – 4) < 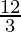
⇒ 2 ≤ -(2x – 4) and -(2x – 4) < 4
⇒ -2 ≥ (2x – 4) and (2x – 4) > -4 [multiplying the inequality with (-1) which changes the inequality sign]
⇒ -2+4 ≥ 2x and 2x > -4+4
⇒ 2 ≥ 2x and 2x > 0
⇒  ≥ x >
≥ x > 
⇒ 1≥ x > 0
⇒ 0 < x ≤ 1
Hence, all real numbers x greater than 0 but less than or equal to 1 are solution of given 6 ≤ – 3 (2x – 4) < 12 equality.
x ∈ (0, 1]
Question 3. -3 ≤ 4- 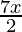 ≤ 18
≤ 18
Solution:
In this case, we have two inequalities, -3 ≤ 4- 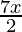 and 4-
and 4- 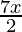 ≤ 18, which we will solve simultaneously.
≤ 18, which we will solve simultaneously.
We have -3 ≤ 4- 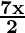 ≤ 18
≤ 18
or -3 ≤ 4- 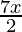 and 4-
and 4- 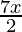 ≤ 18
≤ 18
⇒ -3-4 ≤ – 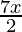 and –
and – 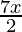 } ≤ 18-4
} ≤ 18-4
⇒ -7 ≤ – 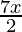 and –
and – 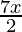 ≤ 14
≤ 14
⇒ 7 ≥ 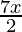 and
and 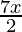 ≥ -14 [multiplying the inequality with (-1) which changes the inequality sign]
≥ -14 [multiplying the inequality with (-1) which changes the inequality sign]
⇒ 7×2 ≥ 7x and 7x ≥ -14×2
⇒ 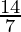 ≥ x and x ≥
≥ x and x ≥ 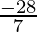
⇒ 2 ≥ x ≥ -4
⇒ -4 ≤ x ≤ 2
Hence, all real numbers x greater than or equal to -4 but less than or equal to 2 are solution of given -3 ≤ 4- 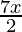 ≤ 18 equality.
≤ 18 equality.
x ∈ [-4, 2]
Question 4. -15 < 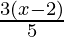 ≤ 0
≤ 0
Solution:
In this case, we have two inequalities, -15 < 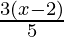 and
and 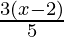 } ≤ 0, which we will solve simultaneously.
} ≤ 0, which we will solve simultaneously.
We have -15 < 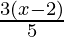 ≤ 0
≤ 0
or -15 < 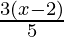 and
and 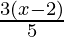 ≤ 0
≤ 0
⇒ -15×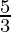 < (x-2) and (x-2) ≤ 0×
< (x-2) and (x-2) ≤ 0×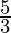
⇒ -25 < x-2 and x-2 ≤ 0
⇒ -25+2 < x and x ≤ 0+2
⇒ -23 < x ≤ 2
Hence, all real numbers x greater than -23 but less than or equal to 2 are solution of given -15 ≤ 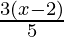 ≤ 0 equality.
≤ 0 equality.
x ∈ (-23, 2]
Question 5. -12 < 4- (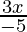 ) ≤ 2
) ≤ 2
Solution:
In this case, we have two inequalities, -12 < 4- 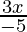 and 4-
and 4- 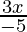 ≤ 2, which we will solve simultaneously.
≤ 2, which we will solve simultaneously.
We have -12 < 4- 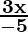 ≤ 2
≤ 2
or -12 < 4- 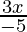 and 4-
and 4- 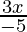 ≤ 2
≤ 2
⇒ -12-4 < 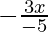 and
and 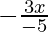 ≤ 2-4
≤ 2-4
⇒ -16 < 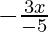 and
and 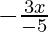 ≤ -2
≤ -2
⇒ -16 < 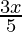 and
and 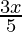 ≤ -2
≤ -2
⇒ -16×5 < 3x and 3x ≤ -2×5
⇒ 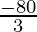 < x and x ≤
< x and x ≤ 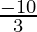
⇒ 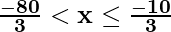
Hence, all real numbers x greater than -80/3 but less than or equal to -10/3 are solution of given -12 < 4- 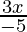 ≤ 2 equality.
≤ 2 equality.
x ∈ (-80/3, -10/3]
Question 6. 7 ≤ 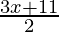 ≤ 11
≤ 11
Solution:
In this case, we have two inequalities, 7 ≤ 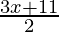 and
and 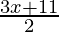 ≤ 11, which we will solve simultaneously.
≤ 11, which we will solve simultaneously.
We have 7 ≤ 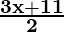 ≤ 11
≤ 11
or 7 ≤ 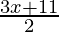 and
and 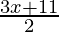 ≤ 11
≤ 11
⇒ 7×2 ≤ 3x+11 and 3x+11 ≤ 11×2
⇒ 14 ≤ 3x+11 and 3x+11 ≤ 22
⇒ 14-11 ≤ 3x and 3x ≤ 22-11
⇒ 3 ≤ 3x and 3x ≤ 11
⇒ 1 ≤ x and x ≤ 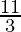
⇒ 1 ≤ x ≤ 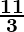
Hence, all real numbers x greater than or equal to 1 but less than or equal to 11/3 are solution of given 7 ≤ 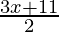 ≤ 11 equality.
≤ 11 equality.
x ∈ [1, 11/3]
Solve the inequalities in Exercises 7 to 10 and represent the solution graphically on number line.
Question 7. 5x + 1 > – 24, 5x – 1 < 24
Solution:
So, from given data
5x + 1 > – 24 ……………………(1)
5x – 1 < 24 …………………….(2)
From inequality (1), we have
5x + 1 > – 24
5x > – 24-1
x > – 25/5
x > -5 ………………………….(3)
Also, from inequality (2), we have
5x – 1 < 24
5x < 24+1
x < 25/5
x < 5 ……………………………(4)
So, from (3) and (4), we can conclude that,
-5 < x < 5 ……………….(5)
If we draw the graph of inequalities (5) on the number line, we see that the values of x, which are common to both, are
x ∈ (-5,5)

Thus, solution of the system are real numbers x lying between -5 and 5 excluding -5 and 5.
Question 8. 2 (x – 1) < x + 5, 3 (x + 2) > 2 – x
Solution:
So, from given data
2 (x – 1) < x + 5 ……………………(1)
3 (x + 2) > 2 – x …………………….(2)
From inequality (1), we have
2 (x – 1) < x + 5
2x – 2 < x + 5
2x – x < 5+2
x < 7 ………………………….(3)
Also, from inequality (2), we have
3 (x + 2) > 2 – x
3x + 6 > 2 – x
3x + x > 2 – 6
4x > -4
x > -1 ……………………………(4)
So, from (3) and (4), we can conclude that,
-1 < x < 7 ……………….(5)
If we draw the graph of inequalities (5) on the number line, we see that the values of x, which are common to both, are
x ∈ (-1,7)

Thus, solution of the system are real numbers x lying between -1 and 7 excluding -1 and 7.
Question 9. 3x – 7 > 2 (x – 6) , 6 – x > 11 – 2x
Solution:
So, from given data
3x – 7 > 2 (x – 6) ……………………(1)
6 – x > 11 – 2x …………………….(2)
From inequality (1), we have
3x – 7 > 2 (x – 6)
3x – 7 > 2x – 12
3x – 2x > – 12+7
x > -5 ………………………….(3)
Also, from inequality (2), we have
6 – x > 11 – 2x
– x+2x > 11 -6
x > 5 ……………………………(4)
So, from (3) and (4), we can conclude that,
5 < x ……………….(5)
If we draw the graph of inequalities (5) on the number line, we see that the values of x, which are common to both, are
x ∈ (5,∞)

Thus, solution of the system are real numbers x lying between 5 and ∞ excluding 5 .
Question 10. 5 (2x – 7) – 3 (2x + 3) ≤ 0 , 2x + 19 ≤ 6x + 47
Solution:
So, from given data
5 (2x – 7) – 3 (2x + 3) ≤ 0 ……………………(1)
2x + 19 ≤ 6x + 47 …………………….(2)
From inequality (1), we have
5 (2x – 7) – 3 (2x + 3) ≤ 0
10x – 35 -6x – 9 ≤ 0
4x – 44 ≤ 0
4x ≤ 44
x ≤ 44/4
x ≤ 11 ………………………….(3)
Also, from inequality (2), we have
2x + 19 ≤ 6x + 47
2x – 6x ≤ 47 – 19
-4x ≤ 28
4x ≥ -28 [multiplying the inequality with (-1) which changes the inequality sign]
x ≥ -28/4
x ≥ -7 ……………………………(4)
So, from (3) and (4), we can conclude that,
-7 ≤ x ≤ 11 ……………….(5)
If we draw the graph of inequalities (5) on the number line, we see that the values of x, which are common to both, are
x ∈ [-7,11)

Thus, solution of the system are real numbers x lying between -7 and 11 including -7 and 11 .
Question 11. A solution is to be kept between 68° F and 77° F. What is the range in temperature in degree Celsius (C) if the Celsius / Fahrenheit (F) conversion formula is given by F = (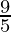 )C + 32
)C + 32
Solution:
According to the given data
The solution has to be kept between 68° F and 77° F
So, we have,
68° < F < 77°
Substituting, F = 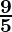 C + 32
C + 32
⇒ 68° < 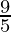 C + 32 < 77°
C + 32 < 77°
⇒ 68°- 32° < 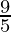 C < 77°- 32°
C < 77°- 32°
⇒ 36° < 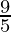 C < 45°
C < 45°
⇒ 36×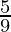 < C < 45×
< C < 45×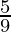
⇒ 20° < C < 25°
Hence, here we get,
The range of temperature in degree Celsius is between 20° C to 25° C.
Question 12. A solution of 8% boric acid is to be diluted by adding a 2% boric acid solution to it. The resulting mixture is to be more than 4% but less than 6% boric acid. If we have 640 litres of the 8% solution, how many litres of the 2% solution will have to be added?
Solution:
According to the given data,
Here, 8% of solution of boric acid = 640 litres
So, we can take the amount of 2% boric acid solution added as x litres
Hence, Total mixture = (x + 640) litres
As it is given,
The resulting mixture has to be more than 4% but less than 6% boric acid
⇒ (2% of x + 8% of 640) > (4% of (x + 640)) and (2% of x + 8% of 640) < (6% of (x + 640))
⇒ (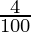 ) × (x + 640) < (
) × (x + 640) < (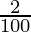 ) × x + (
) × x + (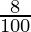 ) × 640) < (
) × 640) < (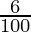 ) × (x + 640)
) × (x + 640)
⇒ 4(x + 640) < (2×x + 8× 640) < 6(x + 640)
⇒ 4x + 2560 < 2x +5120 < 6x+3840
In this case, we have two inequalities,
⇒ 4x + 2560 < 2x +5120 and 2x +5120 < 6x+3840
⇒ 4x – 2x < 5120 – 2560 and 5120-3840 < 6x-2x
⇒ 2x < 2560 and 1280 < 4x
⇒ x < 2560/2 and 1280/4 < x
⇒ x < 1280 and 320 < x
⇒ 320 < x < 1280
Therefore, the number of litres of 2% of boric acid solution that has to be added will be more than 320 litres but less than 1280 litres.
Question 13. How many litres of water will have to be added to 1125 litres of the 45% solution of acid so that the resulting mixture will contain more than 25% but less than 30% acid content?
Solution:
According to the given data,
Here, 45% of solution of acid = 1125 litres
Let the amount of water added in the solution = x litres
Resulting mixture = (x + 1125) litres
As it is given,
The resulting mixture has to be more than 25% but less than 30% acid content
Amount of acid in resulting mixture = 45% of 1125 litres.
⇒ 45% of 1125 < 30% of (x + 1125) and 45% of 1125 > 25% of (x + 1125)
⇒ 25% of (x + 1125) < 45% of 1125 < 30% of (x + 1125)
In this case, we have two inequalities,
⇒ (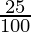 × (x + 1125)) < (
× (x + 1125)) < (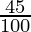 × 1125) and (
× 1125) and (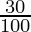 × (x + 1125)) > (
× (x + 1125)) > (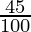 × 1125)
× 1125)
⇒ (25(x + 1125)) < (45×1125) and (30(x + 1125)) > (45×1125)
⇒ (x + 1125) < (45×1125)/25 and (x + 1125) > (45×1125)/30
⇒ (x + 1125) < 2025 and (x + 1125) > 3375/2
⇒ 3375/2 < (x + 1125) < 2025
⇒ (3375/2)-1125 < x < 2025-1125
⇒ 1125/2 < x < 900
⇒ 562.5 < x < 900
Therefore, the number of litres of water that has to be added will have to be more than 562.5 litres but less than 900 litres.
Question 14. IQ of a person is given by the formula, IQ = ( ) × 100, where MA is mental age and CA is chronological age. If 80 ≤ IQ ≤ 140 for a group of 12 years old children, find the range of their mental age.
) × 100, where MA is mental age and CA is chronological age. If 80 ≤ IQ ≤ 140 for a group of 12 years old children, find the range of their mental age.
Solution:
According to the given data, we have
Chronological age = CA = 12 years
IQ for age group of 12 is in the range,
80 ≤ IQ ≤ 140
Substituting, IQ = (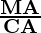 ) × 100
) × 100
⇒ 80 ≤  × 100 ≤ 140
× 100 ≤ 140
⇒ 80 ≤ 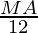 × 100 ≤ 140
× 100 ≤ 140
⇒ 80×12/100 ≤ MA ≤ 140×12/100
⇒ 96/10 ≤ MA ≤ 168/10
⇒ 9.6 ≤ MA ≤ 16.8
Hence, Range of mental age (MA) of the group of 12 years old children is 9.6 ≤ MA ≤ 16.8
Share your thoughts in the comments
Please Login to comment...