Detecting negative cycle using Floyd Warshall
Last Updated :
13 Oct, 2023
We are given a directed graph. We need compute whether the graph has negative cycle or not. A negative cycle is one in which the overall sum of the cycle comes negative.
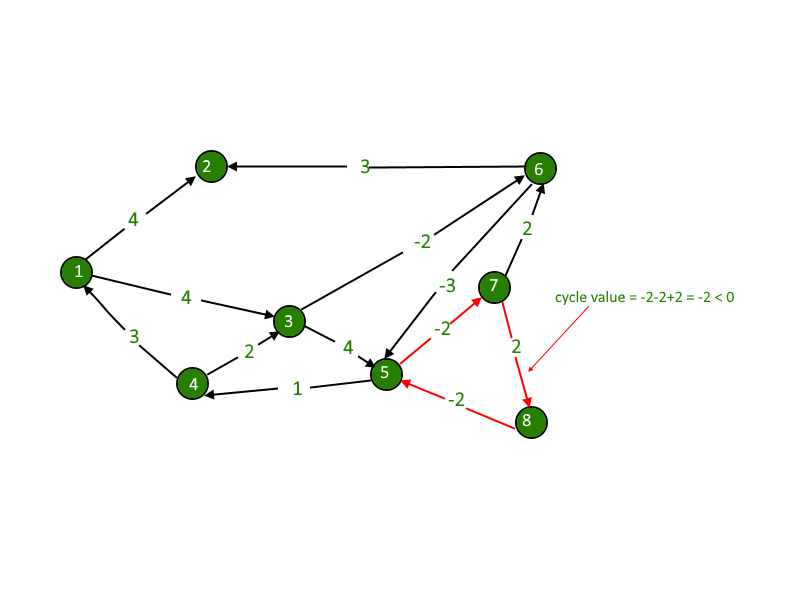
Negative weights are found in various applications of graphs. For example, instead of paying cost for a path, we may get some advantage if we follow the path.
Examples:
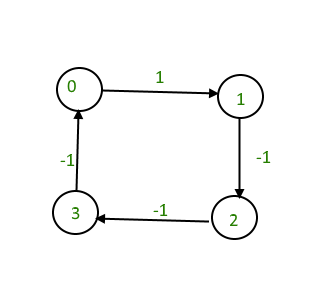
Input : 4 4
0 1 1
1 2 -1
2 3 -1
3 0 -1
Output : Yes
The graph contains a negative cycle.
We have discussed Bellman Ford Algorithm based solution for this problem.
In this post, Floyd Warshall Algorithm based solution is discussed that works for both connected and disconnected graphs.
Distance of any node from itself is always zero. But in some cases, as in this example, when we traverse further from 4 to 1, the distance comes out to be -2, i.e. distance of 1 from 1 will become -2. This is our catch, we just have to check the nodes distance from itself and if it comes out to be negative, we will detect the required negative cycle.
Implementation:
C++
#include<bits/stdc++.h>
using namespace std;
#define V 4
#define INF 99999
void printSolution(int dist[][V]);
bool negCyclefloydWarshall(int graph[][V])
{
int dist[V][V], i, j, k;
for (i = 0; i < V; i++)
for (j = 0; j < V; j++)
dist[i][j] = graph[i][j];
for (k = 0; k < V; k++)
{
for (i = 0; i < V; i++)
{
for (j = 0; j < V; j++)
{
if (dist[i][k] + dist[k][j] < dist[i][j])
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
for (int i = 0; i < V; i++)
if (dist[i][i] < 0)
return true;
return false;
}
int main()
{
int graph[V][V] = { {0 , 1 , INF , INF},
{INF , 0 , -1 , INF},
{INF , INF , 0 , -1},
{-1 , INF , INF , 0}};
if (negCyclefloydWarshall(graph))
cout << "Yes";
else
cout << "No";
return 0;
}
|
Java
class GFG
{
static final int V = 4;
static final int INF = 99999;
static boolean negCyclefloydWarshall(int graph[][])
{
int dist[][] = new int[V][V], i, j, k;
for (i = 0; i < V; i++)
for (j = 0; j < V; j++)
dist[i][j] = graph[i][j];
for (k = 0; k < V; k++)
{
for (i = 0; i < V; i++)
{
for (j = 0; j < V; j++)
{
if (dist[i][k] + dist[k][j] < dist[i][j])
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
for (i = 0; i < V; i++)
if (dist[i][i] < 0)
return true;
return false;
}
public static void main (String[] args)
{
int graph[][] = { {0, 1, INF, INF},
{INF, 0, -1, INF},
{INF, INF, 0, -1},
{-1, INF, INF, 0}};
if (negCyclefloydWarshall(graph))
System.out.print("Yes");
else
System.out.print("No");
}
}
|
Python3
V = 4
INF = 99999
def negCyclefloydWarshall(graph):
dist=[[0 for i in range(V+1)]for j in range(V+1)]
for i in range(V):
for j in range(V):
dist[i][j] = graph[i][j]
for k in range(V):
for i in range(V):
for j in range(V):
if (dist[i][k] + dist[k][j] < dist[i][j]):
dist[i][j] = dist[i][k] + dist[k][j]
for i in range(V):
if (dist[i][i] < 0):
return True
return False
graph = [ [0, 1, INF, INF],
[INF, 0, -1, INF],
[INF, INF, 0, -1],
[-1, INF, INF, 0]]
if (negCyclefloydWarshall(graph)):
print("Yes")
else:
print("No")
|
C#
using System;
namespace Cycle
{
public class GFG
{
static int V = 4;
static int INF = 99999;
static bool negCyclefloydWarshall(int [,]graph)
{
int [,]dist = new int[V,V];
int i, j, k;
for (i = 0; i < V; i++)
for (j = 0; j < V; j++)
dist[i,j] = graph[i,j];
for (k = 0; k < V; k++)
{
for (i = 0; i < V; i++)
{
for (j = 0; j < V; j++)
{
if (dist[i,k] + dist[k,j] < dist[i,j])
dist[i,j] = dist[i,k] + dist[k,j];
}
}
}
for (i = 0; i < V; i++)
if (dist[i,i] < 0)
return true;
return false;
}
public static void Main()
{
int [,]graph = { {0, 1, INF, INF},
{INF, 0, -1, INF},
{INF, INF, 0, -1},
{-1, INF, INF, 0}};
if (negCyclefloydWarshall(graph))
Console.Write("Yes");
else
Console.Write("No");
}
}
}
|
Javascript
<script>
var V = 4;
var INF = 99999;
function negCyclefloydWarshall(graph)
{
var dist = Array.from(Array(V), ()=>Array(V));
var i, j, k;
for (i = 0; i < V; i++)
for (j = 0; j < V; j++)
dist[i][j] = graph[i][j];
for (k = 0; k < V; k++)
{
for (i = 0; i < V; i++)
{
for (j = 0; j < V; j++)
{
if (dist[i][k] + dist[k][j] < dist[i][j])
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
for (i = 0; i < V; i++)
if (dist[i][i] < 0)
return true;
return false;
}
var graph = [ [0, 1, INF, INF],
[INF, 0, -1, INF],
[INF, INF, 0, -1],
[-1, INF, INF, 0]];
if (negCyclefloydWarshall(graph))
document.write("Yes");
else
document.write("No");
</script>
|
The time complexity of the Floyd Warshall algorithm is O(V^3) where V is the number of vertices in the graph. This is because the algorithm uses a nested loop structure, where the outermost loop runs V times, the middle loop runs V times and the innermost loop also runs V times. Therefore, the total number of iterations is V * V * V which results in O(V^3) time complexity.
The space complexity of the Floyd Warshall algorithm is O(V^2) where V is the number of vertices in the graph. This is because the algorithm uses a 2D array of size V x V to store the shortest distances between every pair of vertices. Therefore, the total space required is V * V which results in O(V^2) space complexity.
Share your thoughts in the comments
Please Login to comment...