Floyd Warshall Algorithm
Last Updated :
04 Apr, 2024
The Floyd-Warshall algorithm, named after its creators Robert Floyd and Stephen Warshall, is a fundamental algorithm in computer science and graph theory. It is used to find the shortest paths between all pairs of nodes in a weighted graph. This algorithm is highly efficient and can handle graphs with both positive and negative edge weights, making it a versatile tool for solving a wide range of network and connectivity problems.

Floyd Warshall Algorithm:
The Floyd Warshall Algorithm is an all pair shortest path algorithm unlike Dijkstra and Bellman Ford which are single source shortest path algorithms. This algorithm works for both the directed and undirected weighted graphs. But, it does not work for the graphs with negative cycles (where the sum of the edges in a cycle is negative). It follows Dynamic Programming approach to check every possible path going via every possible node in order to calculate shortest distance between every pair of nodes.
Idea Behind Floyd Warshall Algorithm:
Suppose we have a graph G[][] with V vertices from 1 to N. Now we have to evaluate a shortestPathMatrix[][] where shortestPathMatrix[i][j] represents the shortest path between vertices i and j.
Obviously the shortest path between i to j will have some k number of intermediate nodes. The idea behind floyd warshall algorithm is to treat each and every vertex from 1 to N as an intermediate node one by one.
The following figure shows the above optimal substructure property in floyd warshall algorithm:

Floyd Warshall Algorithm Algorithm:
- Initialize the solution matrix same as the input graph matrix as a first step.
- Then update the solution matrix by considering all vertices as an intermediate vertex.
- The idea is to pick all vertices one by one and updates all shortest paths which include the picked vertex as an intermediate vertex in the shortest path.
- When we pick vertex number k as an intermediate vertex, we already have considered vertices {0, 1, 2, .. k-1} as intermediate vertices.
- For every pair (i, j) of the source and destination vertices respectively, there are two possible cases.
- k is not an intermediate vertex in shortest path from i to j. We keep the value of dist[i][j] as it is.
- k is an intermediate vertex in shortest path from i to j. We update the value of dist[i][j] as dist[i][k] + dist[k][j], if dist[i][j] > dist[i][k] + dist[k][j]
Pseudo-Code of Floyd Warshall Algorithm :
For k = 0 to n – 1
For i = 0 to n – 1
For j = 0 to n – 1
Distance[i, j] = min(Distance[i, j], Distance[i, k] + Distance[k, j])
where i = source Node, j = Destination Node, k = Intermediate Node
Illustration of Floyd Warshall Algorithm :
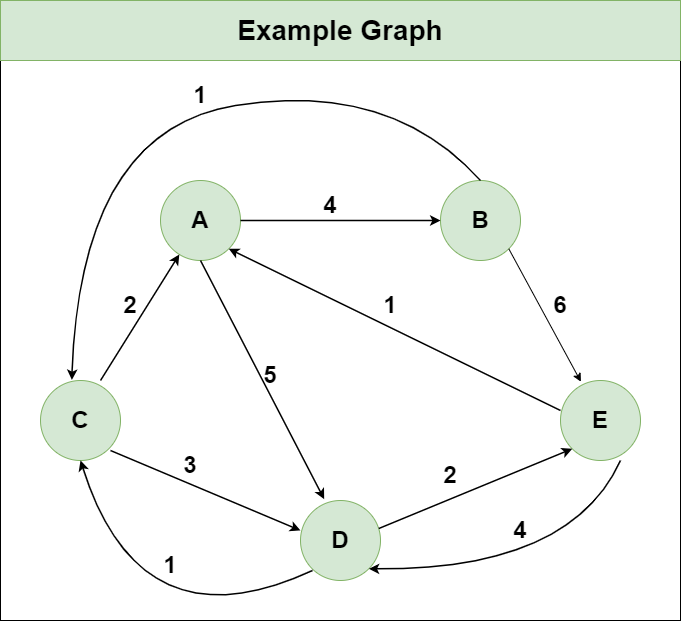
Suppose we have a graph as shown in the image:
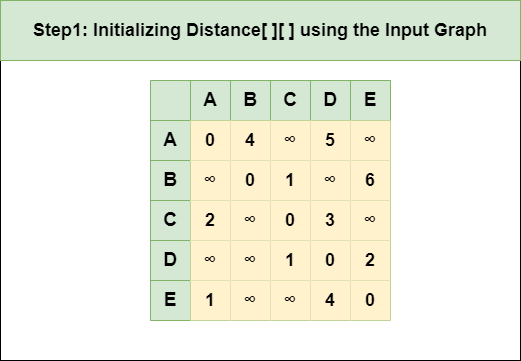
Step 1: Initialize the Distance[][] matrix using the input graph such that Distance[i][j]= weight of edge from i to j, also Distance[i][j] = Infinity if there is no edge from i to j.
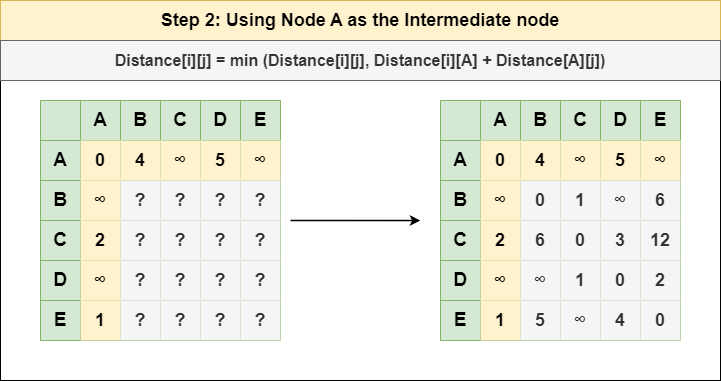
Step 2: Treat node A as an intermediate node and calculate the Distance[][] for every {i,j} node pair using the formula:
= Distance[i][j] = minimum (Distance[i][j], (Distance from i to A) + (Distance from A to j ))
= Distance[i][j] = minimum (Distance[i][j], Distance[i][A] + Distance[A][j])
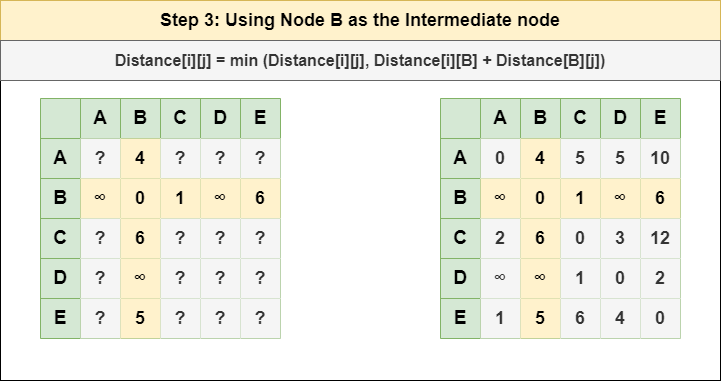
Step 3: Treat node B as an intermediate node and calculate the Distance[][] for every {i,j} node pair using the formula:
= Distance[i][j] = minimum (Distance[i][j], (Distance from i to B) + (Distance from B to j ))
= Distance[i][j] = minimum (Distance[i][j], Distance[i][B] + Distance[B][j])
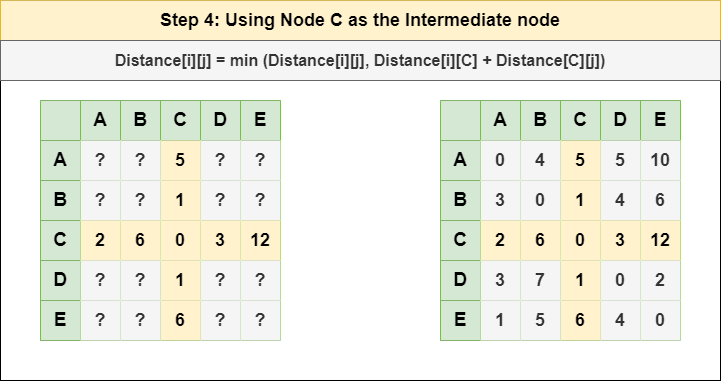
Step 4: Treat node C as an intermediate node and calculate the Distance[][] for every {i,j} node pair using the formula:
= Distance[i][j] = minimum (Distance[i][j], (Distance from i to C) + (Distance from C to j ))
= Distance[i][j] = minimum (Distance[i][j], Distance[i][C] + Distance[C][j])
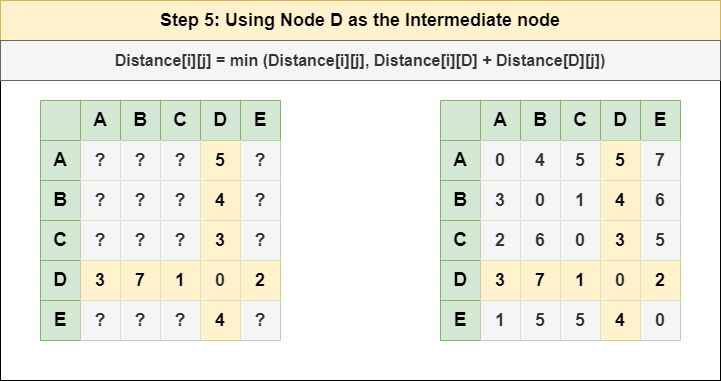
Step 5: Treat node D as an intermediate node and calculate the Distance[][] for every {i,j} node pair using the formula:
= Distance[i][j] = minimum (Distance[i][j], (Distance from i to D) + (Distance from D to j ))
= Distance[i][j] = minimum (Distance[i][j], Distance[i][D] + Distance[D][j])
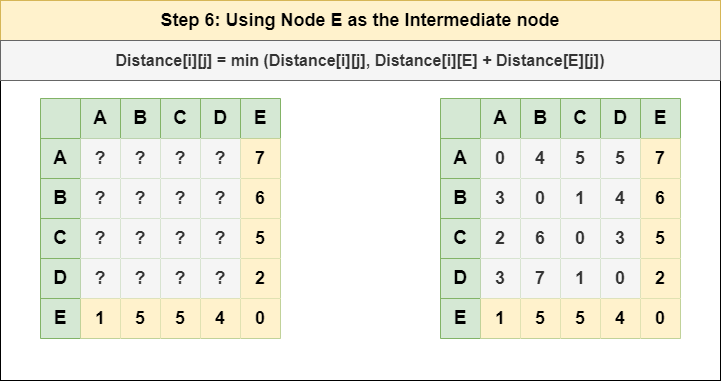
Step 6: Treat node E as an intermediate node and calculate the Distance[][] for every {i,j} node pair using the formula:
= Distance[i][j] = minimum (Distance[i][j], (Distance from i to E) + (Distance from E to j ))
= Distance[i][j] = minimum (Distance[i][j], Distance[i][E] + Distance[E][j])
Step 7: Since all the nodes have been treated as an intermediate node, we can now return the updated Distance[][] matrix as our answer matrix.

Below is the implementation of the above approach:
C++
// C++ Program for Floyd Warshall Algorithm
#include <bits/stdc++.h>
using namespace std;
// Number of vertices in the graph
#define V 4
/* Define Infinite as a large enough
value.This value will be used for
vertices not connected to each other */
#define INF 99999
// A function to print the solution matrix
void printSolution(int dist[][V]);
// Solves the all-pairs shortest path
// problem using Floyd Warshall algorithm
void floydWarshall(int dist[][V])
{
int i, j, k;
/* Add all vertices one by one to
the set of intermediate vertices.
---> Before start of an iteration,
we have shortest distances between all
pairs of vertices such that the
shortest distances consider only the
vertices in set {0, 1, 2, .. k-1} as
intermediate vertices.
----> After the end of an iteration,
vertex no. k is added to the set of
intermediate vertices and the set becomes {0, 1, 2, ..
k} */
for (k = 0; k < V; k++) {
// Pick all vertices as source one by one
for (i = 0; i < V; i++) {
// Pick all vertices as destination for the
// above picked source
for (j = 0; j < V; j++) {
// If vertex k is on the shortest path from
// i to j, then update the value of
// dist[i][j]
if (dist[i][j] > (dist[i][k] + dist[k][j])
&& (dist[k][j] != INF
&& dist[i][k] != INF))
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
// Print the shortest distance matrix
printSolution(dist);
}
/* A utility function to print solution */
void printSolution(int dist[][V])
{
cout << "The following matrix shows the shortest "
"distances"
" between every pair of vertices \n";
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
if (dist[i][j] == INF)
cout << "INF"
<< " ";
else
cout << dist[i][j] << " ";
}
cout << endl;
}
}
// Driver's code
int main()
{
/* Let us create the following weighted graph
10
(0)------->(3)
| /|\
5 | |
| | 1
\|/ |
(1)------->(2)
3 */
int graph[V][V] = { { 0, 5, INF, 10 },
{ INF, 0, 3, INF },
{ INF, INF, 0, 1 },
{ INF, INF, INF, 0 } };
// Function call
floydWarshall(graph);
return 0;
}
// This code is contributed by Mythri J L
// C Program for Floyd Warshall Algorithm
#include <stdio.h>
// Number of vertices in the graph
#define V 4
/* Define Infinite as a large enough
value. This value will be used
for vertices not connected to each other */
#define INF 99999
// A function to print the solution matrix
void printSolution(int dist[][V]);
// Solves the all-pairs shortest path
// problem using Floyd Warshall algorithm
void floydWarshall(int dist[][V])
{
int i, j, k;
/* Add all vertices one by one to
the set of intermediate vertices.
---> Before start of an iteration, we
have shortest distances between all
pairs of vertices such that the shortest
distances consider only the
vertices in set {0, 1, 2, .. k-1} as
intermediate vertices.
----> After the end of an iteration,
vertex no. k is added to the set of
intermediate vertices and the set
becomes {0, 1, 2, .. k} */
for (k = 0; k < V; k++) {
// Pick all vertices as source one by one
for (i = 0; i < V; i++) {
// Pick all vertices as destination for the
// above picked source
for (j = 0; j < V; j++) {
// If vertex k is on the shortest path from
// i to j, then update the value of
// dist[i][j]
if (dist[i][k] + dist[k][j] < dist[i][j])
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
// Print the shortest distance matrix
printSolution(dist);
}
/* A utility function to print solution */
void printSolution(int dist[][V])
{
printf(
"The following matrix shows the shortest distances"
" between every pair of vertices \n");
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
if (dist[i][j] == INF)
printf("%7s", "INF");
else
printf("%7d", dist[i][j]);
}
printf("\n");
}
}
// driver's code
int main()
{
/* Let us create the following weighted graph
10
(0)------->(3)
| /|\
5 | |
| | 1
\|/ |
(1)------->(2)
3 */
int graph[V][V] = { { 0, 5, INF, 10 },
{ INF, 0, 3, INF },
{ INF, INF, 0, 1 },
{ INF, INF, INF, 0 } };
// Function call
floydWarshall(graph);
return 0;
}
// Java program for Floyd Warshall All Pairs Shortest
// Path algorithm.
import java.io.*;
import java.lang.*;
import java.util.*;
class AllPairShortestPath {
final static int INF = 99999, V = 4;
void floydWarshall(int dist[][])
{
int i, j, k;
/* Add all vertices one by one
to the set of intermediate
vertices.
---> Before start of an iteration,
we have shortest
distances between all pairs
of vertices such that
the shortest distances consider
only the vertices in
set {0, 1, 2, .. k-1} as
intermediate vertices.
----> After the end of an iteration,
vertex no. k is added
to the set of intermediate
vertices and the set
becomes {0, 1, 2, .. k} */
for (k = 0; k < V; k++) {
// Pick all vertices as source one by one
for (i = 0; i < V; i++) {
// Pick all vertices as destination for the
// above picked source
for (j = 0; j < V; j++) {
// If vertex k is on the shortest path
// from i to j, then update the value of
// dist[i][j]
if (dist[i][k] + dist[k][j]
< dist[i][j])
dist[i][j]
= dist[i][k] + dist[k][j];
}
}
}
// Print the shortest distance matrix
printSolution(dist);
}
void printSolution(int dist[][])
{
System.out.println(
"The following matrix shows the shortest "
+ "distances between every pair of vertices");
for (int i = 0; i < V; ++i) {
for (int j = 0; j < V; ++j) {
if (dist[i][j] == INF)
System.out.print("INF ");
else
System.out.print(dist[i][j] + " ");
}
System.out.println();
}
}
// Driver's code
public static void main(String[] args)
{
/* Let us create the following weighted graph
10
(0)------->(3)
| /|\
5 | |
| | 1
\|/ |
(1)------->(2)
3 */
int graph[][] = { { 0, 5, INF, 10 },
{ INF, 0, 3, INF },
{ INF, INF, 0, 1 },
{ INF, INF, INF, 0 } };
AllPairShortestPath a = new AllPairShortestPath();
// Function call
a.floydWarshall(graph);
}
}
// Contributed by Aakash Hasija
# Python3 Program for Floyd Warshall Algorithm
# Number of vertices in the graph
V = 4
# Define infinity as the large
# enough value. This value will be
# used for vertices not connected to each other
INF = 99999
# Solves all pair shortest path
# via Floyd Warshall Algorithm
def floydWarshall(graph):
""" dist[][] will be the output
matrix that will finally
have the shortest distances
between every pair of vertices """
""" initializing the solution matrix
same as input graph matrix
OR we can say that the initial
values of shortest distances
are based on shortest paths considering no
intermediate vertices """
dist = list(map(lambda i: list(map(lambda j: j, i)), graph))
""" Add all vertices one by one
to the set of intermediate
vertices.
---> Before start of an iteration,
we have shortest distances
between all pairs of vertices
such that the shortest
distances consider only the
vertices in the set
{0, 1, 2, .. k-1} as intermediate vertices.
----> After the end of a
iteration, vertex no. k is
added to the set of intermediate
vertices and the
set becomes {0, 1, 2, .. k}
"""
for k in range(V):
# pick all vertices as source one by one
for i in range(V):
# Pick all vertices as destination for the
# above picked source
for j in range(V):
# If vertex k is on the shortest path from
# i to j, then update the value of dist[i][j]
dist[i][j] = min(dist[i][j],
dist[i][k] + dist[k][j]
)
printSolution(dist)
# A utility function to print the solution
def printSolution(dist):
print("Following matrix shows the shortest distances\
between every pair of vertices")
for i in range(V):
for j in range(V):
if(dist[i][j] == INF):
print("%7s" % ("INF"), end=" ")
else:
print("%7d\t" % (dist[i][j]), end=' ')
if j == V-1:
print()
# Driver's code
if __name__ == "__main__":
"""
10
(0)------->(3)
| /|\
5 | |
| | 1
\|/ |
(1)------->(2)
3 """
graph = [[0, 5, INF, 10],
[INF, 0, 3, INF],
[INF, INF, 0, 1],
[INF, INF, INF, 0]
]
# Function call
floydWarshall(graph)
# This code is contributed by Mythri J L
// C# program for Floyd Warshall All
// Pairs Shortest Path algorithm.
using System;
public class AllPairShortestPath {
readonly static int INF = 99999, V = 4;
void floydWarshall(int[, ] graph)
{
int[, ] dist = new int[V, V];
int i, j, k;
// Initialize the solution matrix
// same as input graph matrix
// Or we can say the initial
// values of shortest distances
// are based on shortest paths
// considering no intermediate
// vertex
for (i = 0; i < V; i++) {
for (j = 0; j < V; j++) {
dist[i, j] = graph[i, j];
}
}
/* Add all vertices one by one to
the set of intermediate vertices.
---> Before start of a iteration,
we have shortest distances
between all pairs of vertices
such that the shortest distances
consider only the vertices in
set {0, 1, 2, .. k-1} as
intermediate vertices.
---> After the end of a iteration,
vertex no. k is added
to the set of intermediate
vertices and the set
becomes {0, 1, 2, .. k} */
for (k = 0; k < V; k++) {
// Pick all vertices as source
// one by one
for (i = 0; i < V; i++) {
// Pick all vertices as destination
// for the above picked source
for (j = 0; j < V; j++) {
// If vertex k is on the shortest
// path from i to j, then update
// the value of dist[i][j]
if (dist[i, k] + dist[k, j]
< dist[i, j]) {
dist[i, j]
= dist[i, k] + dist[k, j];
}
}
}
}
// Print the shortest distance matrix
printSolution(dist);
}
void printSolution(int[, ] dist)
{
Console.WriteLine(
"Following matrix shows the shortest "
+ "distances between every pair of vertices");
for (int i = 0; i < V; ++i) {
for (int j = 0; j < V; ++j) {
if (dist[i, j] == INF) {
Console.Write("INF ");
}
else {
Console.Write(dist[i, j] + " ");
}
}
Console.WriteLine();
}
}
// Driver's Code
public static void Main(string[] args)
{
/* Let us create the following
weighted graph
10
(0)------->(3)
| /|\
5 | |
| | 1
\|/ |
(1)------->(2)
3 */
int[, ] graph = { { 0, 5, INF, 10 },
{ INF, 0, 3, INF },
{ INF, INF, 0, 1 },
{ INF, INF, INF, 0 } };
AllPairShortestPath a = new AllPairShortestPath();
// Function call
a.floydWarshall(graph);
}
}
// This article is contributed by
// Abdul Mateen Mohammed
// A JavaScript program for Floyd Warshall All
// Pairs Shortest Path algorithm.
var INF = 99999;
class AllPairShortestPath {
constructor() {
this.V = 4;
}
floydWarshall(graph) {
var dist = Array.from(Array(this.V), () => new Array(this.V).fill(0));
var i, j, k;
// Initialize the solution matrix
// same as input graph matrix
// Or we can say the initial
// values of shortest distances
// are based on shortest paths
// considering no intermediate
// vertex
for (i = 0; i < this.V; i++) {
for (j = 0; j < this.V; j++) {
dist[i][j] = graph[i][j];
}
}
/* Add all vertices one by one to
the set of intermediate vertices.
---> Before start of a iteration,
we have shortest distances
between all pairs of vertices
such that the shortest distances
consider only the vertices in
set {0, 1, 2, .. k-1} as
intermediate vertices.
---> After the end of a iteration,
vertex no. k is added
to the set of intermediate
vertices and the set
becomes {0, 1, 2, .. k} */
for (k = 0; k < this.V; k++) {
// Pick all vertices as source
// one by one
for (i = 0; i < this.V; i++) {
// Pick all vertices as destination
// for the above picked source
for (j = 0; j < this.V; j++) {
// If vertex k is on the shortest
// path from i to j, then update
// the value of dist[i][j]
if (dist[i][k] + dist[k][j] < dist[i][j]) {
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
}
// Print the shortest distance matrix
this.printSolution(dist);
}
printSolution(dist) {
document.write(
"Following matrix shows the shortest " +
"distances between every pair of vertices<br>"
);
for (var i = 0; i < this.V; ++i) {
for (var j = 0; j < this.V; ++j) {
if (dist[i][j] == INF) {
document.write(" INF ");
} else {
document.write("  " + dist[i][j] + " ");
}
}
document.write("<br>");
}
}
}
// Driver Code
/* Let us create the following
weighted graph
10
(0)------->(3)
| /|\
5 | |
| | 1
\|/ |
(1)------->(2)
3 */
var graph = [
[0, 5, INF, 10],
[INF, 0, 3, INF],
[INF, INF, 0, 1],
[INF, INF, INF, 0],
];
var a = new AllPairShortestPath();
// Print the solution
a.floydWarshall(graph);
// This code is contributed by rdtaank.
<?php
// PHP Program for Floyd Warshall Algorithm
// Solves the all-pairs shortest path problem
// using Floyd Warshall algorithm
function floydWarshall ($graph, $V, $INF)
{
/* dist[][] will be the output matrix
that will finally have the shortest
distances between every pair of vertices */
$dist = array(array(0,0,0,0),
array(0,0,0,0),
array(0,0,0,0),
array(0,0,0,0));
/* Initialize the solution matrix same
as input graph matrix. Or we can say the
initial values of shortest distances are
based on shortest paths considering no
intermediate vertex. */
for ($i = 0; $i < $V; $i++)
for ($j = 0; $j < $V; $j++)
$dist[$i][$j] = $graph[$i][$j];
/* Add all vertices one by one to the set
of intermediate vertices.
---> Before start of an iteration, we have
shortest distances between all pairs of
vertices such that the shortest distances
consider only the vertices in set
{0, 1, 2, .. k-1} as intermediate vertices.
----> After the end of an iteration, vertex
no. k is added to the set of intermediate
vertices and the set becomes {0, 1, 2, .. k} */
for ($k = 0; $k < $V; $k++)
{
// Pick all vertices as source one by one
for ($i = 0; $i < $V; $i++)
{
// Pick all vertices as destination
// for the above picked source
for ($j = 0; $j < $V; $j++)
{
// If vertex k is on the shortest path from
// i to j, then update the value of dist[i][j]
if ($dist[$i][$k] + $dist[$k][$j] <
$dist[$i][$j])
$dist[$i][$j] = $dist[$i][$k] +
$dist[$k][$j];
}
}
}
// Print the shortest distance matrix
printSolution($dist, $V, $INF);
}
/* A utility function to print solution */
function printSolution($dist, $V, $INF)
{
echo "The following matrix shows the " .
"shortest distances between " .
"every pair of vertices \n";
for ($i = 0; $i < $V; $i++)
{
for ($j = 0; $j < $V; $j++)
{
if ($dist[$i][$j] == $INF)
echo "INF " ;
else
echo $dist[$i][$j], " ";
}
echo "\n";
}
}
// Drivers' Code
// Number of vertices in the graph
$V = 4 ;
/* Define Infinite as a large enough
value. This value will be used for
vertices not connected to each other */
$INF = 99999 ;
/* Let us create the following weighted graph
10
(0)------->(3)
| /|\
5 | |
| | 1
\|/ |
(1)------->(2)
3 */
$graph = array(array(0, 5, $INF, 10),
array($INF, 0, 3, $INF),
array($INF, $INF, 0, 1),
array($INF, $INF, $INF, 0));
// Function call
floydWarshall($graph, $V, $INF);
// This code is contributed by Ryuga
?>
OutputThe following matrix shows the shortest distances between every pair of vertices
0 5 8 9
INF 0 3 4
INF INF 0 1
INF INF INF 0
- Time Complexity: O(V3), where V is the number of vertices in the graph and we run three nested loops each of size V
- Auxiliary Space: O(V2), to create a 2-D matrix in order to store the shortest distance for each pair of nodes.
Note: The above program only prints the shortest distances. We can modify the solution to print the shortest paths also by storing the predecessor information in a separate 2D matrix.
Why Floyd-Warshall Algorithm better for Dense Graphs and not for Sparse Graphs?
Dense Graph: A graph in which the number of edges are significantly much higher than the number of vertices.
Sparse Graph: A graph in which the number of edges are very much low.
No matter how many edges are there in the graph the Floyd Warshall Algorithm runs for O(V3) times therefore it is best suited for Dense graphs. In the case of sparse graphs, Johnson’s Algorithm is more suitable.
Real World Applications of Floyd-Warshall Algorithm:
- In computer networking, the algorithm can be used to find the shortest path between all pairs of nodes in a network. This is termed as network routing.
- Flight Connectivity In the aviation industry to find the shortest path between the airports.
- GIS(Geographic Information Systems) applications often involve analyzing spatial data, such as road networks, to find the shortest paths between locations.
- Kleene’s algorithm which is a generalization of floyd warshall, can be used to find regular expression for a regular language.
Share your thoughts in the comments
Please Login to comment...