Detect cycle in an undirected graph

Given an undirected graph, how to check if there is a cycle in the graph? 

Example,

Click here for the Complete Course!

Input: n = 4, e = 4 

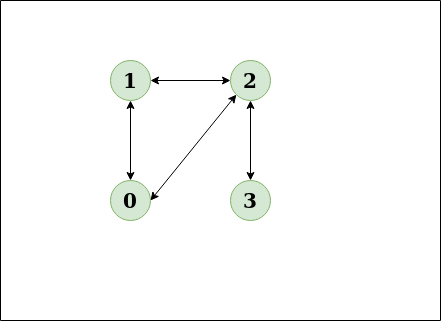
Output: Yes 

Explanation:  0 1, 1 2, 2 3, 0 2 

Diagram: 

The diagram clearly shows a cycle 0 to 2 to 1 to 0

Input: n = 4, e = 3 , 0 1, 1 2, 2 3 

Output: No 

Explanation:

Diagram: 

The diagram clearly shows no cycle 

Articles about cycle detection:

• cycle detection for directed graph.
• union-find algorithm for cycle detection in undirected graphs.

Approach: Run a DFS from every unvisited node. Depth First Traversal can be used to detect a cycle in a Graph. DFS for a connected graph produces a tree. There is a cycle in a graph only if there is a back edge present in the graph. A back edge is an edge that is joining a node to itself (self-loop) or one of its ancestor in the tree produced by DFS. 

To find the back edge to any of its ancestors keep a visited array and if there is a back edge to any visited node then there is a loop and return true.

Algorithm:

1. Create the graph using the given number of edges and vertices.
2. Create a recursive function that have current index or vertex, visited array and parent node.
3. Mark the current node as visited .
4. Find all the vertices which are not visited and are adjacent to the current node. Recursively call the function for those vertices, If the recursive function returns true return true.
5. If the adjacent node is not parent and already visited then return true.
6. Create a wrapper function, that calls the recursive function for all the vertices and if any function returns true, return true. (Because all the nodes in the graph might not be connected or reachable from a starting vertex. To make sure every vertex of graph is connected we are calling the recursive function for all unvisited nodes.)
7. Else if for all vertices the function returns false return false.

Dry Run:

Another possible scenario:

6th step in the above algorithm is important for below case

Graph with disconnected components

Implementation:

C++

// A C++ Program to detect
// cycle in an undirected graph
#include <iostream>
#include <limits.h>
#include <list>
using namespace std;

// Class for an undirected graph
class Graph {

    // No. of vertices
    int V;

    // Pointer to an array
    // containing adjacency lists
    list<int>* adj;
    bool isCyclicUtil(int v, bool visited[], int parent);

public:
    // Constructor
    Graph(int V);

    // To add an edge to graph
    void addEdge(int v, int w);

    // Returns true if there is a cycle
    bool isCyclic();
};

Graph::Graph(int V)
{
    this->V = V;
    adj = new list<int>[V];
}

void Graph::addEdge(int v, int w)
{

    // Add w to v’s list.
    adj[v].push_back(w);

    // Add v to w’s list.
    adj[w].push_back(v);
}

// A recursive function that
// uses visited[] and parent to detect
// cycle in subgraph reachable
// from vertex v.
bool Graph::isCyclicUtil(int v, bool visited[], int parent)
{

    // Mark the current node as visited
    visited[v] = true;

    // Recur for all the vertices
    // adjacent to this vertex
    list<int>::iterator i;
    for (i = adj[v].begin(); i != adj[v].end(); ++i) {

        // If an adjacent vertex is not visited,
        // then recur for that adjacent
        if (!visited[*i]) {
            if (isCyclicUtil(*i, visited, v))
                return true;
        }

        // If an adjacent vertex is visited and
        // is not parent of current vertex,
        // then there exists a cycle in the graph.
        else if (*i != parent)
            return true;
    }
    return false;
}

// Returns true if the graph contains
// a cycle, else false.
bool Graph::isCyclic()
{

    // Mark all the vertices as not
    // visited and not part of recursion
    // stack
    bool* visited = new bool[V];
    for (int i = 0; i < V; i++)
        visited[i] = false;

    // Call the recursive helper
    // function to detect cycle in different
    // DFS trees
    for (int u = 0; u < V; u++) {

        // Don't recur for u if
        // it is already visited
        if (!visited[u])
            if (isCyclicUtil(u, visited, -1))
                return true;
    }
    return false;
}

// Driver program to test above functions
int main()
{
    Graph g1(5);
    g1.addEdge(1, 0);
    g1.addEdge(0, 2);
    g1.addEdge(2, 1);
    g1.addEdge(0, 3);
    g1.addEdge(3, 4);
    g1.isCyclic() ? cout << "Graph contains cycle\n"
                  : cout << "Graph doesn't contain cycle\n";

    Graph g2(3);
    g2.addEdge(0, 1);
    g2.addEdge(1, 2);
    g2.isCyclic() ? cout << "Graph contains cycle\n"
                  : cout << "Graph doesn't contain cycle\n";

    return 0;
}

Java

// A Java Program to detect cycle in an undirected graph
import java.io.*;
import java.util.*;
// This class represents a
// directed graph using adjacency list
// representation
class Graph {

    // No. of vertices
    private int V;

    // Adjacency List Representation
    private LinkedList<Integer> adj[];

    // Constructor
    Graph(int v)
    {
        V = v;
        adj = new LinkedList[v];
        for (int i = 0; i < v; ++i)
            adj[i] = new LinkedList();
    }

    // Function to add an edge
    // into the graph
    void addEdge(int v, int w)
    {
        adj[v].add(w);
        adj[w].add(v);
    }

    // A recursive function that
    // uses visited[] and parent to detect
    // cycle in subgraph reachable
    // from vertex v.
    Boolean isCyclicUtil(int v, Boolean visited[],
                         int parent)
    {
        // Mark the current node as visited
        visited[v] = true;
        Integer i;

        // Recur for all the vertices
        // adjacent to this vertex
        Iterator<Integer> it = adj[v].iterator();
        while (it.hasNext()) {
            i = it.next();

            // If an adjacent is not
            // visited, then recur for that
            // adjacent
            if (!visited[i]) {
                if (isCyclicUtil(i, visited, v))
                    return true;
            }

            // If an adjacent is visited
            // and not parent of current
            // vertex, then there is a cycle.
            else if (i != parent)
                return true;
        }
        return false;
    }

    // Returns true if the graph
    // contains a cycle, else false.
    Boolean isCyclic()
    {

        // Mark all the vertices as
        // not visited and not part of
        // recursion stack
        Boolean visited[] = new Boolean[V];
        for (int i = 0; i < V; i++)
            visited[i] = false;

        // Call the recursive helper
        // function to detect cycle in
        // different DFS trees
        for (int u = 0; u < V; u++) {

            // Don't recur for u if already visited
            if (!visited[u])
                if (isCyclicUtil(u, visited, -1))
                    return true;
        }

        return false;
    }

    // Driver method to test above methods
    public static void main(String args[])
    {

        // Create a graph given
        // in the above diagram
        Graph g1 = new Graph(5);
        g1.addEdge(1, 0);
        g1.addEdge(0, 2);
        g1.addEdge(2, 1);
        g1.addEdge(0, 3);
        g1.addEdge(3, 4);
        if (g1.isCyclic())
            System.out.println("Graph
                             contains cycle");
        else
            System.out.println("Graph
                        doesn't contains cycle");

        Graph g2 = new Graph(3);
        g2.addEdge(0, 1);
        g2.addEdge(1, 2);
        if (g2.isCyclic())
            System.out.println("Graph
                             contains cycle");
        else
            System.out.println("Graph
                        doesn't contains cycle");
    }
}
// This code is contributed by Aakash Hasija

Python3

# Python Program to detect cycle in an undirected graph
from collections import defaultdict

# This class represents a undirected
# graph using adjacency list representation


class Graph:

    def __init__(self, vertices):

        # No. of vertices
        self.V = vertices  # No. of vertices

        # Default dictionary to store graph
        self.graph = defaultdict(list)

    # Function to add an edge to graph
    def addEdge(self, v, w):

        # Add w to v_s list
        self.graph[v].append(w)

        # Add v to w_s list
        self.graph[w].append(v)

    # A recursive function that uses
    # visited[] and parent to detect
    # cycle in subgraph reachable from vertex v.
    def isCyclicUtil(self, v, visited, parent):

        # Mark the current node as visited
        visited[v] = True

        # Recur for all the vertices
        # adjacent to this vertex
        for i in self.graph[v]:

            # If the node is not
            # visited then recurse on it
            if visited[i] == False:
                if(self.isCyclicUtil(i, visited, v)):
                    return True
            # If an adjacent vertex is
            # visited and not parent
            # of current vertex,
            # then there is a cycle
            elif parent != i:
                return True

        return False

    # Returns true if the graph
    # contains a cycle, else false.

    def isCyclic(self):

        # Mark all the vertices
        # as not visited
        visited = [False]*(self.V)

        # Call the recursive helper
        # function to detect cycle in different
        # DFS trees
        for i in range(self.V):

            # Don't recur for u if it
            # is already visited
            if visited[i] == False:
                if(self.isCyclicUtil
                   (i, visited, -1)) == True:
                    return True

        return False


# Create a graph given in the above diagram
g = Graph(5)
g.addEdge(1, 0)
g.addEdge(1, 2)
g.addEdge(2, 0)
g.addEdge(0, 3)
g.addEdge(3, 4)

if g.isCyclic():
    print("Graph contains cycle")
else:
    print("Graph does not contain cycle ")
g1 = Graph(3)
g1.addEdge(0, 1)
g1.addEdge(1, 2)


if g1.isCyclic():
    print("Graph contains cycle")
else:
    print("Graph does not contain cycle ")

# This code is contributed by Neelam Yadav

C#

// C# Program to detect cycle in an undirected graph
using System;
using System.Collections.Generic;

// This class represents a directed graph
// using adjacency list representation
class Graph {
    private int V; // No. of vertices

    // Adjacency List Representation
    private List<int>[] adj;

    // Constructor
    Graph(int v)
    {
        V = v;
        adj = new List<int>[ v ];
        for (int i = 0; i < v; ++i)
            adj[i] = new List<int>();
    }

    // Function to add an edge into the graph
    void addEdge(int v, int w)
    {
        adj[v].Add(w);
        adj[w].Add(v);
    }

    // A recursive function that uses visited[]
    // and parent to detect cycle in subgraph
    // reachable from vertex v.
    Boolean isCyclicUtil(int v, Boolean[] visited,
                         int parent)
    {
        // Mark the current node as visited
        visited[v] = true;

        // Recur for all the vertices
        // adjacent to this vertex
        foreach(int i in adj[v])
        {
            // If an adjacent is not visited,
            // then recur for that adjacent
            if (!visited[i]) {
                if (isCyclicUtil(i, visited, v))
                    return true;
            }

            // If an adjacent is visited and
            // not parent of current vertex,
            // then there is a cycle.
            else if (i != parent)
                return true;
        }
        return false;
    }

    // Returns true if the graph contains
    // a cycle, else false.
    Boolean isCyclic()
    {
        // Mark all the vertices as not visited
        // and not part of recursion stack
        Boolean[] visited = new Boolean[V];
        for (int i = 0; i < V; i++)
            visited[i] = false;

        // Call the recursive helper function
        // to detect cycle in different DFS trees
        for (int u = 0; u < V; u++)

            // Don't recur for u if already visited
            if (!visited[u])
                if (isCyclicUtil(u, visited, -1))
                    return true;

        return false;
    }

    // Driver Code
    public static void Main(String[] args)
    {
        // Create a graph given in the above diagram
        Graph g1 = new Graph(5);
        g1.addEdge(1, 0);
        g1.addEdge(0, 2);
        g1.addEdge(2, 1);
        g1.addEdge(0, 3);
        g1.addEdge(3, 4);
        if (g1.isCyclic())
            Console.WriteLine("Graph contains cycle");
        else
            Console.WriteLine(
                "Graph doesn't contains cycle");

        Graph g2 = new Graph(3);
        g2.addEdge(0, 1);
        g2.addEdge(1, 2);
        if (g2.isCyclic())
            Console.WriteLine("Graph contains cycle");
        else
            Console.WriteLine(
                "Graph doesn't contains cycle");
    }
}

// This code is contributed by PrinciRaj1992

Output

Graph contains cycle
Graph doesn't contain cycle

Complexity Analysis:

• Time Complexity: O(V+E). 
  The program does a simple DFS Traversal of the graph which is represented using adjacency list. So the time complexity is O(V+E).
• Space Complexity: O(V). 
  To store the visited array O(V) space is required.

Exercise: Can we use BFS to detect cycle in an undirected graph in O(V+E) time? What about directed graphs?