Detect Cycle in a Directed Graph

Given the root of a Directed graph, The task is to check whether the graph contains a cycle or not. 

Examples:

Input: N = 4, E = 6

Example of graph

Output: Yes
Explanation: The diagram clearly shows a cycle 0 -> 2 -> 0

Input: N = 4, E = 4

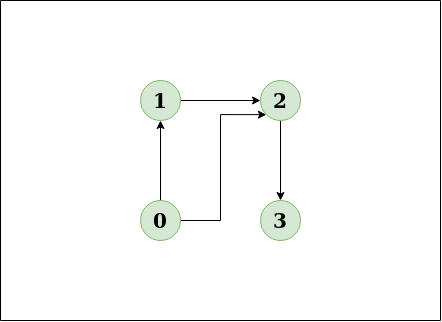
Output: No
Explanation: The diagram clearly shows no cycle

Approach:

The problem can be solved based on the following idea:

To find cycle in a directed graph we can use the Depth First Traversal (DFS) technique. It is based on the idea that there is a cycle in a graph only if there is a back edge [i.e., a node points to one of its ancestors] present in the graph.

To detect a back edge, we need to keep track of the nodes visited till now and the nodes that are in the current recursion stack [i.e., the current path that we are visiting]. If during recursion, we reach a node that is already in the recursion stack, there is a cycle present in the graph.

Note: If the graph is disconnected then get the DFS forest and check for a cycle in individual trees by checking back edges.

Follow the below steps to Implement the idea:

• Create a recursive dfs function that has the following parameters – current vertex, visited array, and recursion stack.
• Mark the current node as visited and also mark the index in the recursion stack.
• Iterate a loop for all the vertices and for each vertex, call the recursive function if it is not yet visited (This step is done to make sure that if there is a forest of graphs, we are checking each forest):
  • In each recursion call, Find all the adjacent vertices of the current vertex which are not visited:
    • If an adjacent vertex is already marked in the recursion stack then return true.
    • Otherwise, call the recursive function for that adjacent vertex.
  • While returning from the recursion call, unmark the current node from the recursion stack, to represent that the current node is no longer a part of the path being traced.
• If any of the functions returns true, stop the future function calls and return true as the answer.

Illustration:

Consider the following graph:

Example of a Directed Graph

Consider we start the iteration from vertex 0.

• Initially, 0 will be marked in both the visited[] and recStack[] array as it is a part of the current path.

Vertex 0 is visited

• Now 0 has two adjacent vertices 1 and 2. Let us consider traversal to the vertex 1. So 1 will be marked in both visited[] and recStack[].

Vertex 1 is visited

• Vertex 1 has only one adjacent vertex. Call the recursive function for 2 and mark it in visited[] and recStack[].

Vertex 2 is visited

• Vertex 2 also has two adjacent vertices. 
  • Vertex 0 is visited and already marked in the recStack[]. So if 0 is checked first, we will get the answer that there is a cycle present.
  • On the other hand, if vertex 3 is checked first, then 3 will be marked in visited[] and recStack[].

Vertex 3 is visited

• While returning from the recursion call for 3, it will be unmarked from recStack[] as it is now not a part of the path currently being traced.

Vertex 3 is unmarked from recStack[]

• Now we have only one option to check, vertex 0, which is already marked in recStack[]. 

So, we can conclude that a cycle exists. We can also find the cycle if we have traversed to vertex 2 from 0 itself in this same way.

Below is the implementation of the above approach:

C++

// A C++ Program to detect cycle in a graph
#include <bits/stdc++.h>
using namespace std;

class Graph {
    // No. of vertices
    int V;

    // Pointer to an array containing adjacency lists
    list<int>* adj;

    // Used by isCyclic()
    bool isCyclicUtil(int v, bool visited[], bool* rs);

public:
    Graph(int V);
    void addEdge(int v, int w);
    bool isCyclic();
};

Graph::Graph(int V)
{
    this->V = V;
    adj = new list<int>[V];
}

void Graph::addEdge(int v, int w)
{
    // Add w to v’s list.
    adj[v].push_back(w);
}

// DFS function to find if a cycle exists
bool Graph::isCyclicUtil(int v, bool visited[],
                         bool* recStack)
{
    if (visited[v] == false) {
        // Mark the current node as visited
        // and part of recursion stack
        visited[v] = true;
        recStack[v] = true;

        // Recur for all the vertices adjacent to this
        // vertex
        list<int>::iterator i;
        for (i = adj[v].begin(); i != adj[v].end(); ++i) {
            if (!visited[*i]
                && isCyclicUtil(*i, visited, recStack))
                return true;
            else if (recStack[*i])
                return true;
        }
    }

    // Remove the vertex from recursion stack
    recStack[v] = false;
    return false;
}

// Returns true if the graph contains a cycle, else false
bool Graph::isCyclic()
{
    // Mark all the vertices as not visited
    // and not part of recursion stack
    bool* visited = new bool[V];
    bool* recStack = new bool[V];
    for (int i = 0; i < V; i++) {
        visited[i] = false;
        recStack[i] = false;
    }

    // Call the recursive helper function
    // to detect cycle in different DFS trees
    for (int i = 0; i < V; i++)
        if (!visited[i]
            && isCyclicUtil(i, visited, recStack))
            return true;

    return false;
}

// Driver code
int main()
{
    // Create a graph
    Graph g(4);
    g.addEdge(0, 1);
    g.addEdge(0, 2);
    g.addEdge(1, 2);
    g.addEdge(2, 0);
    g.addEdge(2, 3);
    g.addEdge(3, 3);

    // Function call
    if (g.isCyclic())
        cout << "Graph contains cycle";
    else
        cout << "Graph doesn't contain cycle";
    return 0;
}

Java

// A Java Program to detect cycle in a graph
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;

class Graph {

    private final int V;
    private final List<List<Integer>> adj;

    public Graph(int V)
    {
        this.V = V;
        adj = new ArrayList<>(V);

        for (int i = 0; i < V; i++)
            adj.add(new LinkedList<>());
    }

    // Function to check if cycle exists
    private boolean isCyclicUtil(int i, boolean[] visited,
                                      boolean[] recStack)
    {

        // Mark the current node as visited and
        // part of recursion stack
        if (recStack[i])
            return true;

        if (visited[i])
            return false;

        visited[i] = true;

        recStack[i] = true;
        List<Integer> children = adj.get(i);

        for (Integer c: children)
            if (isCyclicUtil(c, visited, recStack))
                return true;

        recStack[i] = false;

        return false;
    }

    private void addEdge(int source, int dest) {
        adj.get(source).add(dest);
    }

    // Returns true if the graph contains a
    // cycle, else false.
    private boolean isCyclic()
    {
        // Mark all the vertices as not visited and
        // not part of recursion stack
        boolean[] visited = new boolean[V];
        boolean[] recStack = new boolean[V];

        // Call the recursive helper function to
        // detect cycle in different DFS trees
        for (int i = 0; i < V; i++)
            if (isCyclicUtil(i, visited, recStack))
                return true;

        return false;
    }

    // Driver code
    public static void main(String[] args)
    {
        Graph graph = new Graph(4);
        graph.addEdge(0, 1);
        graph.addEdge(0, 2);
        graph.addEdge(1, 2);
        graph.addEdge(2, 0);
        graph.addEdge(2, 3);
        graph.addEdge(3, 3);

        // Function call
        if(graph.isCyclic())
            System.out.println("Graph contains cycle");
        else
            System.out.println("Graph doesn't "
                                    + "contain cycle");
    }
}

// This code is contributed by Sagar Shah.

Python3

# Python program to detect cycle
# in a graph

from collections import defaultdict


class Graph():
    def __init__(self, vertices):
        self.graph = defaultdict(list)
        self.V = vertices

    def addEdge(self, u, v):
        self.graph[u].append(v)

    def isCyclicUtil(self, v, visited, recStack):

        # Mark current node as visited and
        # adds to recursion stack
        visited[v] = True
        recStack[v] = True

        # Recur for all neighbours
        # if any neighbour is visited and in
        # recStack then graph is cyclic
        for neighbour in self.graph[v]:
            if visited[neighbour] == False:
                if self.isCyclicUtil(neighbour, visited, recStack) == True:
                    return True
            elif recStack[neighbour] == True:
                return True

        # The node needs to be popped from
        # recursion stack before function ends
        recStack[v] = False
        return False

    # Returns true if graph is cyclic else false
    def isCyclic(self):
        visited = [False] * (self.V + 1)
        recStack = [False] * (self.V + 1)
        for node in range(self.V):
            if visited[node] == False:
                if self.isCyclicUtil(node, visited, recStack) == True:
                    return True
        return False


# Driver code
if __name__ == '__main__':
    g = Graph(4)
    g.addEdge(0, 1)
    g.addEdge(0, 2)
    g.addEdge(1, 2)
    g.addEdge(2, 0)
    g.addEdge(2, 3)
    g.addEdge(3, 3)

    if g.isCyclic() == 1:
        print("Graph contains cycle")
    else:
        print("Graph doesn't contain cycle")

# Thanks to Divyanshu Mehta for contributing this code

C#

// A C# Program to detect cycle in a graph
using System;
using System.Collections.Generic;

public class Graph {

    private readonly int V;
    private readonly List<List<int> > adj;

    public Graph(int V)
    {
        this.V = V;
        adj = new List<List<int> >(V);

        for (int i = 0; i < V; i++)
            adj.Add(new List<int>());
    }

    // Function to check if cycle exists
    private bool isCyclicUtil(int i, bool[] visited,
                              bool[] recStack)
    {
        // Mark the current node as visited and
        // part of recursion stack
        if (recStack[i])
            return true;

        if (visited[i])
            return false;

        visited[i] = true;

        recStack[i] = true;
        List<int> children = adj[i];

        foreach(int c in children) if (
            isCyclicUtil(c, visited, recStack)) return true;

        recStack[i] = false;

        return false;
    }

    private void addEdge(int sou, int dest)
    {
        adj[sou].Add(dest);
    }

    // Returns true if the graph contains a
    // cycle, else false
    private bool isCyclic()
    {
        // Mark all the vertices as not visited and
        // not part of recursion stack
        bool[] visited = new bool[V];
        bool[] recStack = new bool[V];

        // Call the recursive helper function to
        // detect cycle in different DFS trees
        for (int i = 0; i < V; i++)
            if (isCyclicUtil(i, visited, recStack))
                return true;

        return false;
    }

    // Driver code
    public static void Main(String[] args)
    {
        Graph graph = new Graph(4);
        graph.addEdge(0, 1);
        graph.addEdge(0, 2);
        graph.addEdge(1, 2);
        graph.addEdge(2, 0);
        graph.addEdge(2, 3);
        graph.addEdge(3, 3);

        // Function call
        if (graph.isCyclic())
            Console.WriteLine("Graph contains cycle");
        else
            Console.WriteLine("Graph doesn't "
                              + "contain cycle");
    }
}

// This code contributed by Rajput-Ji

Javascript

// A JavaScript Program to detect cycle in a graph

let V;
let adj=[];
function Graph(v)
{
    V=v;
    for (let i = 0; i < V; i++)
        adj.push([]);
}

// Function to check if cycle exists
function isCyclicUtil(i,visited,recStack)
{
    // Mark the current node as visited and
    // part of recursion stack
        if (recStack[i])
            return true;

        if (visited[i])
            return false;

        visited[i] = true;

        recStack[i] = true;
        let children = adj[i];

        for (let c=0;c< children.length;c++)
            if (isCyclicUtil(children, visited, recStack))
                return true;

        recStack[i] = false;

        return false;
}

function addEdge(source,dest)
{
    adj .push(dest);
}

// Returns true if the graph contains a
// cycle, else false.
function isCyclic()
{
    // Mark all the vertices as not visited and
        // not part of recursion stack
        let visited = new Array(V);
        let recStack = new Array(V);
        for(let i=0;i<V;i++)
        {
            visited[i]=false;
            recStack[i]=false;
        }


        // Call the recursive helper function to
        // detect cycle in different DFS trees
        for (let i = 0; i < V; i++)
            if (isCyclicUtil(i, visited, recStack))
                return true;

        return false;
}

// Driver code
Graph(4);
addEdge(0, 1);
addEdge(0, 2);
addEdge(1, 2);
addEdge(2, 0);
addEdge(2, 3);
addEdge(3, 3);

if(isCyclic())
    console.log("Graph contains cycle");
else
    console.log("Graph doesn't "
                   + "contain cycle");


// This code is contributed by patel2127

Output

Graph contains cycle

Time Complexity: O(V + E), the Time Complexity of this method is the same as the time complexity of DFS traversal which is O(V+E).
Auxiliary Space: O(V). To store the visited and recursion stack O(V) space is needed.

In the below article, another O(V + E) method is discussed : 
Detect Cycle in a direct graph using colors

Another Approcah:

Using Kahn’s Algorithm:

For arranging the vertices of a directed acyclic graph (DAG) such that for every directed edge from vertex A to vertex B, A occurs before B in the ordering, Kahn’s algorithm is a well-known approach for topological sorting.

The first step of Kahn’s technique is to identify all the vertices that have no dependencies and have zero incoming edges. These vertices are then taken out of the graph and added to the output list. The remaining vertices are subjected to the same procedure, with each iteration eliminating the vertices with no incoming edges until all vertices have been handled.

The algorithm operates on the premise that a vertex can be visited securely and added to the output list if it doesn’t have any incoming edges. The problem is transformed into a smaller DAG by eliminating this vertex, which also eliminates all of its outgoing edges. Each vertex’s incoming edges are tracked by the algorithm, which updates them when vertices are dropped.

The algorithm is explained in detail below:

1. Calculate the in-degree (number of incoming edges) for each vertex in the DAG and set the starting value of the visited nodes count to 0.
2. Select all of the vertices with in-degree values of 0, then enqueue them all.
3. Add one more visited node to the count after removing a vertex from the queue (Dequeue operation).
4. For each of its neighbouring nodes or vertices, reduce in-degree by 1.
5. Add a node or vertex to the queue if the in-degree of any nearby nodes or vertices is lowered to zero.
6. Up until the queue is empty, repeat step 3.
7. The topological sort is not possible for the provided graph if the number of visited nodes is not equal to the number of graph vertices.
   

Explanation:

The Graph class has been implemented in below code, and the graph is represented as an adjacency list. Additionally, a method called isCyclic that runs a BFS traversal of the graph in order to find cycles has been defined. Prior to enqueuing vertices with a 0 in-degree, the isCyclic function determines the in-degree of each vertex. Then it eliminates vertices with 0 in-degree and lowers the in-degree of the vertices next to them. Any adjacent vertex that has an in-degree of 0 is enqueued. If not all vertices are visited, indicating a cycle, the method returns true and keeps track of the number of visited vertices.

C++

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

class Graph {
private:
    int V; // number of vertices
    vector<vector<int>> adj; // adjacency list

public:
    Graph(int V) {
        this->V = V;
        adj.resize(V);
    }

    void addEdge(int v, int w) {
        adj[v].push_back(w);
    }

    bool isCyclic() {
        vector<int> inDegree(V, 0); // stores in-degree of each vertex
        queue<int> q; // queue to store vertices with 0 in-degree
        int visited = 0; // count of visited vertices

        // calculate in-degree of each vertex
        for (int u = 0; u < V; u++) {
            for (auto v : adj[u]) {
                inDegree[v]++;
            }
        }

        // enqueue vertices with 0 in-degree
        for (int u = 0; u < V; u++) {
            if (inDegree[u] == 0) {
                q.push(u);
            }
        }

        // BFS traversal
        while (!q.empty()) {
            int u = q.front();
            q.pop();
            visited++;

            // reduce in-degree of adjacent vertices
            for (auto v : adj[u]) {
                inDegree[v]--;
                // if in-degree becomes 0, enqueue the vertex
                if (inDegree[v] == 0) {
                    q.push(v);
                }
            }
        }

        return visited != V; // if not all vertices are visited, there is a cycle
    }
};

int main() {
    Graph g(6);
    g.addEdge(0, 1);
    g.addEdge(0, 2);
    g.addEdge(1, 3);
    g.addEdge(4, 1);
    g.addEdge(4, 5);
    g.addEdge(5, 3);

    if (g.isCyclic()) {
        cout << "Graph contains cycle." << endl;
    } else {
        cout << "Graph does not contain cycle." << endl;
    }

    return 0;
}

Output

Graph does not contain cycle.

Time Complexity: O(V + E), the Time Complexity of this method is the same as the time complexity of DFS traversal which is O(V+E).
Auxiliary Space: O(V). To store the visited and recursion stack O(V) space is needed.