Detect Cycle in a directed graph using colors
Last Updated :
30 Jun, 2022
Given a directed graph, check whether the graph contains a cycle or not. Your function should return true if the given graph contains at least one cycle, else return false.
Example:
Input: n = 4, e = 6
0 -> 1, 0 -> 2, 1 -> 2, 2 -> 0, 2 -> 3, 3 -> 3
Output: Yes
Explanation:
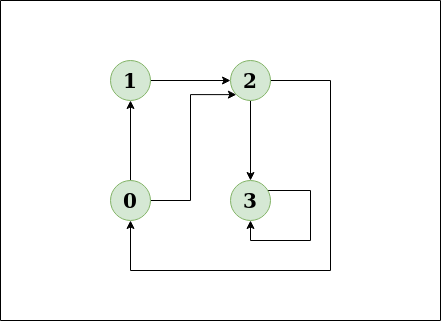
This diagram clearly shows a cycle 0 -> 2 -> 0.
Input:n = 4, e = 3
0 -> 1, 0 -> 2, 1 -> 2, 2 -> 3
Output:No
Explanation:
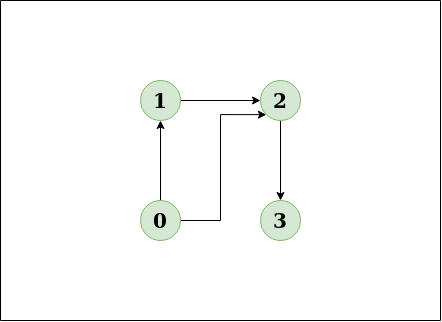
This diagram clearly shows no cycle.
Solution
Approach: Depth First Traversal can be used to detect cycle in a Graph. DFS for a connected graph produces a tree. There is a cycle in a graph only if there is a back edge present in the graph. A back edge is an edge that is from a node to itself (selfloop) or one of its ancestor in the tree produced by DFS. In the following graph, there are 3 back edges, marked with cross sign. It can be observed that these 3 back edges indicate 3 cycles present in the graph.
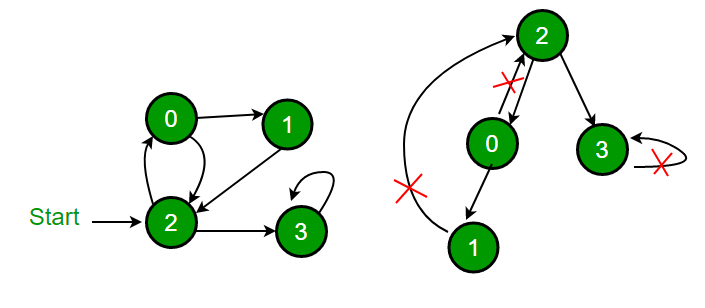
For a disconnected graph, we get the DFS forest as output. To detect cycle, we can check for cycle in individual trees by checking back edges.
In the previous post, we have discussed a solution that stores visited vertices in a separate array which stores vertices of the current recursion call stack.
In this post, a different solution is discussed. The solution is from CLRS book. The idea is to do DFS of a given graph and while doing traversal, assign one of the below three colours to every vertex.
WHITE : Vertex is not processed yet. Initially, all vertices are WHITE.
GRAY: Vertex is being processed (DFS for this vertex has started, but not finished which means that all descendants (in DFS tree) of this vertex are not processed yet (or this vertex is in the function call stack)
BLACK : Vertex and all its descendants are processed. While doing DFS, if an edge is encountered from current vertex to a GRAY vertex, then this edge is back edge and hence there is a cycle.
Algorithm:
- Create a recursive function that takes the edge and color array (this can be also kept as a global variable)
- Mark the current node as GREY.
- Traverse all the adjacent nodes and if any node is marked GREY then return true as a loop is bound to exist.
- If any adjacent vertex is WHITE then call the recursive function for that node. If the function returns true. Return true.
- If no adjacent node is grey or has not returned true then mark the current Node as BLACK and return false.
Implementation:
C++
#include <bits/stdc++.h>
using namespace std;
enum Color {WHITE, GRAY, BLACK};
class Graph
{
int V;
list<int>* adj;
bool DFSUtil(int v, int color[]);
public:
Graph(int V);
void addEdge(int v, int w);
bool isCyclic();
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w);
}
bool Graph::DFSUtil(int u, int color[])
{
color[u] = GRAY;
list<int>::iterator i;
for (i = adj[u].begin(); i != adj[u].end(); ++i)
{
int v = *i;
if (color[v] == GRAY)
return true;
if (color[v] == WHITE && DFSUtil(v, color))
return true;
}
color[u] = BLACK;
return false;
}
bool Graph::isCyclic()
{
int *color = new int[V];
for (int i = 0; i < V; i++)
color[i] = WHITE;
for (int i = 0; i < V; i++)
if (color[i] == WHITE)
if (DFSUtil(i, color) == true)
return true;
return false;
}
int main()
{
Graph g(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
if (g.isCyclic())
cout << "Graph contains cycle";
else
cout << "Graph doesn't contain cycle";
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG
{
static int WHITE = 0, GRAY = 1, BLACK = 2;
static class Graph
{
int V;
LinkedList<Integer>[] adjList;
Graph(int ver)
{
V = ver;
adjList = new LinkedList[V];
for (int i = 0; i < V; i++)
adjList[i] = new LinkedList<>();
}
}
static void addEdge(Graph g, int u, int v)
{
g.adjList[u].add(v);
}
static boolean DFSUtil(Graph g, int u, int[] color)
{
color[u] = GRAY;
for (Integer in : g.adjList[u])
{
if (color[in] == GRAY)
return true;
if (color[in] == WHITE && DFSUtil(g, in, color) == true)
return true;
}
color[u] = BLACK;
return false;
}
static boolean isCyclic(Graph g)
{
int[] color = new int[g.V];
for (int i = 0; i < g.V; i++)
{
color[i] = WHITE;
}
for (int i = 0; i < g.V; i++)
{
if (color[i] == WHITE)
{
if(DFSUtil(g, i, color) == true)
return true;
}
}
return false;
}
public static void main(String args[])
{
Graph g = new Graph(4);
addEdge(g, 0, 1);
addEdge(g, 0, 2);
addEdge(g, 1, 2);
addEdge(g, 2, 0);
addEdge(g, 2, 3);
addEdge(g, 3, 3);
if (isCyclic(g))
System.out.println("Graph contains cycle");
else
System.out.println("Graph doesn't contain cycle");
}
}
|
Python3
from collections import defaultdict
class Graph():
def __init__(self, V):
self.V = V
self.graph = defaultdict(list)
def addEdge(self, u, v):
self.graph[u].append(v)
def DFSUtil(self, u, color):
color[u] = "GRAY"
for v in self.graph[u]:
if color[v] == "GRAY":
return True
if color[v] == "WHITE" and self.DFSUtil(v, color) == True:
return True
color[u] = "BLACK"
return False
def isCyclic(self):
color = ["WHITE"] * self.V
for i in range(self.V):
if color[i] == "WHITE":
if self.DFSUtil(i, color) == True:
return True
return False
g = Graph(4)
g.addEdge(0, 1)
g.addEdge(0, 2)
g.addEdge(1, 2)
g.addEdge(2, 0)
g.addEdge(2, 3)
g.addEdge(3, 3)
print ("Graph contains cycle" if g.isCyclic() == True\
else "Graph doesn't contain cycle")
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static int WHITE = 0, GRAY = 1, BLACK = 2;
public class Graph
{
public int V;
public List<int>[] adjList;
public Graph(int ver)
{
V = ver;
adjList = new List<int>[V];
for (int i = 0; i < V; i++)
adjList[i] = new List<int>();
}
}
static void addEdge(Graph g, int u, int v)
{
g.adjList[u].Add(v);
}
static bool DFSUtil(Graph g, int u, int[] color)
{
color[u] = GRAY;
foreach (int iN in g.adjList[u])
{
if (color[iN] == GRAY)
return true;
if (color[iN] == WHITE &&
DFSUtil(g, iN, color) == true)
return true;
}
color[u] = BLACK;
return false;
}
static bool isCyclic(Graph g)
{
int[] color = new int[g.V];
for (int i = 0; i < g.V; i++)
{
color[i] = WHITE;
}
for (int i = 0; i < g.V; i++)
{
if (color[i] == WHITE)
{
if(DFSUtil(g, i, color) == true)
return true;
}
}
return false;
}
public static void Main(String []args)
{
Graph g = new Graph(4);
addEdge(g, 0, 1);
addEdge(g, 0, 2);
addEdge(g, 1, 2);
addEdge(g, 2, 0);
addEdge(g, 2, 3);
addEdge(g, 3, 3);
if (isCyclic(g))
Console.WriteLine("Graph contains cycle");
else
Console.WriteLine("Graph doesn't contain cycle");
}
}
|
Javascript
<script>
var WHITE = 0, GRAY = 1, BLACK = 2;
class Graph
{
constructor(ver)
{
this.V = ver;
this.adjList = Array.from(
Array(this.V), () => Array(this.V));
}
}
function addEdge(g, u, v)
{
g.adjList[u].push(v);
}
function DFSUtil(g, u, color)
{
color[u] = GRAY;
for(var iN of g.adjList[u])
{
if (color[iN] == GRAY)
return true;
if (color[iN] == WHITE &&
DFSUtil(g, iN, color) == true)
return true;
}
color[u] = BLACK;
return false;
}
function isCyclic(g)
{
var color = Array(g.V);
for(var i = 0; i < g.V; i++)
{
color[i] = WHITE;
}
for(var i = 0; i < g.V; i++)
{
if (color[i] == WHITE)
{
if (DFSUtil(g, i, color) == true)
return true;
}
}
return false;
}
var g = new Graph(4);
addEdge(g, 0, 1);
addEdge(g, 0, 2);
addEdge(g, 1, 2);
addEdge(g, 2, 0);
addEdge(g, 2, 3);
addEdge(g, 3, 3);
if (isCyclic(g))
document.write("Graph contains cycle");
else
document.write("Graph doesn't contain cycle");
</script>
|
Output
Graph contains cycle
Complexity Analysis:
- Time complexity: O(V + E), where V is the number of vertices and E is the number of edges in the graph.
- Space Complexity :O(V).
Since an extra color array is needed of size V.
Share your thoughts in the comments
Please Login to comment...