Computer Organization | Amdahl’s law and its proof
Last Updated :
14 May, 2023
It is named after computer scientist Gene Amdahl( a computer architect from IBM and Amdahl corporation) and was presented at the AFIPS Spring Joint Computer Conference in 1967. It is also known as Amdahl’s argument. It is a formula that gives the theoretical speedup in latency of the execution of a task at a fixed workload that can be expected of a system whose resources are improved. In other words, it is a formula used to find the maximum improvement possible by just improving a particular part of a system. It is often used in parallel computing to predict the theoretical speedup when using multiple processors. Speedup- Speedup is defined as the ratio of performance for the entire task using the enhancement and performance for the entire task without using the enhancement or speedup can be defined as the ratio of execution time for the entire task without using the enhancement and execution time for the entire task using the enhancement. If Pe is the performance for the entire task using the enhancement when possible, Pw is the performance for the entire task without using the enhancement, Ew is the execution time for the entire task without using the enhancement and Ee is the execution time for the entire task using the enhancement when possible then, Speedup = Pe/Pw or Speedup = Ew/Ee Amdahl’s law uses two factors to find speedup from some enhancement:
- Fraction enhanced – The fraction of the computation time in the original computer that can be converted to take advantage of the enhancement. For example- if 10 seconds of the execution time of a program that takes 40 seconds in total can use an enhancement, the fraction is 10/40. This obtained value is Fraction Enhanced. Fraction enhanced is always less than 1.
- Speedup enhanced – The improvement gained by the enhanced execution mode; that is, how much faster the task would run if the enhanced mode were used for the entire program. For example – If the enhanced mode takes, say 3 seconds for a portion of the program, while it is 6 seconds in the original mode, the improvement is 6/3. This value is Speedup enhanced. Speedup Enhanced is always greater than 1.
The overall Speedup is the ratio of the execution time:-  Proof:- Let Speedup be S, old execution time be T, new execution time be T’, execution time that is taken by portion A(that will be enhanced) is t, execution time that is taken by portion A(after enhancing) is t’, execution time that is taken by the portion that won’t be enhanced is tn, Fraction enhanced is f’, Speedup enhanced is S’. Now from the above equation,
Proof:- Let Speedup be S, old execution time be T, new execution time be T’, execution time that is taken by portion A(that will be enhanced) is t, execution time that is taken by portion A(after enhancing) is t’, execution time that is taken by the portion that won’t be enhanced is tn, Fraction enhanced is f’, Speedup enhanced is S’. Now from the above equation, 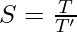 [Tex]T=t_{n}+ t [/Tex]
[Tex]T=t_{n}+ t [/Tex]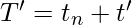 [Tex]f’ = \frac{t}{T} [/Tex]
[Tex]f’ = \frac{t}{T} [/Tex]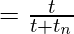 [Tex]1-f’= 1- \frac{t}{t+t_{n}} [/Tex]
[Tex]1-f’= 1- \frac{t}{t+t_{n}} [/Tex]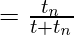 [Tex]S’=\frac{t}{t’} [/Tex]
[Tex]S’=\frac{t}{t’} [/Tex]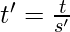 [Tex]=\frac{T*f’}{S’} [/Tex]
[Tex]=\frac{T*f’}{S’} [/Tex]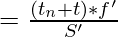 [Tex]=\frac{t’}{t_{n}+t}=\frac{f’}{S’} [/Tex]
[Tex]=\frac{t’}{t_{n}+t}=\frac{f’}{S’} [/Tex]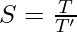 [Tex]= \frac{t_{n}+t}{t_{n}+t’} [/Tex]
[Tex]= \frac{t_{n}+t}{t_{n}+t’} [/Tex]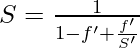 [Tex]Overall Speedup = \frac{1}{1 – Fraction Enhanced + ( Fraction Enhanced/Speedup Enhanced )} [/Tex]Hence proved.
[Tex]Overall Speedup = \frac{1}{1 – Fraction Enhanced + ( Fraction Enhanced/Speedup Enhanced )} [/Tex]Hence proved.
Say the for the fraction f when parallelized gave us the above formula. Then what would be to find the maximum overall speedup of a system when we use parallelism? To compute this just put speedup enhanced –>(tending to) infinity.
Then the formula reduces to:
Overall Speedup(max) = 1/{1 – FractionEnhanced}
Of course, this is just theoretical(ideal) and is not achievable in real-life conditions.
Likewise, we can also think of the case where f = 1.
Amdahl’s law is a principle that states that the maximum potential improvement to the performance of a system is limited by the portion of the system that cannot be improved. In other words, the performance improvement of a system as a whole is limited by its bottlenecks.
The law is often used to predict the potential performance improvement of a system when adding more processors or improving the speed of individual processors. It is named after Gene Amdahl, who first proposed it in 1967.
The formula for Amdahl’s law is:
S = 1 / (1 – P + (P / N))
Where:
S is the speedup of the system
P is the proportion of the system that can be improved
N is the number of processors in the system
For example, if a system has a single bottleneck that occupies 20% of the total execution time, and we add 4 more processors to the system, the speedup would be:
S = 1 / (1 – 0.2 + (0.2 / 5))
S = 1 / (0.8 + 0.04)
S = 1 / 0.84
S = 1.19
This means that the overall performance of the system would improve by about 19% with the addition of the 4 processors.
It’s important to note that Amdahl’s law assumes that the rest of the system is able to fully utilize the additional processors, which may not always be the case in practice.
Advantages of Amdahl’s law:
- Provides a way to quantify the maximum potential speedup that can be achieved by parallelizing a program, which can help guide decisions about hardware and software design.
- Helps to identify the portions of a program that are not easily parallelizable, which can guide efforts to optimize those portions of the code.
- Provides a framework for understanding the trade-offs between parallelization and other forms of optimization, such as code optimization and algorithmic improvements.
Disadvantages of Amdahl’s law:
- Assumes that the portion of the program that cannot be parallelized is fixed, which may not be the case in practice. For example, it is possible to optimize code to reduce the portion of the program that cannot be parallelized, making Amdahl’s law less accurate.
- Assumes that all processors have the same performance characteristics, which may not be the case in practice. For example, in a heterogeneous computing environment, some processors may be faster than others, which can affect the potential speedup that can be achieved.
- Does not take into account other factors that can affect the performance of parallel programs, such as communication overhead and load balancing. These factors can impact the actual speedup that is achieved in practice, which may be lower than the theoretical maximum predicted by Amdahl’s law.
Share your thoughts in the comments
Please Login to comment...