Question 14: 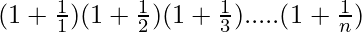 = (n+1)
= (n+1)
Solution:
We have,
P(n) = 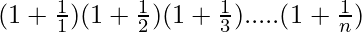 = (n+1)
= (n+1)
For n=1, we get
P(1) = (1+ 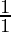 ) = 2 = (1+1) = 2
) = 2 = (1+1) = 2
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = 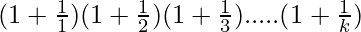 = (k+1) ……………..(1)
= (k+1) ……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = 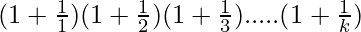
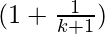
= (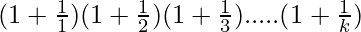 )
) 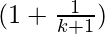
From Eq(1), we get
= (k+1) (1+ 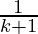 )
)
= (k+1) 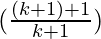
= {(k+1)+1}
Hence,
P(k+1) = {(k+1)+1}
Thus P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
Question 15: 12 + 32 + 52 + …… + (2n-1)2 = 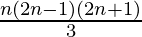
Solution:
We have,
P(n) = 12 + 32 + 52 + …… + (2n-1)2 = 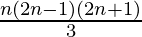
For n=1, we get
P(1) = 12 = 1 = 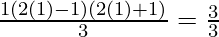 = 1
= 1
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = 12 + 32 + 52 + …… + (2k-1)2 = 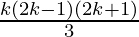 ……………..(1)
……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = 12 + 32 + 52 + …… + (2k-1)2 + (2(k+1)-1)2
= (12 + 32 + 52 + …… + (2k-1)2) + (2k+1)2
From Eq(1), we get
= 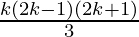 + (2k+1)2
+ (2k+1)2
= (2k+1) 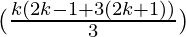
= (2k+1) 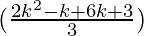
= (2k+1) 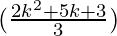
= (2k+1) 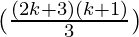
= 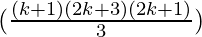
= 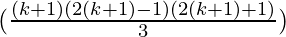
Hence,
P(k+1) = 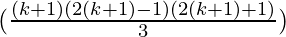
Thus P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
Question 16: 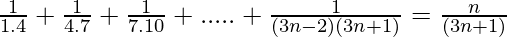
Solution:
We have,
P(n) = 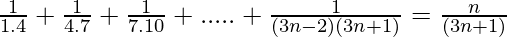
For n=1, we get
P(1) = 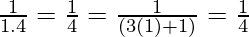
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = 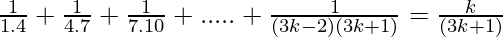 ……………..(1)
……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = 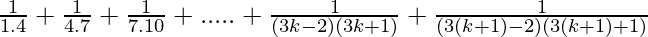
= (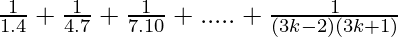 )
) 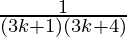
From Eq(1), we get
= 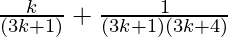
= 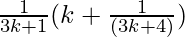
= 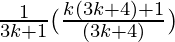
= 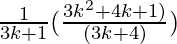
= 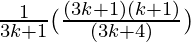
= 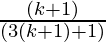
Hence,
P(k+1) = 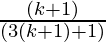
Thus P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
Question 17: 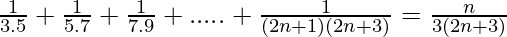
Solution:
We have,
P(n) = 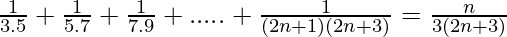
For n=1, we get
P(1) = 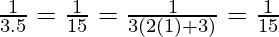
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = 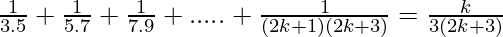 ……………..(1)
……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = 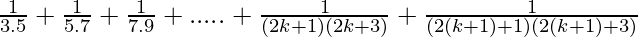
= (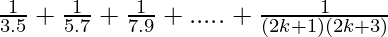 )
) 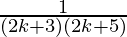
From Eq(1), we get
= 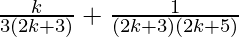
= 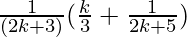
= 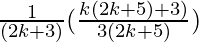
= 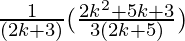
= 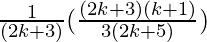
= 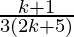
= 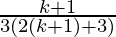
Hence,
P(k+1) = 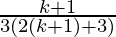
Thus P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
Question 18: 1 + 2 + 3 + ….. + n < 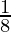 (2n+1)2
(2n+1)2
Solution:
We have,
P(n) = 1 + 2 + 3 + ….. + n < 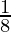 (2n+1)2
(2n+1)2
For n=1, we get
P(1) = 1 < 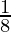 (2(1)+1)2
(2(1)+1)2
1 < 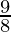
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = 1 + 2 + 3 + ….. + k < 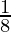 (2k+1)2 ……………..(1)
(2k+1)2 ……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = 1 + 2 + 3 + ….. + k + (k+1)
= (1 + 2 + 3 + ….. + k) + k+1 < 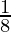 (2k+1)2 + (k+1)
(2k+1)2 + (k+1)
< 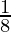 ((2k+1)2 + 8(k+1))
((2k+1)2 + 8(k+1))
< 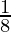 ((4k2+4k+1) + 8k+8))
((4k2+4k+1) + 8k+8))
< 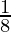 (4k2+12k+9)
(4k2+12k+9)
< 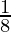 (2k+3)2
(2k+3)2
P(k+1) < 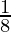 (2(k+1)+1)2
(2(k+1)+1)2
Thus P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
Question 19: n (n + 1) (n + 5) is a multiple of 3.
Solution:
We have,
P (n) = n (n + 1) (n + 5), which is a multiple of 3
For n=1, we get
p(1) = 1 (1 + 1) (1 + 5) = 12, which is a multiple of 3
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = k (k + 1) (k + 5) is a multiple of 3
P(k) = k (k + 1) (k + 5) = 3m, where m ∈ N ………… (1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = (k + 1) {(k + 1) + 1} {(k + 1) + 5}
= (k + 1) (k + 2) {(k + 5) + 1}
By multiplying the terms
= (k + 1) (k + 2) (k + 5) + (k + 1) (k + 2)
= {k (k + 1) (k + 5) + 2 (k + 1) (k + 5)} + (k + 1) (k + 2)
Using Eq(1), we get
= 3m + (k + 1) {2 (k + 5) + (k + 2)}
= 3m + (k + 1) {2k + 10 + k + 2}
= 3m + (k + 1) (3k + 12)
= 3m + 3 (k + 1) (k + 4)
= 3 {m + (k + 1) (k + 4)}
= 3 × q (where q = {m + (k + 1) (k + 4)} is some natural number)
(k + 1) {(k + 1) + 1} {(k + 1) + 5} is a multiple of 3
Thus P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
Question 20: 102n – 1 + 1 is divisible by 11.
Solution:
We have,
P (n): 102n – 1 + 1 is divisible by 11
For n=1, we get
P (1) = 102.1 – 1 + 1 = 11, which is divisible by 11
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
102k – 1 + 1 is divisible by 11
102k – 1 + 1 = 11m, where m ∈ N …………… (1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k + 1) = 10 2(k + 1) – 1 + 1
= 102k + 2 – 1 + 1
= 102k + 1 + 1
= 102 (102k-1 + 1 – 1) + 1
= 102 (102k-1 + 1) – 102 + 1
Using Eq(1), we get
= 102. 11m – 100 + 1
= 100 × 11m – 99
Taking out the common terms
= 11 (100m – 9)
= 11r, where r = (100m – 9) is some natural number
10 2(k + 1) – 1 + 1 is divisible by 11
P (k + 1) is true whenever P (k) is true.
Therefore, by the principle of mathematical induction, statement P (n) is true for all natural numbers i.e. n.
Question 21: x2n – y2n is divisible by x + y.
Solution:
We have,
P (n) = x2n – y2n is divisible by x + y
For n=1, we get
P (1) = x2 × 1 – y2 × 1 = x2 – y2 = (x + y) (x – y), which is divisible by (x + y)
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
x2k – y2k is divisible by x + y
x2k – y2k = m (x + y), where m ∈ N …… (1)
Let’s prove that P(k + 1) is also true. Now, we have
x 2(k + 1) – y 2(k + 1)
= x 2k . x2 – y2k . y2
By adding and subtracting y2k we get
= x2 (x2k – y2k + y2k) – y2k. y2
Using Eq(1), we get
= x2 {m (x + y) + y2k} – y2k. y2
= m (x + y) x2 + y2k. x2 – y2k. y2
Taking out the common terms
= m (x + y) x2 + y2k (x2 – y2)
= m (x + y) x2 + y2k (x + y) (x – y)
So we get
= (x + y) {mx2 + y2k (x – y)}, which is a factor of (x + y)
P (k + 1) is true whenever P (k) is true.
Therefore, by the principle of mathematical induction, statement P (n) is true for all natural numbers i.e. n.
Question 22: 32n+2 – 8n – 9 is divisible by 8.
Solution:
We have,
P (n) = 32n + 2 – 8n – 9 is divisible by 8
For n=1, we get
P (1) = 32 × 1 + 2 – 8 × 1 – 9 = 64, which is divisible by 8
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
32k + 2 – 8k – 9 is divisible by 8
32k + 2 – 8k – 9 = 8m, where m ∈ N …… (1)
Let’s prove that P(k + 1) is also true. Now, we have
3 2(k + 1) + 2 – 8 (k + 1) – 9
= 3 2k + 2 . 32 – 8k – 8 – 9
By adding and subtracting 8k and 9 we get
= 32 (32k + 2 – 8k – 9 + 8k + 9) – 8k – 17
= 32 (32k + 2 – 8k – 9) + 32 (8k + 9) – 8k – 17
Using Eq(1), we get
= 9. 8m + 9 (8k + 9) – 8k – 17
= 9. 8m + 72k + 81 – 8k – 17
= 9. 8m + 64k + 64
By taking out the common terms
= 8 (9m + 8k + 8)
= 8r, where r = (9m + 8k + 8) is a natural number
So 3 2(k + 1) + 2 – 8 (k + 1) – 9 is divisible by 8
P (k + 1) is true whenever P (k) is true.
Therefore, by the principle of mathematical induction, statement P (n) is true for all natural numbers i.e. n.
Question 23: 41n – 14n is a multiple of 27.
Solution:
We have,
P (n) = 41n – 14n is a multiple of 27
For n=1, we get
P (1) = 411 – 141 = 27, which is a multiple by 27
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
41k – 14k is a multiple of 27
41k – 14k = 27m, where m ∈ N …… (1)
Let’s prove that P(k + 1) is also true. Now, we have
41k + 1 – 14k + 1
= 41k. 41 – 14k. 14
By adding and subtracting 14k we get
= 41 (41k – 14k + 14k) – 14k. 14
= 41 (41k – 14k) + 41. 14k – 14k. 14
Using Eq(1), we get
= 41. 27m + 14k ( 41 – 14)
= 41. 27m + 27. 14k
By taking out the common terms
= 27 (41m – 14k)
= 27r, where r = (41m – 14k) is a natural number
So 41k + 1 – 14k + 1 is a multiple of 27
P (k + 1) is true whenever P (k) is true.
Therefore, by the principle of mathematical induction, statement P (n) is true for all natural numbers i.e. n.
Question 24: (2n + 7) < (n + 3)2.
Solution:
We have,
P(n) = (2n +7) < (n + 3)2
For n=1, we get
2.1 + 7 = 9 < (1 + 3)2 = 16
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
(2k + 7) < (k + 3)2 … (1)
Let’s prove that P(k + 1) is also true. Now, we have
{2 (k + 1) + 7} = (2k + 7) + 2
= {2 (k + 1) + 7}
Using Eq(1), we get
(2k + 7) + 2 < (k + 3)2 + 2
2 (k + 1) + 7 < k2 + 6k + 9 + 2
2 (k + 1) + 7 < k2 + 6k + 11
Here,
k2 + 6k + 11 < k2 + 8k + 16
2 (k + 1) + 7 < (k + 4)2
2 (k + 1) + 7 < {(k + 1) + 3}2
P (k + 1) is true whenever P (k) is true.
Therefore, by the principle of mathematical induction, statement P (n) is true for all natural numbers i.e. n.
Share your thoughts in the comments
Please Login to comment...