Parabola in Maths is one of conic sections i.e., it is an intersection of a surface plane and a double-napped cone. A parabola is a U-shaped curve that can be either concave up or down, depending on the equation. Parabolic curves are widely used in many fields such as physics, engineering, finance, and computer sciences.
The word “parabola” comes from the Greek word “παραβολή” (parabole), meaning “juxtaposition” or “comparison,” possibly referring to the two equal distances involved in its definition.
In this article, we will explore the parabolas from basic to advanced including topics like parabola form, formula, vertex, shape, and equation of parabola, etc.
What is Parabola in Maths?
A parabola is an equation of a specific curve, such that each point on the curve is always equidistant from a fixed point and a fixed-line. The fixed point is the parabola’s focus, and the fixed line is the directrix of the parabola. Therefore, in other words, the locus of a point that is equidistant from a given point (focus) and a given line (directrix) is called the parabola.
Parabola is one of the introductory curves in the study of conic section, as parabola and other conics can be obtained by slicing the double-napped cone (two identical cones stacked on top of each other from the vertex part) with the help of the surface plane at different angles.
Parabola Definition
Parabola is defined as the set of all points that are equidistant from a fixed point (called the focus) and a fixed straight line (called the directrix). The focus and directrix are two essential elements that determine the shape and position of a parabola.
Parabola Shape
A parabola is a U-shaped curved line where every point on the line is at an equal distance from the focus and directrix of the parabola.

Parabola Equation
The equation of a parabola can vary depending on its orientation and the position of its vertex, but one common form is:
y = ax2 + bx + c
Here, a, b, and c are constants. The shape of the parabola depends primarily on the value of a:
- If a>0, the parabola opens upwards.
- If a<0, the parabola opens downwards.
Properties of Parabola
- Axis of Symmetry: The line that is perpendicular to the directrix and passes through the focus is called the axis of symmetry. The parabola is symmetrical about its axis of symmetry.
- Vertex: The point where the parabola intersects its axis of symmetry is called the vertex. The vertex is the point where the parabola changes direction from opening upwards to opening downwards (or vice versa).
- Focal Length: The distance between the vertex and the focus is called the focal length. All parabolas with the same focal length are similar.
- Directrix: The fixed line from which any point on the parabola is the same distance as the focus.
- Reflective Property: If a parabola is made of a material that reflects light, then light that travels parallel to the axis of symmetry of a parabola and strikes its concave side is reflected to its focus, regardless of where on the parabola the reflection occurs. Conversely, light that originates from a point source at the focus is reflected into a parallel (“collimated”) beam, leaving the parabola parallel to the axis of symmetry.
- Equation: The equation of a parabola depends on its orientation and position. The standard equation of a parabola that opens upwards and is centered at the origin is y = x2. The standard equation of a parabola that opens downwards and is centered at the origin is y = -x2.
Parabola Examples
Parabolas are a common geometric shape found in various contexts, including mathematics, physics, engineering, and everyday life. Below are some real-world examples of Parabola:
- Projectile Motion: When an object is thrown or launched into the air, its path follows a parabolic trajectory under the influence of gravity. Examples include throwing a ball, shooting a cannonball, or launching a rocket.
- Satellite Dishes: The shape of satellite dishes is often parabolic. This design helps to focus incoming radio waves onto the receiver located at the focal point of the parabola.
- Headlights and Car Headlamp Reflectors: Many car headlights and headlamp reflectors use parabolic shapes to direct and focus light beams efficiently. The parabolic shape helps to project light in a specific direction, enhancing visibility for drivers.
- Solar Cookers: Parabolic solar cookers use a concave mirror in the shape of a parabola to focus sunlight onto a cooking vessel placed at the focal point. This concentrated solar energy can then be used for cooking food or heating water.
- Optical Telescopes: The primary mirrors of reflecting telescopes often have a parabolic shape. This shape helps to focus incoming light rays to form clear and sharp images of distant objects in space. The parabolic mirror collects and concentrates light from celestial objects, enabling astronomers to observe them with greater detail.
Standard Equation of Parabola
Standard Equation of Parabola is given as follows:
y2 = 4ax
In this form, directrix is parallel to the y-axis.
If directrix is parallel to the x-axis, then the standard equation of a parabola is given by,
x2 = 4ay
If the parabolas are drawn in alternate quadrants then their equation is given as y2 = -4ax and x2 = -4ay.
|
Form
|
y2 = 4ax
|
y2 = – 4ax
|
x2 = 4ay
|
x2 = – 4ay
|
| Vertex |
(0, 0)
|
(0,0)
|
(0, 0)
|
(0, 0)
|
| Focus |
(a, 0)
|
(-a, 0)
|
(0, a)
|
(0, -a)
|
| Equation of the axis |
y = 0
|
y = 0
|
x = 0
|
x = 0
|
| Equation of the directrix |
x = – a
|
x = a
|
y = – a
|
y = a
|
| Length of Latus rectum |
4a
|
4a
|
4a
|
4a
|

- Focus: Point (a, 0) is called the focus of a Standard Parabola (y2 = 4ax), and it has a very special property that has various real-life applications i.e. if any light ray traveling parallel to the axis of the parabola, the parabola converge those light rays at the focus.
- Directrix: A line drawn perpendicular to the base axis and passing through the point (-a, 0) is the directrix of the parabola. Directrix is always perpendicular to the axis of a parabola.
- Focal Chord: A chord passing through the focus of the parabola is called the focal chord of a parabola. The focal chord always cuts the parabola at two distinct points.
- Focal Distance: The distance of any point (x1,y1) lying on the parabola, from the focus of the parabola, is called the focal distance. The focal distance equals the perpendicular distance of the given point from the directrix.
- Latus Rectum: A chord perpendicular to the axis of the parabola and passing through the focus of the parabola is called the Latus rectum. Points at the ending of the latus rectum are (a, 2a), (a, -2a), and their length is taken as LL’ = 4a.
- Eccentricity: The ratio of the distance of a point from the focus, and the distance of the point from the directrix is called eccentricity. Eccentricity for a parabola is 1.
Parabola Equation Derivation
Take a point P with coordinates (x,y) on the parabola which lies on the X-Y plane. By the definition of the parabola, the distance of any point on the parabola from the focus and from the directrix is equal. Now distance of P from the directrix is given by PB where the coordinates of B are (-a, y) as it lies on the directrix, and the distance of P from focus is PF.
Image of parabola is shown below,

By the definition of parabola, PF = PB . . . .(1)
Using the Distance Formula, we get
PF = √(x−a)2+(y−0)2= √{(x−a)2+y2} . . . .(2)
PB = √{(x+a)2} . . . .(3)
By using, equations (1), (2), and (3), we get
√{(x−a)2+y2} = √{(x+a)2}
⇒ (x – a)2 + y2 = (x + a)2
⇒ x2 + a2 – 2ax + y2 = x2 + a2 + 2ax
⇒ y2 – 2ax = 2ax
y2 = 4ax
Which is the required equation of the parabola.
Similarly, the equation for other parabolas i.e., x2 = 4ay, y2 = -4ax, and x2 = -4ay, can also be proved.
Graph of Parabola
Graph of the parabola is a U-shaped curve, which can open either in an upward direction or in a downward direction. Generally, the equation of a parabola which is graphed is written in the form of y = ax2+bx+c, where a, b, and c are constants that define the shape of the parabola.
If a>0, in the above equation, the parabola opens in an upward direction and its vertex is the lowest point of the parabola, and if a<0, then the parabola opens in a downward direction and its vertex is the highest point in the parabola. The Vertex of the parabola is also the point from where the only line of symmetry of the parabola passes.
Position of a Point Relative to the Parabola
Position of a point A (x1, y1) relative to the parabola y2 = 4ax, can be shown using the S1 = y2 – 4ax,
Case 1: If S1 = 0, for any point A, then Point A lies on the parabola.
Case 2: If S1 < 0, for any point A, then Point A lies inside the parabola,
Case 3: If S1 > 0, for any point A, then Point A lies outside the parabola.
Intersection with Straight Line
For a parabola y2 = 4ax, any straight line y = mx + c, can almost intersect the parabola at two points. For the intersection of the line and parabola, put y = mx + c in the equation of the parabola,
the mx + c)2 = 4ax
⇒ m2x2 + c2 + 2mxc = 4ax
⇒ m2x2 + (2mc – 4a)x + c2= 0
⇒ Discriminant = (2mc – 4a)2 – 4m2c2
Case 1: Discriminant > 0:
For positive discriminant, quadratic equations have two real solution,
⇒ There are two point of intersection between line and parabola.
Case 2: Discriminant = 0:
For discriminant equal to 0, quadratic equations have only real solution (common root),
⇒ There are open point of intersection between line and parabola i.e., line is tangent to parabola.
Case 3: Discriminant < 0:
For negative discriminant, quadratic equations have no real roots.
⇒ There are no point of intersection between line and parabola.
General Equations of Parabola
The General equation of a parabola is given by y = a(x – h)2 + k or x = a(y – k)2 +h where (h, k) denotes the vertex of the parabola.
(Regular form) y = a(x – h)2 + k
(Sidewise from) x = a(y – k)2 +h
Parametric Coordinates of a Parabola
For a parabola, y2 = 4ax, if we take x = at2 and y = 2at for any value of “t” they will satisfy the equation of a parabola, the coordinates (at2, 2at) is termed as parametric coordinate, and “t” is called as the parameter.
Thus, x = at2 and y = 2at are called the parametric equations of the parabola y2 = 4ax
Similarly, parametric form of the parabola x2 = 4ay are x = 2at, y = at2
Equation of Tangent to a Parabola
Tangents are lines that touch the curve only at a single point. So a line that touches the parabola exactly at one single point is called the tangent to a parabola.
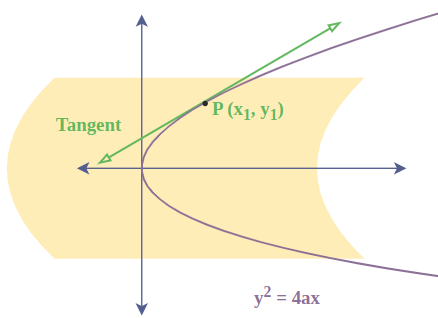
There are various ways to find the tangent of a parabola which are discussed in next sections.
Equation of Tangent in Point Form
For the given parabola y2 = 4ax equation of the tangent at point (x1, y1) is given by:
yy1 = 2a(x+x1)
where,
(x1, y1) is the point of contact between the tangent and the curve.
Equation of Tangent in Parametric Form
For the given parabola y2 = 4ax equation of the tangent at point (at2, 2at) is given by:
ty = x + at2
where,
(at2, 2at) is the point of contact between the tangent and the curve.
Equation of Tangent in Slope Form
For the given parabola y2 = 4ax with slope m equation of the tangent at point (a/m2, 2a/m) is given by
y = mx + a/m
where,
(a/m2, 2a/m) is the point of contact between the tangent and the curve.
Pair of Tangent from an External Point
Pair of tangents from an external point to any conic is given by SS1 = T2
where for parabola y2 = 4ax, S = y2 – 4ax, S1 = y12 -4ax1 and T = yy1 – 2a(x + x1).
Thus, the equation of pair of tangents from an external point becomes:
(y2 – 4ax)( y12 -4ax1) = [yy1 – 2a(x + x1)]2
Director Circle of Parabola
Director circle is the geometric object related to the conic section and is defined as the locus of the intersection of the pair perpendicular tangent of any conic. For the parabola, the director circle is the directrix as all the perpendicular pairs of tangents of the parabola intersect each other at the directrix.

Chord of Contact
Chord of contact of the parabola is a secant line joining the point of tangency for the tangents drawn from the external point on the parabola. For parabola y2 = 4ax, chord of contact is given by T = 0, where T = yy1 – 2a(x + x1).Therefore the equation of chord of contact is given
T = yy1 – 2a(x + x1) =0
Where, (x1, y1) is the external point from which both the tangents are drawn to the parabola.

Equation of Normal to a Parabola
A line perpendicular to the tangent of the parabola at the point of tangency is known as the normal of the parabola. As this line is perpendicular to the tangent at the point of tangency to the parabola, the equation of this line can be found easily if the equation of tangent and point of tangency is given, using the concept of the equation of line perpendicular to the given line, but this is not always the case.

The equation of normal is given in three ways as follows:
Equation of Normal in Slope Form
For a parabola y2 = 4ax and m is the slope of normal at the point of contact (am2, -2am), the equation of normal is given by:
y = mx – 2am – am3
Equation of Normal in Point Form
For a parabola y2 = 4ax, equation of normal at (x1, y1) is given as follows:
y – y1 = (-y1/2a)(x – x1)
Equation of Normal in Parametric Form
For a parabola y2 = 4ax, the equation of normal at the point (at2, 2at) [where t is the parameter] is given as follows:
y = -tx + 2at + at3
| Formula/Property |
Equation or Description |
| Standard Equation of Parabola |
y2 = 4ax (or x2 = 4ay for a different orientation) |
| Focus |
(a, 0) for y2 = 4ax (or (0, a) for x2 = 4ay) |
| Directrix |
x = -a for y2 = 4ax (or y = -a for x2 = 4ay) |
| Latus Rectum |
4a |
| Eccentricity |
1 |
| General Equations of Parabola |
y = a(x – h)2 + k OR x = a(y – k)2 +h |
| Parametric Equation of Parabola |
x = 2at, y = at2 |
| Equation of Tangent |
yy1 = 2a(x + x1) |
| Equation of Tangent in Parametric Form |
ty = x + at2 [where, (at2, 2at) is the point of contact] |
| Equation of Tangent in Slope Form |
y = mx + a/m [Where m is the slope of Tangent] |
| Pair of Tangent from an External Point |
(y2 – 4ax)( y12 -4ax1) = [yy1 – 2a(x + x1)]2 |
| Director Circle |
Directrix i.e., x = -a [For y2 = 4ax] |
| Chord of Contact |
yy1 – 2a(x + x1) =0 |
| Equation of Normal in Slope Form |
y = mx – 2am – am3 |
| Equation of Normal in Normal Form |
y – y1 = (-y1/2a)(x – x1) |
| Equation of Normal in Parametric Form |
y = -tx + 2at + at3 |
Applications of Parabola in Real Life
1. Architecture and Structural Engineering
Parabolic shapes are valued in architecture for their aesthetic appeal and structural advantages. The arches of bridges, vaults in cathedrals, and roofs of modern buildings often employ parabolic designs because they can distribute weight very efficiently. This natural strength enables structures to withstand heavy loads while using less material.
2. Headlights and Satellite Dishes
In the realm of optics, the parabolic shape is crucial. The reflective properties of a parabola mean that light rays entering a parabolic mirror parallel to its axis will reflect and focus at a single point. This principle is used in car headlights to direct light into a beam that illuminates the road ahead. Similarly, satellite dishes use parabolic reflectors to focus radio waves from space onto a central receiver, enhancing signal strength.
3. Sports
You’ll see parabolas in action in many sports where objects are thrown or propelled. For example, a basketball arcing towards the hoop, a soccer ball kicked in a lob pass, or a diver jumping off a high dive all follow parabolic trajectories under the influence of gravity and initial force. Understanding these paths can help athletes improve their technique to achieve better control over their movements.
4. Water Fountains
The mesmerizing arcs of water in ornamental fountains are examples of parabolas. The path of each water droplet traces a parabolic curve, shaped by the force of the pump and the pull of gravity. Fountain designers can use this knowledge to predict where water will land, avoiding unwanted splashing and creating beautiful, symmetrical water displays.
5. Physics and Astronomy
Parabolas are also significant in physics, particularly in the study of motion and celestial mechanics. Objects in freefall near the Earth’s surface follow a parabolic path when air resistance is negligible. Additionally, parabolic trajectories are crucial in understanding the orbits of comets around the sun, which often bring them into the inner solar system before swinging back out into space.
6. Entertainment Industry
In the world of entertainment, particularly in stage productions and films, parabolic microphones are used to capture sound. These microphones use a parabolic reflector to focus sound waves from a wide area onto a single point where the microphone is placed, allowing clear audio pickup from distant sources.
People Also View:
Parabola Solved Examples
Question 1: Find coordinates of the focus, axis, the equation of the directrix, and latus rectum of the parabola y2 = 16x.
Solution:
Given equation of the parabola is: y2 = 16x
Comparing with the standard form y2 = 4ax,
4a = 16 ⇒ a = 4
The coefficient of x is positive so the parabola opens to the right.
Also, the axis of symmetry is along the positive x-axis.
Therefore,
Focus of the parabola is (a, 0) = (4, 0).
Equation of the directrix is x = -a, i.e. x = -4
Length of the latus rectum = 4a = 4(4) = 16
Question 2: Find the equation of the parabola which is symmetric about the y-axis, and passes through the point (3, -4).
Solution:
Given that parabola is symmetric about the y-axis and has its vertex at the origin.
Thus, equation can be of the form x2 = 4ay or x2 = -4ay, where the sign depends on whether the parabola opens upwards or downwards.
Since parabola passes through (3, -4) which lies in the fourth quadrant, it must open downwards.
So, equation will be: x2 = -4ay
Substituting (3, -4) in the above equation,
(3)2 = -4a(-4)
9 = 16a
a = 9/16
Hence, the equation of the parabola is: x2 = -4(9/16)y
4x2 = -9y
Question 3: Find coordinates of the focus, axis, and the equation of the directrix and latus rectum of the parabola y2 = 8x.
Solution:
Given equation of the parabola is: y2 = 8x
Comparing with the standard form y2 = 4ax,
4a = 8
a = 2
The coefficient of x is positive so the parabola opens to the right.
Also, the axis of symmetry is along the positive x-axis.
Therefore,
Focus of the parabola is (a, 0) = (2, 0).
Equation of the directrix is x = -a, i.e. x = -2
Length of the latus rectum = 4a = 4(2) = 8
Question 4: Find the coordinates of the focus, axis, the equation of the directrix, and latus rectum of the parabola y2 = 52x.
Solution:
Given equation of parabola is: y2 = 52x
Comparing with the standard form y2 = 4ax,
4a = 52
a = 13
The coefficient of x is positive so the parabola opens to the right.
Also, the axis of symmetry is along the positive x-axis.
Therefore,
Focus of the parabola is (a, 0) = (13, 0).
Equation of the directrix is x = -a, i.e. x = -13
Length of the latus rectum = 4a = 4(13) = 52
Question 5: Find coordinates of the focus, axis, the equation of the directrix, and latus rectum of the parabola x2 = 16y.
Solution:
Given equation of parabola is: x2 = 16y
Comparing with standard form x2 = 4ay,
4a = 16
a = 4
The coefficient of x is positive so the parabola opens upward.
Also, the axis of symmetry is along the positive x-axis.
Therefore,
Focus of the parabola is (0,a) = (0, 4).
Equation of the directrix is y= -a, i.e. y = -4
Length of the latus rectum = 4a = 4(4) = 16
Parabola Worksheet
1. Find the vertex, focus, and directrix of the parabola with the equation y = x2 − 4x + 3y = x2 − 4x + 3.
2. Determine whether the parabola with the equation y = −2x2 + 4x − 1y = −2x2+4x−1 opens upward or downward, and find its vertex.
3. Given the equation 4x2 − 16y=0, 4x2 − 16y=0, rewrite it in standard form and find the vertex, focus, and directrix of the parabola.
4. Solve for xx in the equation 2x2 − 3x − 5 = 0, 2x2 − 3x − 5 = 0, and determine the nature of the roots with respect to the corresponding parabola.
Parabola MCQs Practice Problems
To learn more about Parabola Practice MCQs on Parabola
FAQs on Parabola
What is Parabola in Maths?
Parabola is the set of all points that are equidistant from a fixed point (called the focus) and a fixed straight line (called the directrix).
What is meant by Conjugate Axis of a Parabola?
A line that passes through the vertex of the parabola and is perpendicular to its transverse axis is called the conjugate axis of the parabola.
What are Real-life applications of Parabola?
Parabolas are used for a variety of purposes some of them are
- Parabolic arch is used in the construction of various monuments.
- Parabolic mirrors are used in reflecting telescopes, satellites, etc.
- Parabolas are used in various mathematical calculations, such as tracing the path of a missile, the trajectory of a bullet, etc.
What is Shape of a Parabola?
Graph of a parabola is in the shape of U.
What is Eccentricity of a Parabola?
Eccentricity is defined as the ratio of distances of any point of conic section to its focus and corresponding directrix. For parabola eccentricity is 1.
What is Formula for Length of Latus Rectum of a Parabola?
For parabola y2 = 4ax, length of the latus rectum is calculated by 4a..
What is Vertex of a Parabola?
The point of intersection of the parabola and both the conjugate axis is called the vertex of a parabola. If the equation of parabola is y2 = 4ax, then the vertex is (0, 0).
What is a Parabolic motion?
Parabola motion, also known as projectile motion, describes the path followed by an object that is subject only to the force of gravity and no other external forces, such as air resistance. In this type of motion, the object moves in a curved path that resembles a parabola.
What are 4 Types of Parabola?
Parabolas can generally be categorized into four types based on their orientation and direction:
- Vertical Opening Up: The standard form is y=ax2+bx+c, where a > 0.
- Vertical Opening Down: The standard form is y=ax2+bx+c, where a < 0.
- Horizontal Opening Right: The standard form is x=ay2+by+c, where a > 0.
- Horizontal Opening Left: The standard form is x=ay2+by+c, where a < 0.
What is a Parabola vs Hyperbola?
A parabola is a U-shaped curve where any point is at an equal distance from a fixed point (the focus) and a fixed straight line (the directrix). It has one axis of symmetry.
A hyperbola is a curve where the difference of the distances from two points (the foci) is constant. It has two disconnected parts and two axes of symmetry.
What are 4 key Features of a Parabola?
- Vertex: The highest or lowest point of the parabola.
- Axis of Symmetry: The line that divides the parabola into two symmetric halves.
- Focus: A fixed point through which all the parallel light rays reflect off a parabolic mirror.
- Directrix: A fixed line that is equidistant from all points on the parabola.
How to solve Parabola?
Solving a parabola involves various tasks such as finding its vertex, axis of symmetry, intercepts, and sometimes roots (solutions to quadratic equations). You can solve a parabola by using algebraic methods, completing the square, factoring, quadratic formula, or graphical methods.
Who invented Parabola?
Concept of the parabola and its mathematical properties have been studied and developed over centuries by various mathematicians and scholars. However, it was the ancient Greek mathematician Apollonius of Perga who extensively studied conic sections, including the parabola, around the 3rd century BCE.
What are the 3 parts of Parabola?
Three main parts of a parabola are:
- Vertex: The highest or lowest point of the parabola, where the curve changes direction.
- Axis of Symmetry: The line that divides the parabola into two symmetric halves.
- Focus: A fixed point inside the parabola, which is equidistant from all points on the parabola.
Share your thoughts in the comments
Please Login to comment...