Linear Graphs as the name suggests, are graphs with linear relationships between both variables. In the case of any two variables, the relation between these two variables can be drawn by constructing the table of values if the rule for that relation is mentioned. At least two points coordinates should be known to plot a straight-line graph. These points must fit the rule and such graphs when drawn are termed Linear graphs.
Linear Graphs Definition
A line graph with continuous or unbroken nature is called a linear graph.
To draw the unbroken line we need to locate some points on the graph sheet. Let’s make a graph with an x and y-coordinate.
Suppose you go to an auditorium and search for your reserved seat. You need to know two numbers, the row number, and the seat number. This is the basic method for fixing a point in a plane.
Linear Graph Equation
All the linear graphs can be represented by the linear equation in two variables, such that
y = mx + c
Where,
- x and y are variables that we represent on the x and y-axis,
- m is the slope of the graph, and
- c is the y-intercept of the graph.
Note: This equation is called the slope-intercept form of the linear.
Standard Form of Linear Equation
The standard form of the linear equation is given as follows:
Ax + By + C = 0
Where,
- x and y are variables that we represent on the x and y-axis,
- A, B, and C are the real constant.
How To Plot Linear Equation On a Graph?
For a general linear equation in the form Ax + By = C, you can plot the Linear Equation On a Graph using the following steps:
Step 1: Rearrange the given equation to find the value of y.
By = C – Ax
y = (-A/B)x + C/B
Step 2: Put x = 0, to find Y-intercept of the graph i.e., point of intersectino between line and y-axis and mark the point in the graph.
y = C/B
Thus, y-intercept is (0, C/B).
Step 3: Put y = 0, to find X-intercept of the graph i.e., point of intersectino between line and x-axis mark the point in the graph.
0 = (-A/B)x + C/B
x = C/A
Thus, x-intercept is (C/A, 0)
Step 4: Meet the both intercepts to plot the Linear Equation On a Graph.
Linear Graph vs Line Graph
A linear Graph is an unbroken line with the same slope throughout the line and always can be represented by a linear equation.
Whereas, a line graph is a collection of line segments with each starting from where the last one is ending, and all line segments have various slopes. Also, these different line segments can’t be represented by a single linear equation.
Application of Linear Graphs
In everyday life, we observe variations in the value of different quantities, or we can say that the more we use the facility the more we have to pay for it. for e.g. If more electricity we consume we will have to pay the bill more and vice versa. So one quantity affects the other quantity. We can say that the quantity of electricity is the independent variable and the amount of bills is the dependent variable. These relations we can show with graphs.
Read More,
Sample Problems on Linear Graphs
Problem 1: Plot (3, 4) on the graph
Solution:
As in graph points are denoted in the form of (x, y)
So, on comparing the points:
x = 3 and y = 4.
First, draw x = 3 moves in the forward direction to x = 3.
Now, draw y = 4 moves in the upward direction to (3, 4).
Problem 2: Locate the given points on the graph.
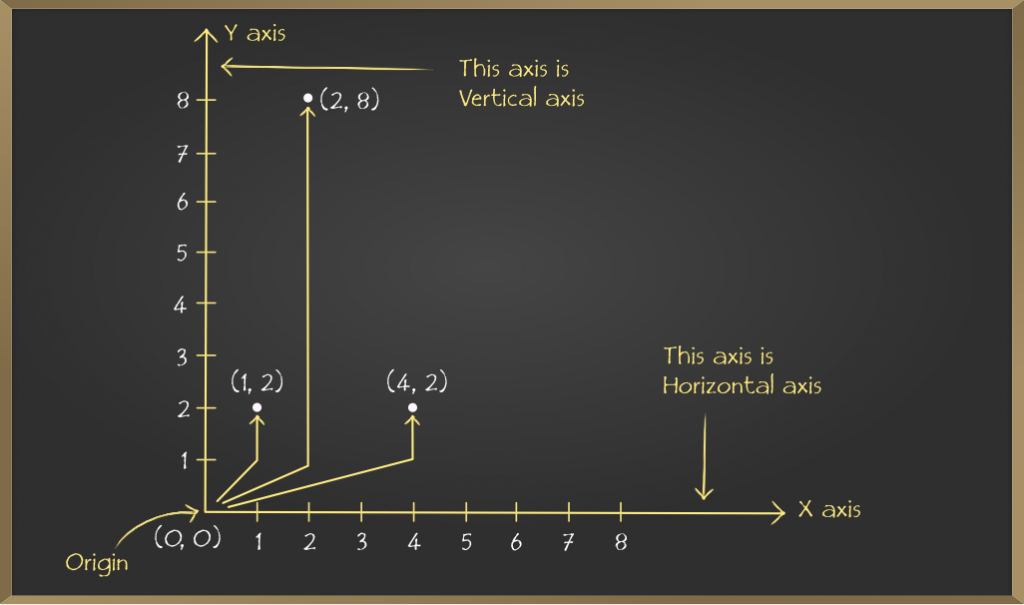
- (1, 2)
- (2, 8)
- (4, 2)
Solution:
For x = 1 and y = 2. Starting from (0, 0) origin we move x = 1 direction forward and from there we move y = 2 direction upward then finally reaching state is our point.
Similarly, plot the rest of the two points on Graph.
Problem 3: Plot the following points and verify if they lie on the line.
- (0, 1), (0, 2), (0, 4), (0, 3)
- (1, 1), (2, 2), (3, 3), (4, 4), (5, 5)
Solution:
1. Plotting (0, 1), (0, 2), (0, 4), (0, 3) on graph
We can draw every coordinate on graph sheet as follows .
Here it forms a line after joining all the points.
2. Plotting (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) on graph
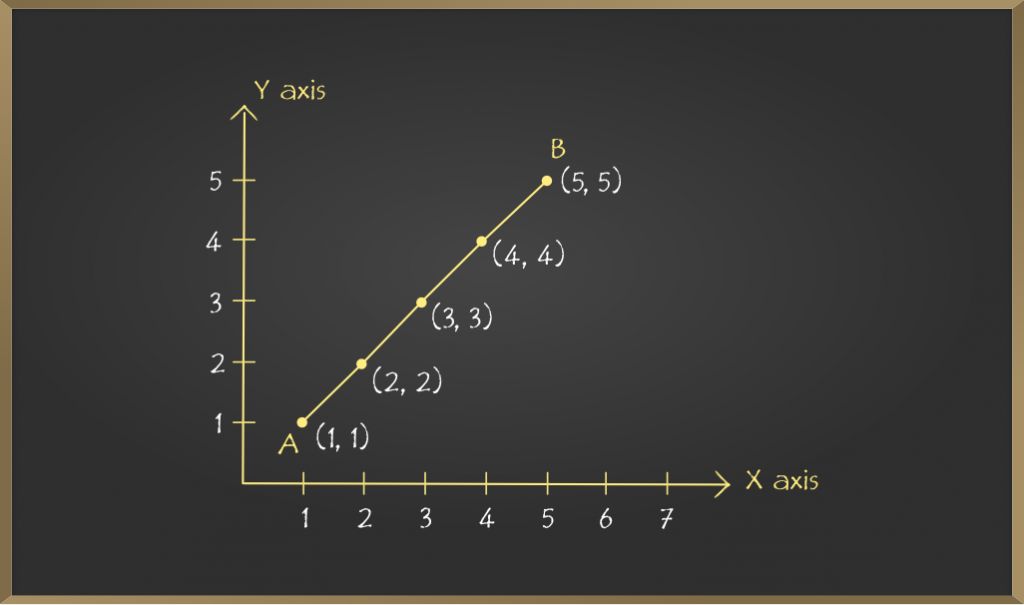
Note: In each of the above cases, the graph obtained by joining the plotted points is a line. Such graphs are called linear graphs.
Problem 4: Amit can ride a bike at a constant speed of 30 km/hour. Draw a time-distance graph for this situation and find it
(i) Time is taken by Amit to ride 75 km.
(ii) Distance covered by Amit in 3.5 hours.
Solution:
| Hours of ride | Distance covered |
1 hour 2 hours 3 hours 4 hours | 30 km 2Ă—30 = 60km 3Ă—30 = 90km 4Ă—30 =120km |
The table so formed is:
| Time (in hours) | 1 | 2 | 3 | 4 |
| Distance covered (in km) | 30 | 60 | 90 | 120 |
Consider the Scale:
Horizontal: 2 units = 1 hour
Vertical: 1 unit = 10 km
Mark time on horizontal axis.
Mark distance on vertical axis
Plot points: (1, 30), (2, 60), (3, 90), (4, 120)
On joining the points the required linear graph is obtained.
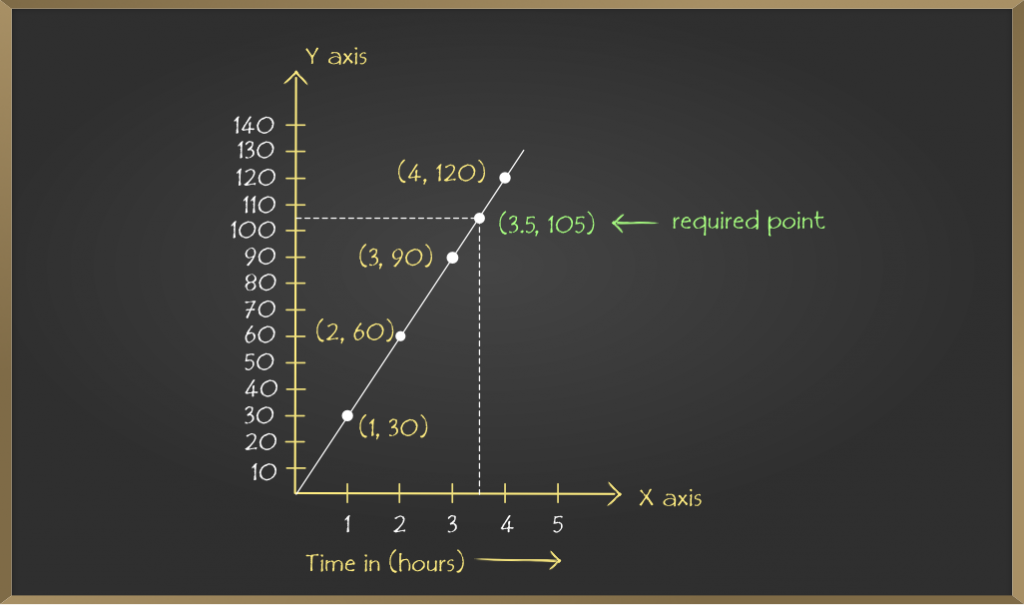
(i) From the above graph it is concluded that on the vertical axis corresponding to the distance 75 km, the time is 2.5 hours on the horizontal axis. Thus, 2.5 hours are needed to cover 75 km.
(ii) Similarly, on the horizontal axis corresponding to time 3.5 hours, the distance covered is 105 km on the vertical axis.
Problem 5: A public bank provides 10% interest on deposits by senior citizens. Plot a graph representing the relation between the deposited amount and the interest earned by senior citizens and state the following things from the graph so plotted:
(i) The interest earned annually for an investment of â‚ą 450.
(ii) The amount of money deposited to earn the interest of â‚ą 35.
| Amount deposited (in â‚ą) | 100 | 300 | 500 | 700 | 900 |
|---|
| Interest earned (in â‚ą) | 10 | 30 | 50 | 70 | 90 |
|---|
Solution:
Consider the Scale:
Horizontal: 1 unit = â‚ą 10
Vertical: 1 unit = â‚ą 100
Mark interest earned on horizontal axis.
Mark amount deposited on vertical axis.
Plot the points: (10, 100), (30, 300), (50, 500), (70, 700) and (90, 900) on the graph.
On joining the points the required linear graph is obtained.
(i) From the above graph it is concluded that on the vertical axis corresponding to the amount deposited â‚ą 450, the interest earned is â‚ą 45 on the horizontal axis. Thus, â‚ą 45 are earned on the deposit of â‚ą 450.
(ii) Similarly, on the horizontal axis corresponding to interest earned 35%, the amount deposited is â‚ą 350 on the vertical axis.
FAQs on Linear Graphs
Q1: What is a Linear Graph?
Answer:
A linear graph is a continuous graph in the shape of a line that can be infinitely increased to both sides similar to a line.
Q2: What is the Slope of a Linear Graph?
Answer:
Change in the y-coordinate with respect to the x-coordinate is called slope of a linear graph. Mathematically it can be represented as
Slope = Δy/Δx
Where,
- Δy represents the change in y-coordinate, and
- Δx represnts the change in x-coordinate.
Q3: How to Graph a Linear Equation?
Answer:
To graph any linear equation, we can find two points that satisfy the equation and meet that two points to form a line that represents all the points satisfying the linear equation.
Q4: What is the X-Intercept of a Linear Graph?
Answer:
The point where the linear graph cuts the x-axis, is called the x-intercept.
Q5: What is the Y-Intercept of a Linear Graph?
Answer:
The point where the linear graph cuts the y-axis, is called the y-intercept.
Q6: What is the Point-Slope form of a Linear Equation?
Answer:
The Point-slope form of the linear equation is given by
y – y1 = m(x – x1)
Where,
- x and y are variables that we represent on the x and y-axis,
- m is the slope of the graph, and
- x1 and y1 are the coordinate of the point from where line passes through.
Q7: What is the Standard Form of a Linear Equation?
Answer:
The standard form of the linear equation is given as follows:
Ax + By + C = 0
Where,
- x and y are variables that we represent on the x and y-axis,
- A, B, and C are the real constant.