Kite – Quadrilaterals
Last Updated :
21 Mar, 2024
A Kite is a quadrilateral in which four sides can be grouped into two pairs of equal-length sides that are adjacent to each other and the diagonals intersect each other at right angles. It is one of the unique quadrilateral and has some interesting properties that are covered below in the article. In this article, we will learn about, Kite Quadrilateral, Properties of Kite, Examples, and others, in detail.
What is a Kite?
Kite is a quadrilateral, i.e. it is a polygon with four sides. In a kite, we have 2 pairs of equal-length sides and they are adjacent to each other. The image of a Kite is added below,

Properties of Kite
Various properties of the kite are added below,
- Kite has 2 diagonals that intersect each other at right angles.
- A kite is symmetrical about its main diagonal.
- Angles opposite to the main diagonal are equal.
- The kite can be viewed as a pair of congruent triangles with a common base.
- The shorter diagonal divides the kite into 2 isosceles triangles.
- The area of the kite is 1/2 × d1 × d2
Diagonals of a Kite
A kite have two diagonals, and the properties of the diagonls of the kite are added below,
- Diagonals of the kite are not equal.
- Digonal of kite are perpendicular to each other, they intersect each other right angles.
- Shorter diagonal of a kite forms two Iscosceles Triangles.
- Longer diagonal of a kite forms two congruent triangle by SSS property of Congruence.
Theorem: Diagonals of Kite Intersect at Right Angles
The interesting properties of the kite is that its diagonal are always perpendicular to each other. This is proved below, we have a kite ABCD, whose diagonal intersect each other at point O.
In ∆ABD and ∆BCD
AB = BC (Property of Kite)
AD = CD (Property of Kite)
BD = BD (Common Side)
Thus, ∆ABD ≅ ∆BCD (SSS congruency)
Now, in ∆ABC and ∆ADC
AB = BC (Property of Kite)
Hence ∆ABC is an isosceles triangle.
AD = CD (Property of Kite)
Hence ∆ADC is an isosceles triangle.
∠BAO = ∠BCO
BO = BO (Common Side)
Thus, ∆ABO ≅ ∆BCO (SAS rule of congruency)
Now we know ∠AOB = ∠BOC
Also, ∠AOB + ∠BOC = 180° (Linear Pair)
Hence, ∠AOB = ∠BOC = 90°
Hence diagonals of kite intersect at right angles.
Angles in a Kite
In a kite we have four angles, as it a quadrilateral. The properties of the interior angles of the kite are,
- The sum of all the angle of the kite is 360°.
- Any one pair of angles in kite (obtuse angle pair) are equal.
Area of Kite
Area of Kite is calculated by the formula for area of quadrilateral. Generally Area of Kite is calculated by the formula added below,
Area of Kite = 1/2 × d1 × d2
where,
- d1 is Shorter Diagonal of Kite
- d2 is Longer Diagonal of Kite
Perimeter of Kite
Perimeter of Kite is calculated by adding up the length of sides of the kite. If a Kite ABCD is given then formula is given as
Perimeter of Kite ABCD = AB + BC + CD + AD
Read More,
Solved Examples on Kite
Example 1: Find the Area of a Kite whose diagonals are 40 cm and 35 cm.
Solution:
Area of Kite with diagonals as d1 and d2 is given as 1/2 × d1 × d2
Given,
Area = 1/2 × 40 × 35
Area = 700 cm2
Hence, the area of kite is 700 cm2
Example 2: Find the unknown angles of the kite added in the image below,
Given,
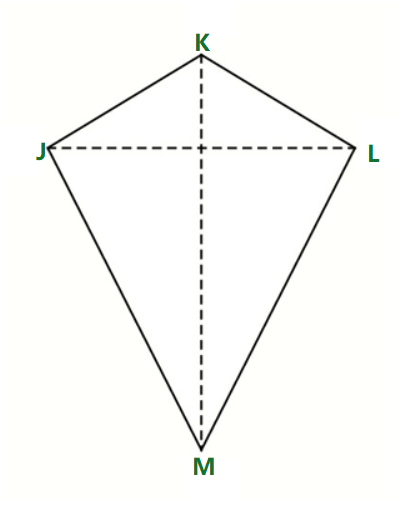
Solution:
We know that, main diagonal bisects the kite into two halves.
Thus,
∠KJL = ∠KLM
Hence ∠KLM = ∠KJL = 100° (given)
Sum of all angles of quadrilateral is 360°
Thus,
∠JML = 120°
Example 3: The Area of a kite-shaped field is 450 m² and the length of one of its diagonal is 50 m. A man wants to cross the field through the other diagonal. Find the distance the man has to travel.
Solution:
Given,
- Area of Kite = 450 m2
- Length of One Diagonal(d1) = 50 m
Let the other diagonal of kite is d2
Area of Kite = 1/2 × d1 × d2
450 = 1/2 × 50 × d2
d2 = 18 m
Hence, other man has to travel a distance of 18 m.
Practice Questions on Kite
Q1. Find the area of kite whose one diagonal is 12 cm and other diagonal is 30 cm.
Q2. In a kite whose sides are, 5 cm and 8 cm. Find its perimeter.
Q3. Find the area of kite whose one diagonal is 7 cm and other diagonal is 3 cm.
Q4. In a kite with sides, 21 cm and 23 cm. Find its perimeter.
Kites – FAQs
1. What is Kite in Geometry?
Kite in a geometry is a quadrilateral in which pair of adjacent sides are equal .
2. What are Examples of Kite Shape?
Various types of examples representing the kite shape is,
- Kite Toy
- Kite shaped Jwellery
- Kite shaped sweets
- Kite shaped traffic sign, etc
3. What Area of Kite Formula?
The area of kite is given by the formula,
Area of Kite = 1/2 × d1 × d2
where,
- d1 is Shorter Diagonal of Kite
- d2 is Longer Diagonal of Kite
4. What are Properties of Kite?
Various properties of the kite are,
- Two pairs of adjacent sides are equal in kite.
- One pair of opposite angles are equal in a kite.
- Diagonals of a kite are perpendicular to each other, etc.
5. What is the Sum of All Angles of Kite?
Sum of all the angles of the kite is 360° it is a quadrilateral and some of all the angles of quadrilateral is 360°.
Share your thoughts in the comments
Please Login to comment...