Area of triangle is the region enclosed by all its three sides. It is generally calculated with the help of its base and height.
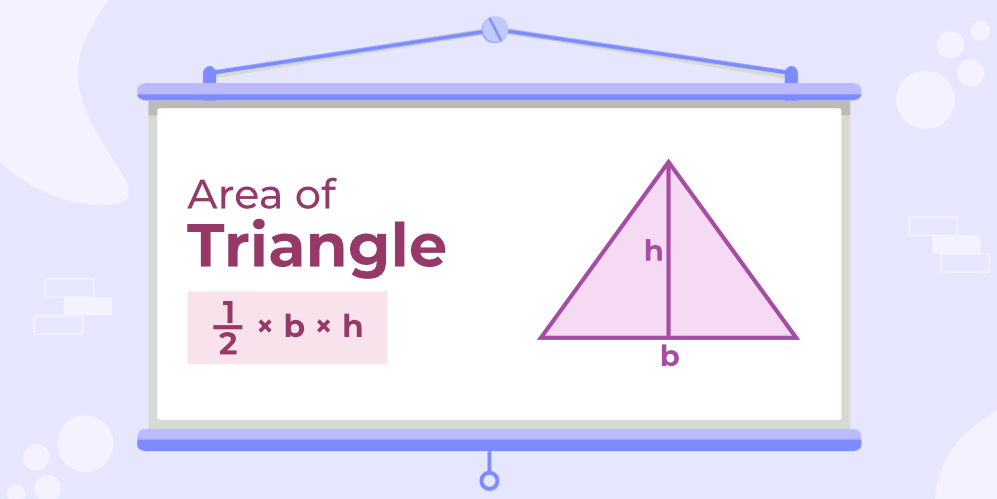
Let’s learn about the area formulas for different types triangles in detail, with the help of solved examples.
What is Area of Triangle?
Area of triangle is defined as the total surface enclosed by the boundaries of the triangle. It is measured in square units i.e. m2, cm2, etc.
The most general triangle formula for area is given by half the product of its base and height. It applies to all types of triangles, whether it is equilateral , isosceles, or scalene triangle.
Area of Triangle Formula
Formula of area of triangle depends on the dimensions of the triangle. The following table consists of the area of triangle formulas used in different contexts :
|
| Right-Angled Triangle |
½ × base × height |
| Equilateral Triangle | (√3)/4 × side2 |
| Isosceles Triangle | ¼ × b√(4a2 – b2) |
| Using Heron’s Formula | √{s(s-a)(s-b)(s-c)}
,where s = ½ (a+b+c) |
| When Two Sides and Included Angle (SAS) are given | ½ × side 1 × side 2 × sin(θ)
, where θ is the angle between the given two sides
|
| In Coordinate Geometry | ½ |x1(y2 – y3 ) + x2(y3 – y1) + x3(y1 – y2)|
, where (x1, y1), (x2, y2) and (x3, y3) are the coordinates of triangle. |
Let’s discuss them in detail.
Area of Right Angled Triangle
A triangle that contains a right angle is considered a right-angled triangle.

Area of Right Angled Triangle Formula :
A = 1/2 × a × c
where,
a is base of the triangle
c is height of the triangle
Read More :
Area of Equilateral Triangle
An equilateral triangle has all three sides equal and all three angles equal, measuring 60 degrees.

Area of Equilateral Triangle Formula :
A = (√3)/4 × side2
= (√3)/4 × a2
Read More :
Area of Isosceles Triangle
An isosceles triangle has two equal sides and the angles opposite these equal sides are also equal.

Area of Isosceles Triangle Formula :
A = ¼ × b√(4a2 – b2)
where, a = both the equal sides
and b= the third unequal side
Learn More :
Area of Triangle By Heron’s Formula
Area of triangle with 3 sides given can be found using Heron’s Formula. This formula is useful when the height is not given.
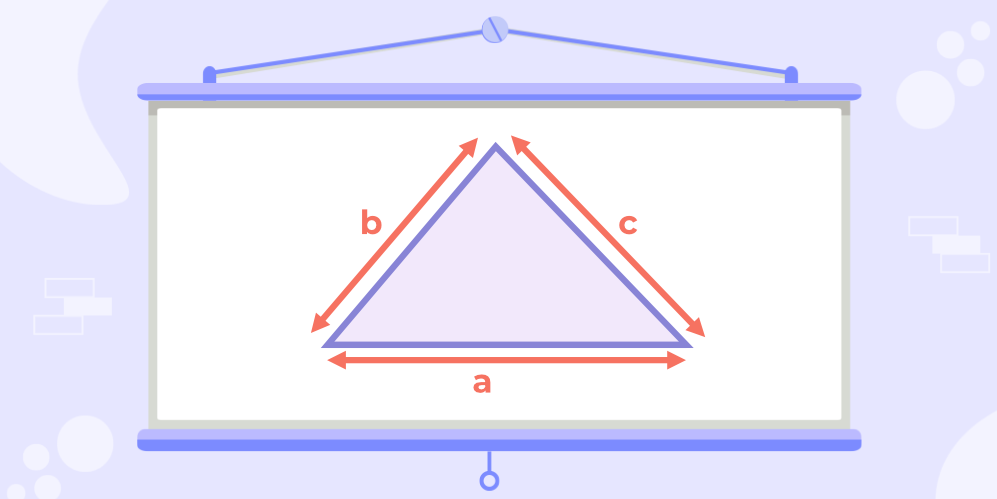
Heron’s Formula is given by,
Area of Triangle = √{s(s-a)(s-b)(s-c)}
where, a, b, and c are sides of the given triangle
and s = ½ (a+b+c) is the semiperimeter.
Example: What is the area of triangle with sides of 3 cm, 4 cm, and 5 cm?
Solution:
Using Heron’s formula,
s = (a+b+c)/2
= (3+4+5)/2
= 12/2 = 6
Area = √{ s(s-a)(s-b)(s-c)}
= √{ 6(6-3)(6-4)(6-5)}
= √(6 × 3 × 2 × 1) = √(36)
= 6 cm2
Learn More :
Area of Triangle With Two Sides and Included Angle (SAS)
Formula for the Area Of SAS Triangle is obtained by using the concept of trigonometry.
Let us assume ABC is right angled triangle and AD is perpendicular to BC.

In the above figure,
Sin B = AD/AB
⇒ AD = AB Sin B = c Sin B
⇒ Area of Triangle ABC = 1/2 ⨯ Base ⨯ Height
⇒ Area of Triangle ABC = 1/2 ⨯ BC ⨯ AD
⇒ Area of Triangle ABC = 1/2 ⨯ a ⨯ c Sin B
= 1/2 ⨯ BC ⨯ AD
Thus,
Area of Triangle = 1/2 ac Sin B
Similarly, we can find that ,
Area of Triangle = 1/2 bc Sin A
Area of Triangle = 1/2 ab Sin C
We conclude that the area of triangle using trigonometry is given as the half the product of two sides and sine of the included angle.
In Coordinate Geometry, if the coordinates of triangle ABC are given as A(x1, y1), B(x2, y2) and C(x3, y3), then its Area is given by the following formula :
Area of △ABC = 1/2
⇒ Area of △ABC = 1/2 |x1(y2 – y3 ) + x2(y3 – y1) + x3(y1 – y2)|
Related Article :
Solved Examples on Area of Triangle
Let’s solve some example problems on Area of Triangle.
Example 1: What is the area of triangle with sides of 8 cm, 6 cm, and 10 cm (using Heron’s Formula)?
Solution:
Using Heron’s formula,
s = (a+b+c)/2
= (8+6+10)/2
= 24/2 = 12
Area = √{ s(s-a)(s-b)(s-c)}
= √{ 12(12-8)(12-6)(12-10)}
= √(12×4×6×2) = √(576)
= 24 cm2
Example 2: Find the area of a right-angled triangle having base a = 5 cm and height c = 3 cm.
Solution:
Given
Base of the triangle (a) = 5 cm
Height of the triangle (c) = 3 cm
We have,
Area(A) = 1/2 × a × c
= 1/2 × 5 × 3
= 7.5 cm2
Example 3: Find the area of an equilateral triangle having side a = 6 cm
Solution:
Given,
side of the triangle (a) = 6 cm
Area(A) = (√3)/4 × a2
= (√3)/4 × 62
= 9√3 cm2
Practice Problems on Area of Triangle
Here is a worksheet on Area of Triangle for you to solve.
1. Find the area of triangle with a base of 8 inches and a height of 5 inches.
2. Calculate the area of an equilateral triangle with a side length of 6 centimeters.
3. Given a right triangle with one leg measuring 10 meters and the other leg measuring 24 meters, what is the area of triangle?
4. Determine the area of an isosceles triangle with a base of 12 feet and each of the congruent sides measuring 9 feet.
How To Find Area of Triangle- FAQs
1. What is Area of triangle?
The region enclosed by the boundary of the triangle i.e. area occupied by the perimeter of the triangle is termed the area of the Triangle.
2. How to Find Area of Triangle?
Area of the Triangle can be calculated using the following formulas,
1. For a Right Triangle: Area = (1/2) ⨯ base ⨯ height
2. Using Heron’s Formula: Area = √(s ⨯ (s – a) ⨯ (s – b) ⨯ (s – c)), where “s” is the semi-perimeter.
3. What is Area of Triangle with 3 sides?
If all the three sides of triangle are given, then its area is calculated using the Heron’s Formula. Area = √{ s(s-a)(s-b)(s-c)}
where, a, b, and c are the sides of triangle and s is semi-perimeter = ½ (a+b+c)
4. How To Find Area Of Triangle Without Height?
Without height, the area of triangle can be calculated using the Heron’s formula, which is :
Area of a triangle = √{s(s-a)(s-b)(s-c)}
where, a, b, and c are sides of the given triangle
and s = ½ (a+b+c) is the semiperimeter.
5. What is Area Of Equilateral Triangle?
Area of equilateral triangle is given by the following formula :
A = (√3)/4 × side2.
6. What is Area Of Isosceles Triangle?
Area of Isosceles Triangle is given by the following formula :
A = ¼ × b√(4a2 – b2), where a= the two equal sides and b= the third side.
7. What is Area of Triangle in Coordinate Geometry?
When all three vertices of the triangle A(x1, y1), B(x2, y2) and C(x3, y3) are given then its area is calculated using the formula,Area = 1/2 × [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
8. What is Area of Triangle in Vector form?
If a triangle is formed by two vectors u, and v then its area is given by half of magnitude of product of the given vectors i.e.Area = 1/2| ×
× |
|
Share your thoughts in the comments
Please Login to comment...