Congruence of triangles is the property of two triangles in which all three corresponding sides and corresponding angles are equal. Two triangles are said to be congruent if and only if they can be overlapped with each other completely.
In this article, we are going to learn about the different criteria for the Congruence of Triangles with the help of solved examples.
What are Congruent Triangles?
Congruent triangles are triangles that are perfect copies of one another. Various congruence rules are used to prove the congruency in two triangles.
Congruent triangles if arranged in proper orientation are mirror images of each other. The corresponding angle and dimensions of congruent figures are the same.
The symbol used to show congruency between two objects is “≅”. To show congruency between them we write Δ ABC ≅ Δ PQR.

CPCT Full Form
The full form of CPCT is Corresponding Parts of Congruent Triangles. This is a fundamental rule used to establish equality of various parts of triangles based on their congruence.
It states that if two triangles are congruent, then each of their corresponding parts (angles and sides) are equal.
Congruence of Triangles Rules
The different criteria used to prove congruency between two triangles are:
- SSS Criteria: Side-Side-Side
- SAS Criteria: Side-Angle-Side
- ASA Criteria: Angle-Side-Angle
- AAS Criteria: Angle-Angle-Side
- RHS Criteria: Right angle- Hypotenuse-Side
They are also called the postulates or rules for the congruence of triangles. Let’s discuss them in detail.
SSS (Side, Side, Side) Congruence Rule
In the postulate of SSS, if all three sides of a triangle are equal to the corresponding three sides of another triangle, then it satisfies the condition of SSS.

In the above-given figure, we can see that,
AB = QR,
BC = RP, and
CA = PQ .
Hence, Δ ABC ≅ Δ QRP
Read More about SSS Congruence Rule.
SAS (Side, Angle, Side) Congruence Rule
In the postulate of SAS, in comparison among two triangles, if two sides and the angle included between two sides are equal. Then it satisfies the condition of SAS.

In the above-given figure, we can see that,
CB = RQ,
BA = QP, and
∠B = ∠Q.
Hence, Δ CBA ≅ Δ RQP.
Read More about SAS Congruence Rule.
ASA (Angle, Side, Angle) Congruence Rule
Here, if we are having two triangles, where any two angles and sides included between the two angles of one triangle are equal to the angles and sides of the corresponding triangle. Then the two triangles will satisfy the ASA congruency.

In the above-given figure, we can see that,
AB = PQ,
∠A = ∠P, and
∠B = ∠Q.
Hence, ΔACB ≅ ΔPQR.
Read More about ASA Congruence Rule.
AAS (Angle, Angle, Side) Congruence Rule
If any two angles of a triangle and non-included side are equal to the two angles and side of the corresponding triangle, then it will satisfy the AAS congruency.

From the given figure, we can say that,
BC = QR,
∠A = ∠P, and
∠B = ∠Q
Hence, ΔACB ≅ ΔDFE
RHS (Right Angle- Hypotenuse- Side) Congruence Rule
In RHS congruency, if only two sides i.e. hypotenuse and one side of a right-angled triangle are equal to the corresponding hypotenuse and side of another right-angled triangle, then we can say that RHS Congruence Rule is satisfied.

From the above-given example of a right-angled triangle, we get
∠B = ∠Q (right angles)
CA = RP and
AB = PQ.
Hence, ΔACB ≅ ΔDFE.
Note– RHS criteria of congruence get satisfied only with a right-angled triangle.
Read More about RHS Congruence Rule.
Properties of Congruent Triangles
Congruent triangles have the following key properties :
- Congruent Triangles are mirror images of each other.
- Congruent Triangles perfectly overlap each other if arranged in the proper orientation.
- Corresponding parts of Congruent Triangles are equal.
- Congruent Triangles have the same area.
Read More :
Difference between Similar Triangles and Congruent Triangles
| Similar Triangles |
Congruent Triangles |
|
Similar Triangles vs. Congruent Triangles
|
| Similar triangles. are triangles in which ratios of their sides are equal. |
Congruent Triangles are triangles that have equal corresponding parts. |
| Area of similar triangles may or may not be equal. |
Area of congruent triangles is equal. |
| Similar triangles can’t overlap each other. |
Congruent triangles overlap each other completely. |
|
Similarity in the triangles is proved by the condition
AAA Rule: Angle-Angle-Angle
|
Congruency in the triangles is proved by the condition
SSS Rule: Side-Side-Side
SAS Rule: Side-Angle-Side
ASA Rule: Angle-Side-Angle
AAS Rule: Angle-Angle-Side
RHS Rule: Right angle- Hypotenuse-Side
|
Related :
Solved Examples on Congruent Triangles
Let’s solve some questions on the congruence of triangles.
Example 1: Check whether the given triangles are congruent or not also, write the congruency criteria for congruency in triangles.

Solution:
To identify the congruency in the above triangle.
BC = QR = 4 units (given)
CA = RP = 5 units (given)
∠ABC = ∠PQR = 90°
Now, we can conclude that Δ ABC ≅ Δ PQR by the RHS congruency condition.
Example 2: Check whether the given triangles are congruent or not also, write the congruency criteria for congruency in triangles.

Solution:
To identify the congruency in the above triangle.
BC = QR = 6 units (given)
CA = RP = 5 units (given)
AB = PQ = 9 units (given)
Now, we can conclude that Δ ABC ≅ Δ PQR by the SSS congruency condition.
Example 3: Check whether the given triangles are congruent or not also, write the congruency criteria for congruency in triangles.

Solution:
To identify the congruency in the above triangle.
AC = QR = 5 units (given)
∠BAC = ∠PQR (given)
BA = PQ = 9 units (given)
Now, we can conclude that Δ BAC ≅ Δ PQR by the SAS congruency condition.
Example 4: Check whether the given triangles are congruent or not also, write the congruency criteria for congruency in triangles.
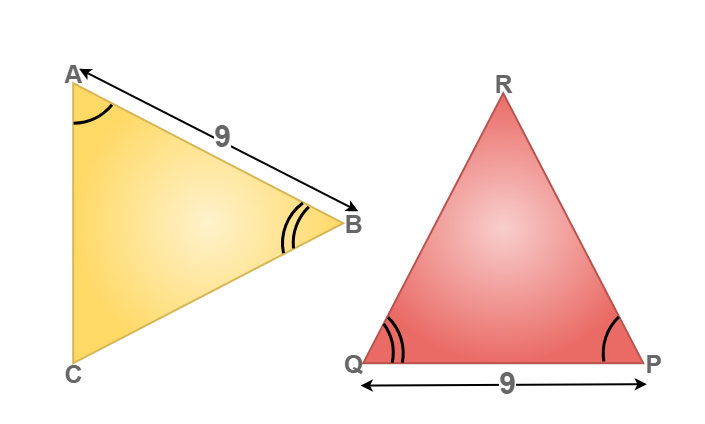
Solution:
To identify the congruency in the above triangle.
∠BAC = ∠PQR (given)
BA = PQ = 9 units (given)
∠CAB = ∠QPR (given)
Now, we can conclude that Δ BAC ≅ Δ PQR by the ASA congruency condition.
Example 5: Check whether the given triangles are congruent or not also, write the congruency criteria for congruency in triangles.
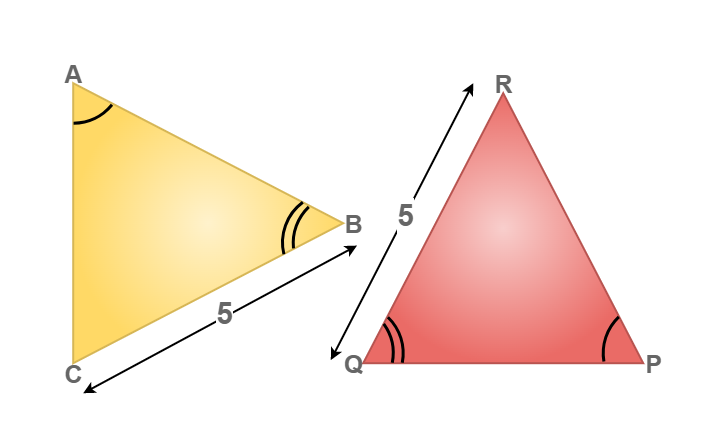
Solution:
To identify the congruency in the above triangle.
BC = QR = 5 units (given)
∠ABC = ∠PQR (given)
∠BAC = ∠QPR (given)
Now, we can conclude that Δ ABC ≅ Δ PQR by the AAS congruency condition.
Congruent Triangles- FAQs
What are Congruent Triangles?
Congruent triangles are triangles that can overlap one another if arranged in a specific orientation. All three corresponding sides and corresponding angles in a congruent triangle are equal.
What are the Rules of Congruency?
The five main rules for congruency of triangles are
SSS Rule: Side-Side-Side
SAS Rule: Side-Angle-Side
ASA Rule: Angle-Side-Angle
AAS Rule: Angle-Angle-Side
RHS Rule: Right angle- Hypotenuse-Side
What is the Full Form of CPCT.
CPCT is an abbreviation for Corresponding Parts of Congruent Triangles. CPCT says if two or more triangles are congruent to each other, then the corresponding angles and the corresponding sides of the triangles are also congruent to each other.
What is SSS Rule of Congruency in Triangles?
If all the three corresponding sides of two corresponding triangles are equal then the triangles are said to be congruent by SSS congruency condition.
What is SAS congruence of triangles?
The SAS (Side-Angle-Side) Congruence of triangles states hat if two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the triangles are congruent.
What is ASA congruency of triangles?
ASA (Angle-Side-Angle) congruence of triangles states that if two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the triangles are congruent.
What is AAS congruency?
AAS (Angle-Angle-Side) congruence states that if two angles and a non-included side of one triangle are equal to the corresponding two angles and side of another triangle, then the two triangles are congruent.
What is RHS congruency?
RHS (Right angle-Hypotenuse-Side) congruency states that if the hypotenuse and one other side of a right-angled triangle are equal to the corresponding hypotenuse and side of another right-angled triangle, then the two triangles are congruent.
Is the AAA criterion used for proving congruency in triangles?
No, AAA criterion cant be used for proving congruency in triangles. AAA criterion can be used for proving Similarities between two triangles.
All similar triangles are congruent. True or False?
No, all similar triangles are not congruent, but all congruent triangles are similar.
Share your thoughts in the comments
Please Login to comment...