Square is a type of quadrilateral with four sides. What distinguishes a square from other quadrilaterals is that all four sides of a square are of equal length, and all four interior angles are right angles (90 degrees).
Let’s learn about Square in detail, including its properties, area, perimeter and examples.
Square Definition
Square is a quadrilateral whose all four sides are equal and measure of each angle is 90°.
A square is made up of two pairs of parallel lines. All four sides of a square are equal. Its opposite sides are parallel to each other and the interior angles are equal to 90°.
Square Shape
A square is a type of four-sided shape known as a polygon. What makes a square unique is that all of its sides have the same length, and all of its angles measure exactly 90 degrees. When you cut a square perfectly in half using a plane that passes through its center, both resulting halves will be mirror images of each other.
Square Examples
A square is a very common shape and can be seen in a variety of objects which we use in our daily lives. Various Square-shaped objects are chess boards, carrom boards, Ludo, etc.

Properties of Square
Some general properties of the square are :
- Square is a quadrilateral with 4 sides and 4 vertices.
- All four sides of the square are equal.
- Opposite pairs of sides of a square are parallel to each other.
- Each interior angle of a square is 90°.
- Diagonals of a square are perpendicular bisectors of each other.
- Diagonals of a square are of equal length.
- Sum of all interior angles of a square is 360°.
- Diagonals of a square divide it into two congruent triangles.
We know that a square is a four-sided figure with equal sides. There are three basic square formulas that are commonly used in geometry for squares are,
Let us learn these square formulas in detail.
Area of Square
Area of a square is defined as the total space occupied inside its boundaries. The formula for calculating the area of a square with sides ‘a’ is given by the formula,
Area of Square = a2
Area of Square (When Diagonal is Given)
If the diagonal of a square is given then the area of the square is given by
Area = d2/2
Perimeter of Square
Perimeter of a square is defined as the length of all its boundaries. Suppose the length of the sides of a square is ‘a’ then its perimeter is given by
Perimeter of Square = Sum of All Sides of Square = a + a + a + a
Perimeter of Square = 4a units
As a result, 4a is perimeter of a square with each side’s length equal to ‘a’ units.
Diagonal of Square
Diagonals of square is equal to a√2, where a is the side of the square. The length of both diagonals of a square is equal to each other. The relation between diagonals and sides of a square is given by Pythagoras Theorem.
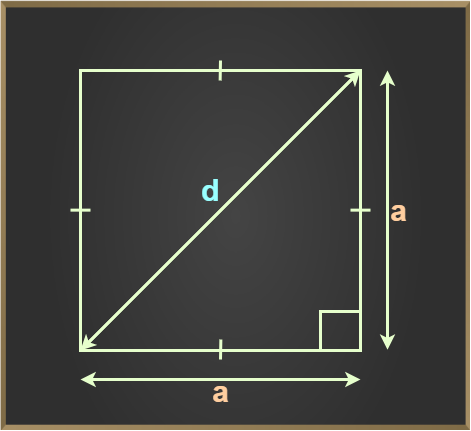
Length of Diagonal of Square
Length of diagonal of a square is calculated using Pythagoreas Theorem as,
Hypotenuse2 = Base2 + Perpendicular2
Hence,
Diagonal2 = Side2 + Side2
d2 = s2 + s2
d2 = 2s2
d = s√2
Construction of Square
Square in geometry can be constructed using the steps added below,
For example, Construct asquare with sides 4 cm.
Step 1: Draw a line segement AB of 4 cm
Step 2: From point A and B draw two right angles.
Step 3: Take an arc of 4 cm and mark on right angles from A and B and mark these points C and D respectively.
Step 4: Join CD, ABCD is the required square.
Related :
Examples on Squares
Some Examples on Square Formulas are,
Example 1: A square has one of its sides measuring 24 cm. Calculate its area and perimeter.
Solution:
Given,
Area of Square = a2
Area of Square = 24 × 24 = 576 sq cm
Perimeter of Square = Sum of all sides of square = a + a + a + a = 4a
P = 4 × 24
P = 96 cm
Hence, area of square is 576 sq. cm and perimeter of square is 96 cm.
Example 2: Find the area of a square park whose perimeter is 420 ft.
Solution:
Given,
- Perimeter of Square Park = 420 ft
Perimeter of a Square = 4 × side
4 × side = 420
Side = 420/4
Side = 105 ft
Formulae for Area of a Square = side2
Hence, Area of Square Park = (105)2
A = 105 × 105 = 11025 ft2
Thus, area of a square park whose perimeter is 420 ft is 11025 ft2
Example 3: A rectangular floor is 40 m long and 30 m wide. Square tiles, each of 4 m side lengths, are to be used to cover the floor. What will be the total number of tiles which will be required to cover the floor?
Solution:
Given,
- Length of Floor = 40 m
- Breadth of Floor = 30 m
Area of Rectangular Floor = length × breadth = 40 m × 30 m = 1200 sq. m
Side length of one tile = 4 m
Area of one tile = side × side = 4 m × 4 m = 16 sq. m
Now number of tiles needed = Total Area of Floor / Area of One Tile = 1200 /16 = 75 tiles
Total 75 tiles are needed to cover the area of rectangular floor of 1200 sq m.
Example 4: Find the area of a square park whose diagonal is 15 m.
Solution:
Given,
- Diagonal of Square Park = 15 m
Area of a Square Formula when Diagonal is Given = (d)2 / 2
Hence, Area of Square Park = (15)2/ 2
A = (15 × 15) / 2 = 225 / 2 = 112.5 sq. m
Thus, area of a square park whose diagonal is 15 m is 112.5 sq. m.
Practice Questions on Square
Various practice questions on square are,
Q1: Find the perimeter of a square of its side 24 in.
Q2: If the side of a square chess board is 120cm in, then find its perimeter.
Q3: What is area and perimeter of a square if its side is 15 cm?
Frequently Asked Questions on Square
What are Squares in Maths?
A square is a polygon, with all sides equal and opposite sides parallel to each other. Angles in a square are equal and the measure of each angle is 90 degrees.
What is Area and Perimeter of Square Formula?
- Area of a Square is, Area = (side)2
- Perimeter of a Square is, Perimeter = 4 x side.
Can Rhombus be considered a Square?
No, a rhombus is not a square, but every square can be considered a rhombus.
Is Square a Polygon?
Square is a closed figure formed by four straight lines So it is considered a quadrilateral. Every quadrilateral is a polygon. So a square is a polygon.
Is Square Different From Rectangle?
Yes, a square is different from Rectangle. In a square, all its sides are equal whereas in a rectangle only its opposite sides are equal.
How is a Square Different from a Rhombus?
Square and Rhombus both are Equilateral Quadrilaterals, i.e. both have equal all four sides. The difference between them is that all angles in a square are equal and right angles, but on the other hand all the angles of a rhombus need not be equal.
Hence, Rhombus with right angles is called a Square. Thus, “Every Square is a Rhombus but all Rhombus are not Squares.”
Share your thoughts in the comments
Please Login to comment...