Class 12 RD Sharma Solutions – Chapter 22 Differential Equations – Exercise 22.6
Last Updated :
19 Jan, 2021
Question 1. Solve the following differential equation
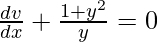
Solution:
From the question it is given that,
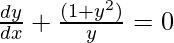
Transposing we get,
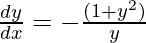
By cross multiplication,
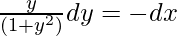
Integrating on both side, we will get,
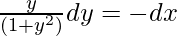
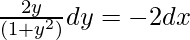
log (1 + y2) = – 2x + c1
Therefore,  log [1 + y2] + x = c
log [1 + y2] + x = c
Question 2. Solve the following differential equation
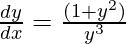
Solution:
From the question it is given that,
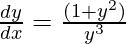
By cross multiplication,
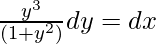
Integrating on both side, we will get,
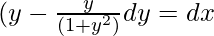
![Rendered by QuickLaTeX.com ∫ydy - ∫\frac{y}{(1 + y^2)} dy = ∫ dx\\ ∫ydy - \frac{1}{2} ∫\frac{2y}{(1 + y2)} dy = ∫ dx\\ \frac{y^2}{2} - \frac{1}{2} log [y^2 + 1] = x + c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b9b770593ebd84ec47c12cc5d3147d13_l3.png)
Question 3. Solve the following differential equation:
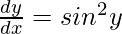
Solution:
From the question it is given that,
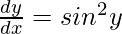
By cross multiplication,
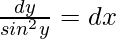
As we know that, 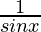 = cosec x
= cosec x
cosec2y dy = dx
Integrating on both side, we will get,
∫cosec2 y dy = ∫dx + c
– cot y = x + c
Question 4. Solve the following differential equation:
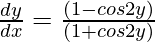
Solution:
From the question it is given that,
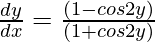
We know that, 1 – cos 2y = 2sin2y and 1 + cos 2y = 2 cos2y
So, 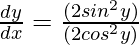
Also we know that, 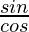 = tan θ
= tan θ
By cross multiplication,
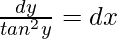
Integrating on both side, we get,
∫cot2y dy = ∫dx
∫ (cosec2y – 1) dy = ∫dx
– cot y- y + c = x
c = x + y + cot y
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...