A quadratic equation is a second-degree equation that can be represented as ax2 + bx + c = 0. In this equation, x is an unknown variable, a, b, and c are constants, and a is not equal to 0.
Details Quadratic Equations:
- Coefficients: a and b are the coefficients, and c is the constant term.
- Roots: Since variable x is of the second degree, there are two roots or answers for this quadratic equation.
- Leading coefficient: “a” is called the leading coefficient.
- Absolute term: “c” is called the absolute term of f (x).
- Discriminant: Part (b2 – 4ac) is called the “discriminant”. When it is positive, we get two real solutions. When it is zero we get just ONE solution.

Graphical Illustration of a Quadratic Equation
Let’s learn how to solve Quadratic Equations using different methods in detail.
What is Quadratic Equation?
Quadratic Equation is a polynomial equation of degree two. The solutions of a quadratic equation are known as its roots. These roots can be found using methods like factoring, completing the square, using the quadratic formula, or graphing.
Roots of a quadratic equation are:
[-b ± √(b²-4ac)]/(2a) if b2 – 4ac ≥ 0
Quadratic equation is defined as a polynomial equation of second degree, which means it contains a variable raised to the power of 2 (squared) as its highest exponent.
Quadratic Equation Standard Form
Standard Form of Quadratic Equation is:
ax2 + bx + c = 0
where,
- x is Variable of Equation
- a, b, and c are Real Numbers and Constants and a ≠ 0
In general, any second-degree polynomial P(x), in form of P(x) = 0 represents a Quadratic Equation.
Quadratic Equation Examples
Some examples of quadratic equations are:
- x2 – 11x + 28
- 3x2 – 11x + 23 = 0
- 5x2 = 0
- 11x2 -13 = 0
Roots of Quadratic Equation
Values of xo which satisfies the quadratic equation q(x) are called the roots of the quadratic equation. This implies that for any xo if q(x) = 0. Then xo is the root of the q(x).
For example, the roots of the quadratic equation q(x): 3x2 – 10x – 8 = 0 are x = -2/3 and x = 4.
For x = -2/3,
q(-2/3) = 3(-2/3)2 – 10(-2/3) – 8
⇒ q(-2/3) = 4/3 + 20/3 – 8
⇒ q(-2/3) = 0
For x = 4,
q(4) = 3(4)2 – 10(4) – 8
⇒ q(4) = 32 – 40 -8
⇒ q(4) = 0
Note: Quadratic equation is a two degrees polynomial i.e., it can have a maximum of 2 roots.
Easiest and most efficient way to calculate the roots of the quadratic equation is using the quadratic formula. Quadratic formula to solve the general quadratic equation ax2 + bx + c = 0 is given in the following image:

Quadratic Formula
Nature of Roots
We can easily find the nature of the roots of the quadratic equations without actually finding the roots. Generally, we represent the roots of quadratic equations with α and β symbols.
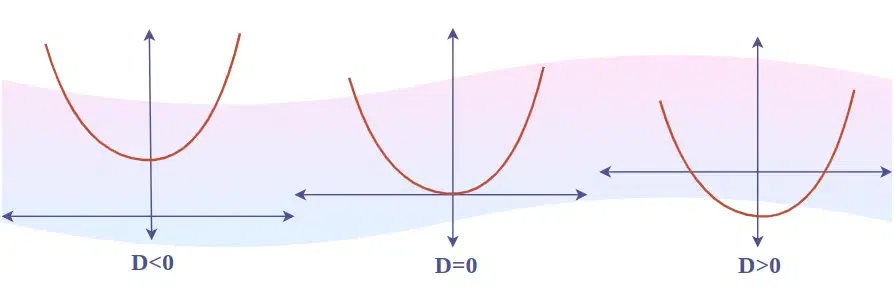
Discriminant
Discriminant provides important information about the nature and type of the roots of the equation. It is usually denoted as D or Δ.
Formula of discriminant of a quadratic equation is given by:
D = b2 – 4ac
Let’s understand the discriminant of a quadratic equation and the corresponding nature of its roots.
|
Discriminant and Nature of Roots
|
| Discriminant (D) |
Nature of Roots |
Description |
| D > 0 |
Real and Distinct |
The quadratic equation has two real and distinct roots. |
| D = 0 |
Real and Equal |
The quadratic equation has two real and equal (coincident) roots. |
| D < 0 |
Complex or Imaginary |
The quadratic equation has no real roots; instead, it has two complex or imaginary roots. |
Quadratic Equation Sum of Roots
For a given quadratic equation ax2 + bx + c = 0, the sum of roots can be found with the help of the coefficient of x2, and coefficient of x.
For example, let’s suppose we have a quadratic equation, equal to ax2 + bx + c = 0
Formula for Sum of roots of Quadratic Equation :
Sum of Roots: α + β = -b/a = -Coefficient of x/ Coefficient of x2
Quadratic Equation Product of Roots
For a quadratic equation of the form, ax2 + bx + c = 0, the product of roots can be found with the help of the coefficient of x2, and the constant term.
Formula for Product of Roots of Quadratic Equation :
Product of Roots: αβ = c/a = Constant term/ Coefficient of x2
Let’s try to understand the formulas for the sum and product of roots of a quadratic equation with the help of an example.
Example: Find the sum and the product of the roots of equation 2x2 + 5x + 3 = 0.
Solution:
Given quadratic equation, 2x2 + 5x + 3 = 0
Comparing with, ax2 + bx + c = 0
We get, a = 2, b = 5, c =3
- Sum of Roots = α + β = -b/a = -5/2
- Product of Roots = αβ = c/a = 3/2
Writing Quadratic Equations using Roots
If the roots of the quadratic equation α, and β are given then we can easily write the quadratic equation by using the formula,
(x – α)(x – β) = 0
- If the sum (α + β) and the product (αβ) of the quadratic equation then the quadratic equation is given using x2 – (α + β)x + αβ = 0.
Let’s understand this with the help of an example.
Example: Find the quadratic equation whose roots are, 1 and 2.
Solution:
Given, α = 1 and β = 2
Then the required quadratic equation is,
(x – α)(x – β) = 0
⇒ (x – 1)(x – 2) = 0
⇒ x2 – 2x -x + 2 = 0
⇒ x2 – 3x + 2 = 0
This is the required quadratic equation.
We can also find the quadratic equation if the sum and the product of the quadratic equation are given. Let us suppose the sum (S) and the product (P) of the quadratic equation are (α + β) and αβ respectively.
Formula to write Quadratic Equation when Sum and Product of Roots are given :
x2 – (Sum)x + (Product) = 0
or, x2 – (α + β)x + αβ = 0
Example: Find the quadratic equation whose sum of the roots is, 3 and the product of the root are 2.
Solution:
Given, α + β = 3 and αβ = 2
Then the required quadratic equation is,
x2 – (α + β)x + αβ = 0
⇒ x2 – 3x + 2 = 0
This is the required quadratic equation.
How to Solve Quadratic Equations?
Let’s assume a quadratic equation P(x) = 0. The points which satisfy this equation are called solutions or roots of this quadratic equation.
These are the four common methods to find the solutions of a quadratic equation:
- Factorization Method
- Completing the Square Method
- Using the Quadratic Formula
- Graphical Method
Let’s look at all these methods one by one through examples.
Factorization Method
Solving quadratic equations by factoring is a fundamental method in algebraic problem-solving. The process involves rewriting the quadratic equation in the form ax + bx + c = 0 and then factoring the quadratic expression into two binomial factors.
One effective technique often employed in this process is “splitting the middle term“.
This method involves finding two numbers that multiply to the product of the leading coefficient (a) and the constant term (c) and add up to the coefficient of the linear term (b).
By splitting the middle term into these two numbers and then factoring by grouping, the quadratic expression can be factored into two binomial factors. Once factored, the equation is solved by setting each binomial factor equal to zero and solving for the variable (x). This method provides a systematic approach to solving quadratic equations efficiently and accurately, making it a valuable tool in algebraic problem-solving strategies.
A quadratic equation can be considered a factor of two terms. Like ax2 + bx + c = 0 can be written as (x – x1)(x – x2) = 0 where x1 and x2 are roots of quadratic equation.
Steps of Solving Quadratic Equations Using Factorization method:
Step 1: Find two numbers such that the product of the numbers is ‘ac’ and the sum is ‘b’.
Step 2: Then write x coefficient as the sum of these two numbers and split them such that you get two terms for x.
Step 3: Factor the first two as a group and the last two terms as another group.
Step 4: Take common factors from these and on equating the two expressions with zero after taking common factors and rearranging the equation we get the roots.
Let’s consider an example of this for better understanding.
Example: Find out the solutions of the given quadratic equation using the factorization method.
2x2 – 3x + 1 = 0
Solution:
Given, 2x2 – 3x + 1 = 0
⇒ 2x2 – 2x – x + 1 = 0
⇒ 2x(x – 1) – 1(x -1) = 0
⇒ (2x – 1)(x-1) = 0
Now this equation is zero when either of these two terms or both of these terms are zero
So,
Putting 2x – 1 = 0, we get x = 1/2
Similarly, x – 1 = 0, we get x = 1
Thus, we get two roots x = 1 and 1/2
Completing Square Method
Any equation ax2 + bx + c = 0 can be converted in the form (x + m)2 – n2 = 0. After this, we take the square roots and get the roots of the equation.
Completing the square is just a way to readjust the given quadratic equation in such a way that they come in the form of squares. Let’s see this through an example.
Example: Find the root of the given equation through complete the square method.
x2 + 4x – 5 = 0
Solution:
Given, x2 + 4x – 5 = 0
Solving by Completing Square Method
x2 + 4x – 5 = 0
⇒ x2 + 4x + 4 – 9 = 0
⇒ (x + 2)2 – 32 = 0
⇒ (x + 2)2 = 32
Taking square root both sides,
x + 2 = 3 and x + 2 = -3
⇒ x = 3 -2 and x = -3 -2
⇒ x = 1 and x = -5
We have already discussed how to solve quadratic equations using the Quadratic Formula.
Quadratic Equation Graph Method
Let us suppose the general form of the quadratic equation is ax2 + bx + c = 0, where a ≠ 0. The quadratic equation is a polynomial equation of degree 2, so it comes under the conic section.
Further simplifying the standard form of quadratic equation,
y = ax2 + bx + c
⇒ y = a[(x + b/2a)2 – (D/4a2)]
⇒ y – D/4a = a[(x + b/2a)2]
This resembles a parabola and we can easily draw its curve. The points where this curve cut the x-axis are the roots of the quadratic equation (or zeroes of the quadratic polynomial).

Quadratic Equation Graphical Method
Quadratic Equations Having Common Roots
Let’s take two quadratic equations, a1x2 + b1x + c1 = 0, and a2x2 + b2x + c2 = 0.
Then these equation will have common roots if (a1b2 – a2b1) (b1c2 – b2c1) = (a2c1 – a1c2)2
Let’s understand this with the help of an example.
Example: Check whether the equation 3x2 + 7x – 6 = 0 and the equation 6x2 + 14x – 12 = 0 have common roots or not.
Solution:
Given equations, 3x2 + 7x – 6 = 0 and 6x2 + 14x – 12 = 0
Comparing with a1x2 + b1x + c1 = 0 and a2x2 + b2x + c2 = 0 we get,
a1 = 3, b1 = 7 and c1 = -6
a2 = 6, b2 = 14 and c2 = -12
Using the above condition we get,
(a1b2 – a2b1) (b1c2 – b2c1) = (a2c1 – a1c2)2
⇒ (42 – 42)(-84 + 84) = (-36+36)2
⇒ 0 = 0
Thus, the above equations have common roots.
Maximum and Minimum Value of Quadratic Equation
We know that we can easily plot a graph of the quadratic equation in the form of q(x) = ax2 + bx + c and it comes out to be a parabola.

Maximum and Minimum Values of Quadratic Equation
Now, performing the necessary calculation we can state that:
- If a > 0, q(x) is minimum at x = -b/2a
- If a < 0, q(x) is maximum at x = -b/2a
Thus we can easily get the range of the quadratic equation.
- When a > 0, Range of q(x) is [q(-b/2a), ∞)
- When a < 0, Range of q(x) is (-∞, q(-b/2a)]
Maximum and Minimum values of the function is found by studying the cases added below:
Case 1: If a > 0 in ax2 + bx + c = 0,
- Then range of quadratic equation is [-D/4a, ∞)
Case 2: If a > 0 in ax2 + bx + c = 0,
- Then range of quadratic equation is (-∞, -D/4a)
We can also find the maximum and minimum value of the function in the given interval by using concept of Maxima and Minima.
Quadratic Equation Sign Convention
For a quadratic equation -ax2 + bx + c = 0,
- Roots of Quadratic Equation are equal in magnitude but have opposite sign if b = 0 and ac < 0
- When a > 0, c < 0 or a > 0, c > 0; the roots of quadratic equation have opposite sign
- Roots with greater magnitude is negative if sign of a = sign of b × sign of c.
Positive Coefficient (a > 0):
- If b and c are both positive, the polynomial will have no positive roots.
- If b and c are both negative, the polynomial will have two positive roots.
- If b and c have opposite signs, the polynomial will have one positive root.
Negative Coefficient (a < 0):
- If b and c are both positive, the polynomial will have two negative roots.
- If b and c are both negative, the polynomial will have no negative roots.
- If b and c have opposite signs, the polynomial will have one negative root.
Solved Examples on Quadratic Equation
Let’s solve some questions on quadratic equations using its formula.
Example 1: Check whether the following equation is a quadratic equation or not. (x – 2)(x + 1) = (x – 1)(x + 3)
Solution:
We know that a quadratic equation must be of degree 2.
Let’s simplify and check the given equation.
(x – 2)(x + 1) = (x – 1)(x + 3)
⇒ x2 + x – 2x – 2 = x2 + 3x – x – 3
⇒ x2 – x – 2 = x2 + 2x – 3
⇒ -x – 2 = 2x – 3
⇒ -3x + 1 = 0
This equation is of degree 1. Thus, it cannot be a quadratic equation.
Example 2: Find the quadratic equation having the roots 4 and 9 respectively.
Solution:
The quadratic equation having the roots α, β, is (x – α)(x – β) = 0
Given,
α = 4, and β = 9
Therefore the required quadratic equation is,
(x – 4)(x – 9) = 0
x2 – 9x – 4x + 36 = 0
x2 – 13x + 36 = 0
Thus, the required quadratic equation is x2 – 13x + 36 = 0
Example 3: Quadratic equation 3x2 + 5x + 9 = 0 has roots α, and β. Find the quadratic equation having the roots 1/α, and 1/β.
Solution:
Given equation 3x2 + 5x + 9 = 0
Comparing with ax2 + bx + c = 0
a = 3, b = 5 and c = 9
α + β = -b/a = -5/3
αβ = c/a = 9/3 = 3
Roots of the new equation are 1/α and 1/β.
Sum of Roots = 1/α + 1/β = (α + β)/α β = (-5/3)×(1/3) = -5/9
Product of Roots = 1/α β = 1/3
Thus, the required quadratic equation is,
x2 – (Sum)x + Product = 0
x2 – (-5/9)x + 1/3 = 0
Simplifying,
9x2 + 5x + 3 = 0
Quadratic Equation Worksheet
Here’s a worksheet on quadratic equations for you to solve:
1. Check if √3 and -√3 are are the roots of the Quadratic Equation x2 + √3x – 6 = 0.
2. Find the Roots of the Quadratic Equation 6x2 – 31x + 40 = 0 by Factorization Method.
3. Find the Roots of the Quadratic Equation x2 + 12x = -35 by Completing the Square Method.
4. Find the Roots of the Quadratic Equation 4 – 11x = 3x2.
Quadratic Equations Questions
Below are some practice questions on quadratic equations class 10 for CBSE students:
- Solve the equation x2−5x+6=0 using factoring.
- Find the roots of the equation 2x2+3x−2=0 using the quadratic formula.
- If one root of the equation 3x2−7x+2=0 is 2, find the other root.
- Determine the nature of the roots of the equation 4x2−12x+9=0 and verify your answer.
- Solve the equation 2x2−9x+5=0 by completing the square method.
- If the sum of the roots of the equation x2−8x+15=0 is 8, find the product of the roots.
- Determine the roots of the equation 3x2+5x+2=0 by factorization.
- If the roots of the equation x2−6x+k=0 are equal, find the value of k.
- Solve the equation 4x2−7x−2=0 by the method of trial and error.
- Find the roots of the equation x2+2x−8=0 by the graphical method.
Practice Questions on Quadratic Equation
1. What is the standard form of a quadratic equation?
- ax2 + bx + c = 0
- y = mx + b
- a2 + b2 = c2
- x + y = 1
2. In the quadratic equation ax2 + bx + c = 0, what does ‘a’ represent?
- Linear coefficient
- Constant term
- Quadratic coefficient
- Discriminant
3. What is the discriminant of a quadratic equation ax2 + bx + c = 0?
- b2 – 4ac
- 2ab – c
- a2 + b2
- 2b – a
4. When discriminant is greater than zero in a quadratic equation, what can be said about the solutions?
- No real solutions
- One real solution
- Two distinct real solutions
- Infinite solutions
5. Which method can be used to solve a quadratic equation when the discriminant is zero?
- Factoring
- Completing the square
- Quadratic formula
- Graphing
6. If a quadratic equation has complex roots, what can be said about the discriminant?
- It is greater than zero
- It is less than zero
- It is equal to zero
- It can be any value
7. What is the vertex form of a quadratic equation?
- y = ax2 + bx + c
- y = a(x – h)2 + k
- y = mx + b
- x = -b ± √(b2 – 4ac) / 2a
8. In the quadratic formula, what does the term ± represent?
- Plus or minus
- Multiply
- Divide
- Square root
9. If the quadratic equation is written in the form y = a(x – h)2 + k, what do the values h and k represent?
- x-intercepts
- y-intercepts
- Vertex coordinates
- Quadratic coefficient
10. What is the relationship between the roots of a quadratic equation and the coefficients in the equation?
- There is no relationship
- Roots are the opposite of the coefficients
- Roots are the reciprocals of the coefficients
- Roots are related to the discriminant
FAQs about Quadratic Equations
What are quadratic equations?
A polynomial equation of the second degree in one variable is called the quadratic equation. The general form of the quadratic equation is ax2 + bx + c = 0. Here, a and b are the coefficients of x2 and x terms respectively, and c is the constant term.
What is standard form of quadratic equation?
Standard Form of Quadratic Equation is ax2 + bx + c = 0
Give some examples of quadratic equations.
Some examples of quadratic equations are :
- 2x2 -x + 2
- 4x2 – 13x + 33= 0
- 8x2 = 0
- 13x2 -17 = 0
What is quadratic formula?
General formula to solve a quadratic equation of the form ax2 + bx + c = 0 is
x = [-b ± √(b2 – 4ac)]/2a
What is discriminant of quadratic equation?
For any quadratic equation of the form ax2 + bx + c = 0, we calculate the value b2 – 4ac this is called the discriminant of the quadratic equation. It is denoted by D. It is used to tell the nature of the roots of the quadratic equation.
What are the roots of quadratic equation?
The roots of a quadratic equation are the values of x that satisfy the equation ax2 + bx + c = 0 where, a, b, and c are Real Numbers and Constants and a ≠ 0.
How to factor a quadratic equation?
To factor a quadratic equation of the form, ax2 + bx +c =0:
- Find two numbers that multiply to ac (the product of the coefficient of x2 and the constant term) and add to b (the coefficient of x).
- Rewrite the middle term (bx) as the sum of two terms using the numbers found in step 1.
- Factor by grouping.
How is quadratic equation different from linear equation?
Quadratic Equation differs from Linear Equation in the manner that Quadratic Equation has degree two and can have maximum of two solutions while Linear Equation has degree one and can have only one solution at maximum.
How to solve quadratic equations graphically?
While solving Quadratic Equation ax2 + bx + c = 0 graphically we need to find where the curve of the quadratic equation cuts the x-axis. The coordinates at which the curve of the quadratic equation cuts the x-axis are the roots of the quadratic equations.
How to solve quadratic equations?
Quadratic equations can be solved using various methods, including factoring, completing the square, using the quadratic formula, or by graphing.
How to solve quadratic equations by factoring?
To solve quadratic equations by factoring, first set the equation to ax2+bx+c=0. Then, factor the quadratic expression into two binomial factors. Finally, solve for the variable x by setting each factor equal to zero and solving for x.
Share your thoughts in the comments
Please Login to comment...