Solving Quadratic Equations
Last Updated :
28 Mar, 2021
Quadratic Equations occur almost everywhere in our real life. For example, even the problem of designing a playground can be formulated as a quadratic equation. When so many situations give rise to quadratic equations, it sparks a genuine interest in looking for their solutions. Let’s say Q(x) = 0 is a quadratic equation. The solutions to a quadratic equation represent the points where this equation is satisfied that is Q(x) = 0. The solutions are also called roots/zeros of the quadratic equation. Let’s look at some approaches for solving the quadratic equations.
Quadratic Equation
A quadratic equation is a second-degree polynomial. Its general form is given by,
ax2 + bx + c = 0
a, b and c are real numbers while a ≠ 0. Its shape is a parabola that opens upwards or downwards depending upon the value of “a”.
Its solution is the point where the equation is satisfied. There are several methods of finding out a solution to the quadratic equation given as follows:
- Factoring
- Completing the square
- Quadratic Formula
Factoring
We try to factor out the equation such that we get the equation in form of the product of two terms. Then on equating these two terms to zero, we get the roots.
The following steps must be used for finding the roots with factorization:
- All the terms must be on one side of the equation, either LHS or RHS leaving zero on the other side.
- Factorize the equation
- Set the factors equal to zero to find the roots one by one.
Let’s look at this method in more detail using the examples below:
Question 1: Factorize the following equation and find its roots: 2x2 – x – 1 = 0
Solution:
2x2 – x – 1 = 0
⇒ 2x2 -2x + x – 1 = 0
⇒ 2x(x – 1) + 1(x – 1) = 0
⇒ (2x + 1) (x – 1) = 0
For this equation two be zero, either one of these or both of these terms should be zero.
So, we can find out roots by equating these terms with zero.
2x + 1 = 0
x = 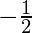
x – 1 = 0
⇒ x = 1
So, we get two roots in the equation.
x = 1 and 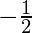
Question 2: Factorize the following equation and find its roots: x2 + x – 12 = 0
Solution:
x2 + x – 12 = 0
⇒ x2 + 4x – 3x – 12 = 0
⇒ x(x + 4) -3(x + 4) = 0
⇒ (x – 3) (x + 4) = 0
Equating both of these terms with zero.
x – 3 = 0 and x – 4 = 0
x = 3 and 4
Completing the Square
We try to bring the equation in the form of whole squares, for example: (x – a)2 – b2 = 0.
Steps for finding out roots by completing the square method:
Step 1: Bring the equation in the form ax2 + bx = -c.
Step 2: We need to make sure that a = 1 (if a≠1, multiply through the equation by 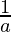 before going to next step.)
before going to next step.)
Step 3: Use the value of b from this new equation and 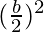 to both sides of the equation to form a perfect square on the left side of the equation.
to both sides of the equation to form a perfect square on the left side of the equation.
Step 4: Find the square root of the both sides of the equation.
Step 5: Solve the result to get the roots.
Let’s look at some examples regarding this,
Question 1: Find the roots of the following equation by completing the square’s method.
4x2 + 12x + 9 = 0.
Solution:
4x2 + 12x + 9 = 0
⇒ (2x)2 + 2(3)(2)x + 32 = 0
We can see that this equation is a perfect square,
⇒ (2x + 3)2 = 0
To find out the zeros in this equation,
2x + 3 = 0
x = 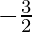
This equation has repeating root, which is x = 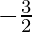
The above question had an equation that was a perfect square, but it might not be the case every time. In those cases, we will bring the equation in the above-given form using the steps that are mentioned.
Question 2: Find the roots of the equation by completing the square’s method.
9x2 + 24x + 3 = 0
Solution:
9x2 + 24x + 3 = 0
This equation can be re-written as,
⇒ 9x2 + 24x + 16 – 13 = 0
⇒ (3x)2 + 24x + 42 -13 =0
⇒ (3x + 4)2 -13 = 0
⇒ (3x + 4)2 -(√13)2 = 0
⇒ (3x + 4)2 = (√13)2
Taking square root of the both sides of the equation.
3x + 4 = √13 or 3x + 4 = -√13
We get our roots by solving these two equations,
3x + 4 = √13
x = 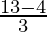
Similarly,
3x + 4 = – √13
x = 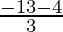
Quadratic Formula
All the quadratic equations can be solved using the quadratic formula.
For an equation of the form,
ax2 + bx + c = 0,
Where a, b and c are real numbers and a ≠ 0.
The roots of this equation are given by,
x = 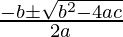
Given that b2 – 4ac is greater than or equal to zero.
Question 1: Find out the roots of the equation using Quadratic Formula,
4x2 + 10x + 3 = 0
Answer:
4x2 + 10x + 3 = 0
Using Quadratic Formula to solve this,
a = 4, b = 10 and c = 3
Before plugging in the values, we need to check for the discriminator
b2 – 4ac
⇒ 102 – 4(4)(3)
⇒ 100 – 48
⇒ 52
This is greater than zero, So now we can apply the quadratic formula.
Plugging the values into quadratic equation,
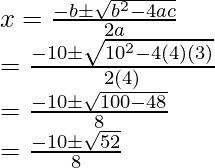
Question 2: Find out the roots of the equation using Quadratic formula,
5x2 + 9x + 4 = 0
Solution:
5x2 + 9x + 4 = 0
Using Quadratic Formula,
a = 5, b = 9 and c = 4.
Before plugging in the values, we need to check for the discriminator
b2 – 4ac
⇒ 92 – 4(5)(4)
⇒ 81 – 80
⇒ 1
This is greater than zero, So the quadratic formula can be applied. Plugging in the values in the formula,
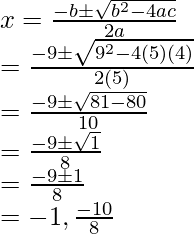
Share your thoughts in the comments
Please Login to comment...