Application of Derivative – Maxima and Minima | Mathematics
Last Updated :
18 Aug, 2020
The Concept of derivative can be used to find the maximum and minimum value of the given function. We know that information about and gradient or slope can be derived from the derivative of a function. We try to find a point which has zero gradients then locate maximum and minimum value near it. It is of use because it can be used to maximize profit for a given curve or minimizing loses or costs depending on the area of its usage.
Note: If
f(x) is a continuous function, then for every continuous function on a closed interval has a maximum and a minimum value.
Let f be a real-valued function and let a be an interior point in the domain of f. Then
- ‘a’ is called a point of local maxima if there is an h > 0 such that f(a) ≥f(x), for all x in (a – h, a + h), x≠a The value f(a) is called the local maximum value of f.
- ‘a’ is called a point of local minima if there is an h > 0 such that f(a) ≥ f(x), for all x in (a – h, a + h) The value f(a) is called the local minimum value of f
Note: Let
f be a function defined on an open interval
I. Suppose c ∈ I be any point. If
f has a local maxima or a local minima at x = c, then either f
‘(c) = 0 or f is not differentiable at c.
Steps to find maxima and minima –
First derivative test
- If
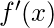 changes it’s sign from positive to negative then the point c at which it happens is local maxima.
changes it’s sign from positive to negative then the point c at which it happens is local maxima.
- If
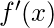 changes it’s sign from negative to positive then the point c at which it happens is local minima.
changes it’s sign from negative to positive then the point c at which it happens is local minima.
- If
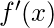 does not change it’s sign as x increases through c then the point is point of inflection.
does not change it’s sign as x increases through c then the point is point of inflection.
 In the above diagram C3 is global maxima and C4 local minima.
In the above diagram C3 is global maxima and C4 local minima.
Second derivative test
- Find values of x for which
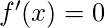 , these points are called critical points.
, these points are called critical points.
- Find
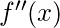 and put the values of x which was found above, if
and put the values of x which was found above, if -
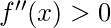 then the point is minima
then the point is minima
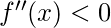 then the point is maxima
then the point is maxima 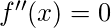 then we can not say anything, now we have to use first derivative to check whether the point is point of inflection, local minima or local maxima.
then we can not say anything, now we have to use first derivative to check whether the point is point of inflection, local minima or local maxima.
Stationary Point:
A point on which the tangent to the graph is horizontal is known as a stationary point, i.e the point at which
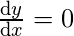
.
Note: If you have to find the maximum and minimum value of a function in a closed interval then find all the critical points by equating
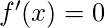
, then find the value of f(x) on all the points in the given interval [a, b].
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...