Puzzle: A car has 4 tyres and 1 spare tyre. Each tyre can travel a maximum distance of 20000 miles before wearing off. What is the maximum distance the car can travel before you are forced to buy a new tyre? You are allowed to change tyres (using the spare tyre) an unlimited number of times.
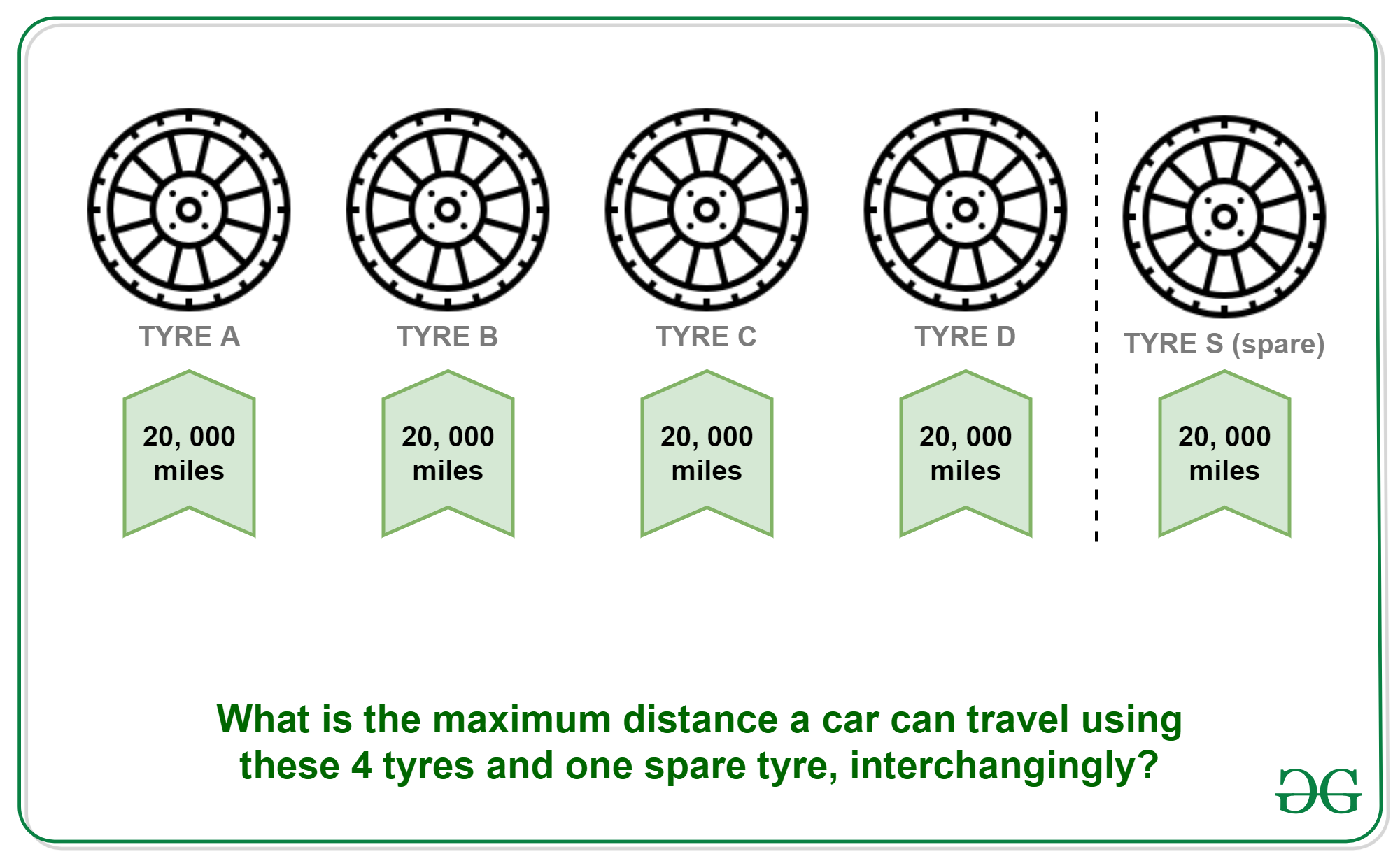
Answer: 25000 kms
Solution: Divide the lifetime of the spare tire into 4 equal part i.e., 5000 and swap it at each completion of 5000 miles distance.
Let four tyres be named as A, B, C and D and spare tyre be S.
- 5000 KMs: Replace A with S. Remaining distances (A, B, C, D, S) : 15000, 15000, 15000, 15000, 20000.
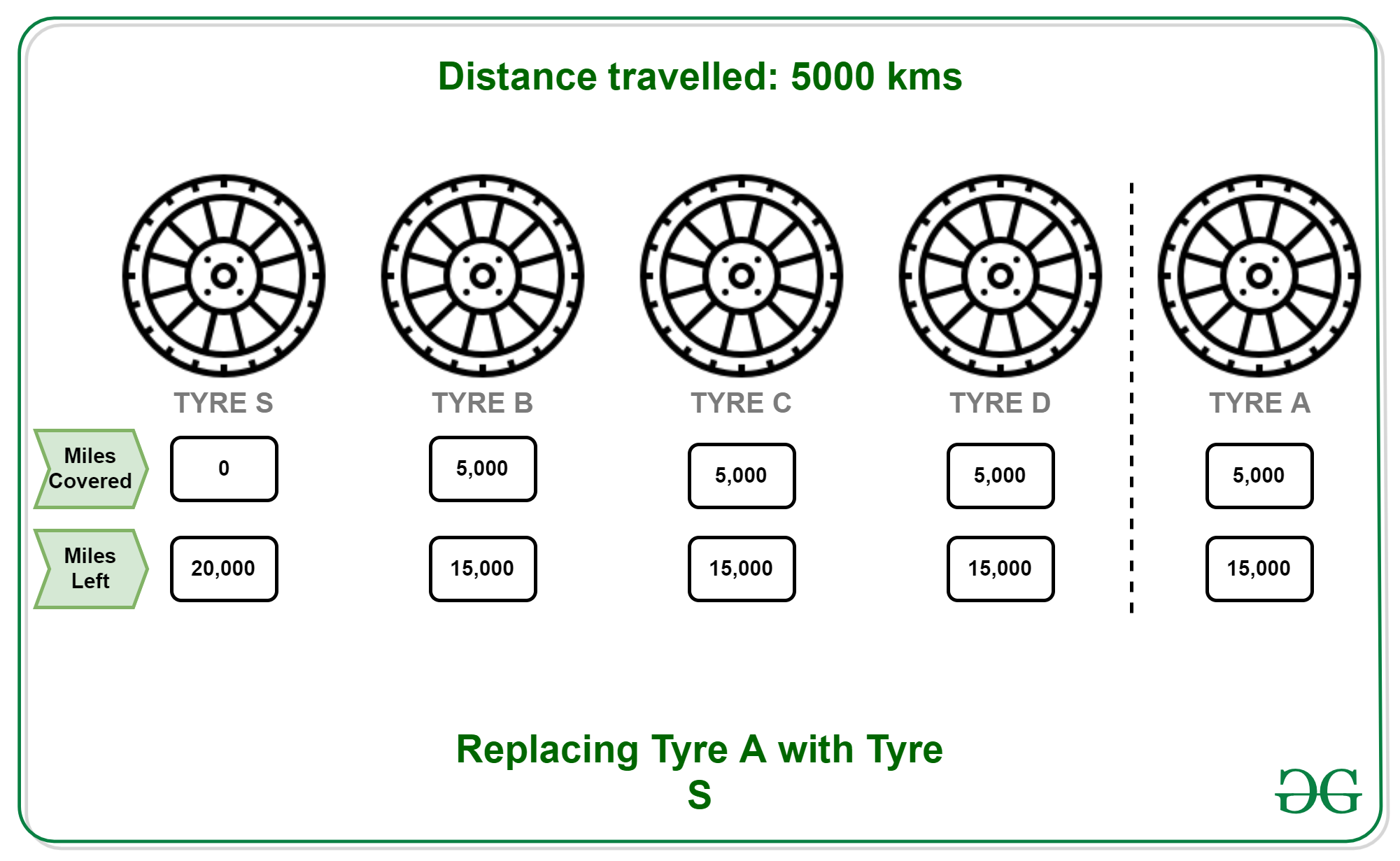
- 10000 KMs: Put A back to its original position and replace B with S. Remaining distances (A, B, C, D, S) : 15000, 10000, 10000, 10000, 15000.
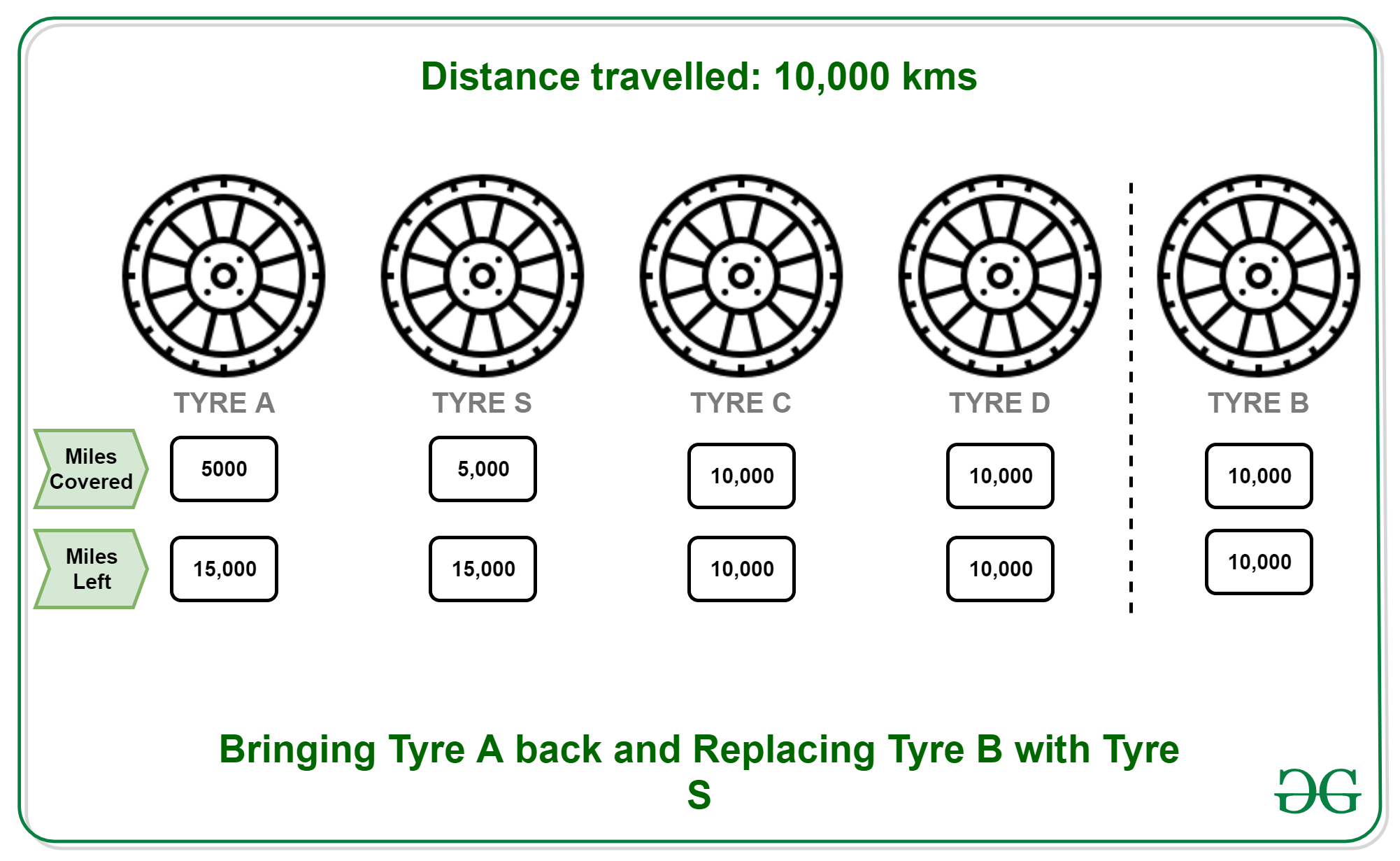
- 15000 KMs: Put B back to its original position and replace C with S. Remaining distances (A, B, C, D, S) : 10000, 10000, 5000, 5000, 10000.
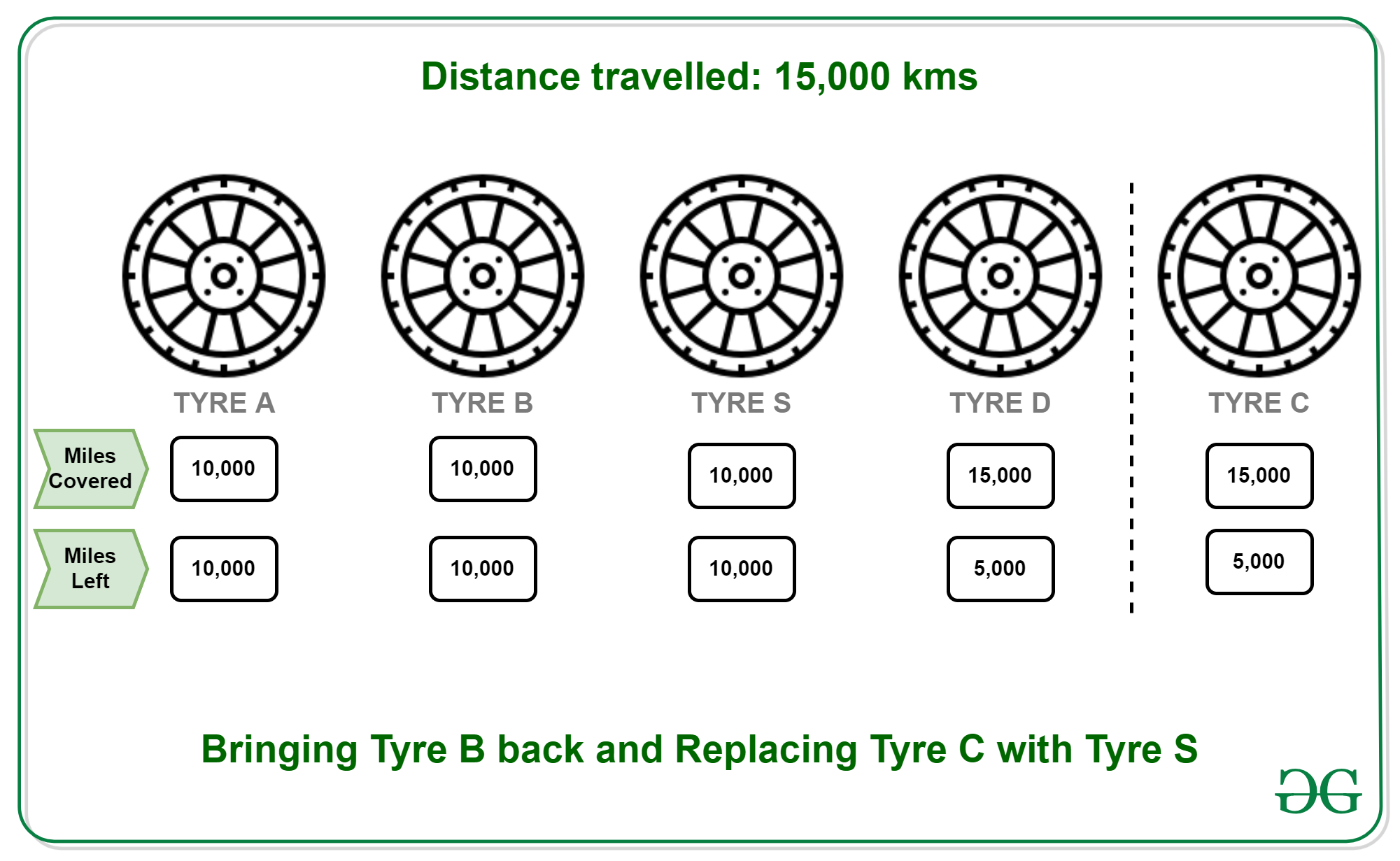
- 20000 KMs: Put C back to its original position and replace D with S. Remaining distances (A, B, C, D, S) : 5000, 5000, 5000, 0, 5000.
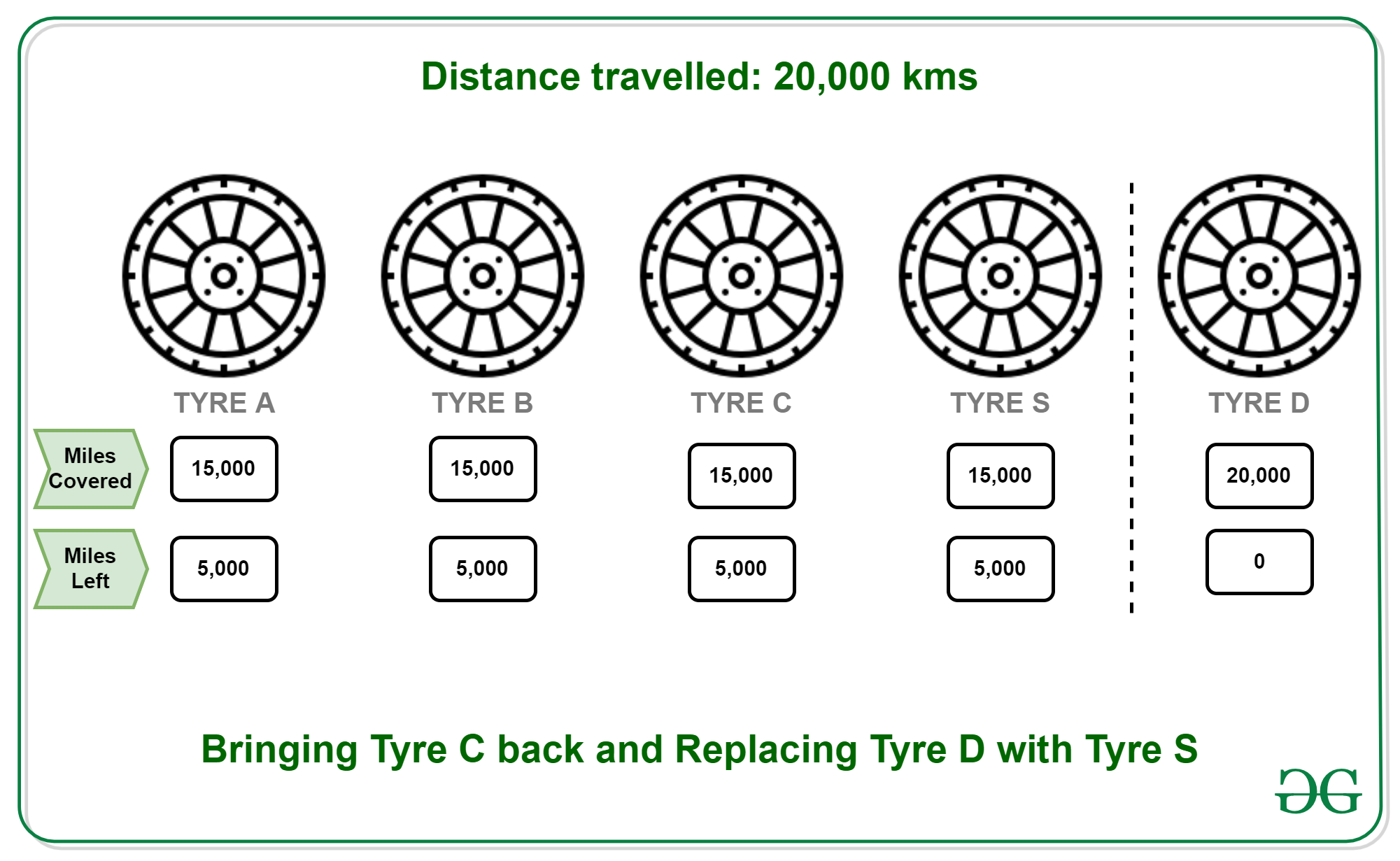
- 25000 KMs: Every tyre is now worn out completely.
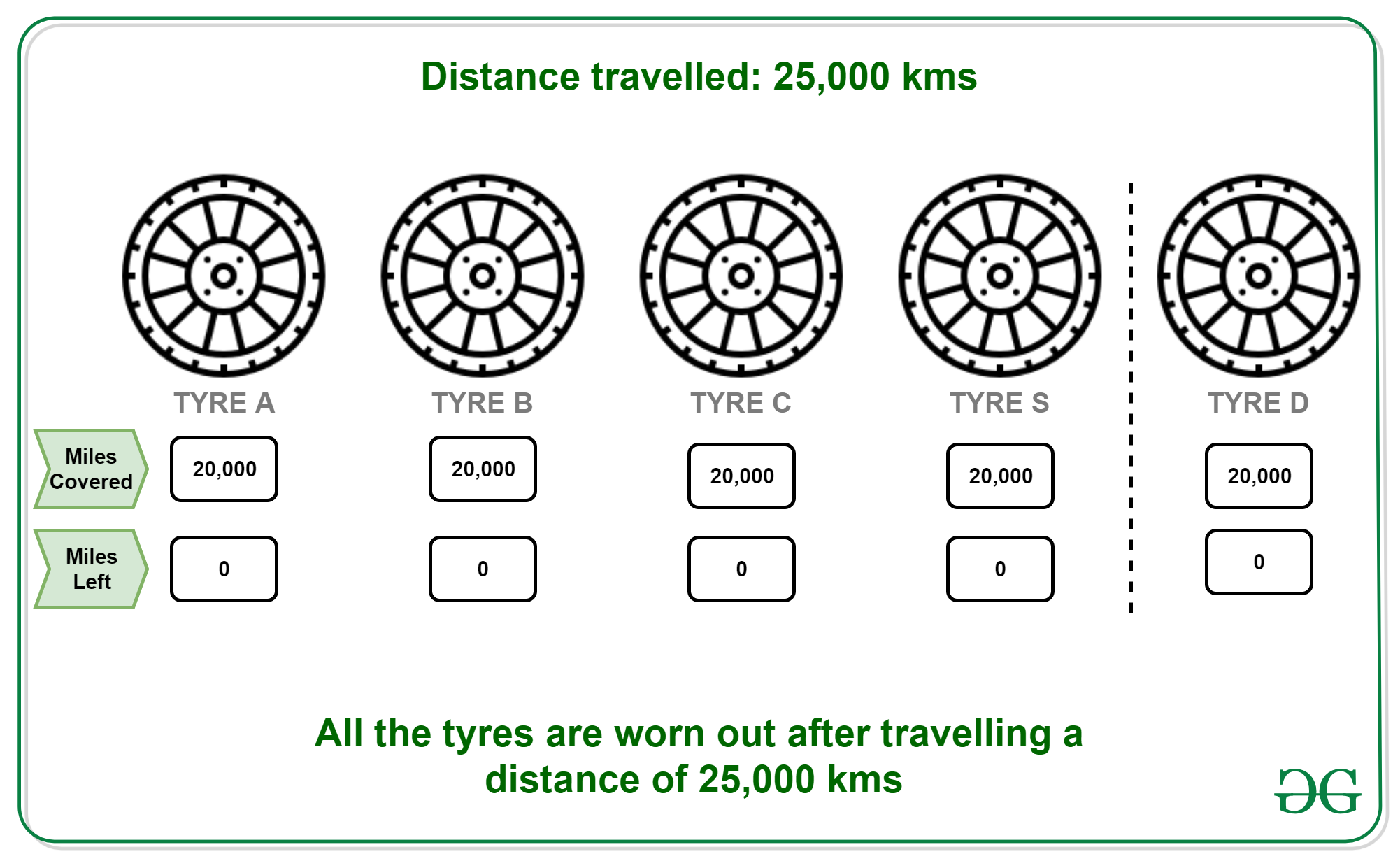
All tyres are used to their full strength.
Related Amazon interview question
There are n pencils, each having l length. Each can write 4 kilometres. After writing 4 kilometres it has l/4 length. One can join 4 pencils which are having l/4 length and can make 1 pencil. One can’t make pencil of pieces if remaining pieces are 3 or 2 or 1 in number but one can include these remaining pieces whenever needed.
Write a relation independent of l, length of the given pencil, for how much one can write from n pencils.
Examples:
Input: 4 Output: 20
Recursive Approach:
Suppose we use 3 pencils that will 12 and generate 3 used pencils, now if the remaining pencils are greater than zero at least 1 unused pencil can be used with those 3 unused to write 4 and that will generate 1 more unused pencil. This will keep repeating.
if(n-3 >= 1){
f(n) = f(n-3) + 12 + 4
}
else{
// Used pencil that cannot be used
f(n) = 4 + 4
}
Below is the implementation of the above approach:
int count(int n) { if (n < 4) { return (n * 4); } else { return (16 + count(n - 3)); } } |
Mathematical Approach O(1):
Above relation can be optimized in O(1)
// x is max no of time we can //subtract 3 without n-3 <= 3 n - 3 + x <= 3 x > (n-3)/3 i.e. n/3 - 1 if it divides exactly else n/3
Below is the implementation of the above approach:
CPP
// C++ program to find relation independent of l // length of the given pencil, for how much one // can write from n pencils. #include <bits/stdc++.h> using namespace std; // Function to find no of pencils int count(int n) { int x = (n / 3) - 1; if (n % 3) { x++; } return (4 * x + 4 * n); } // Driver function int main() { int n = 5; cout << count(n) << endl; } |
Java
// Java program to find relation independent of l // length of the given pencil, for how much one // can write from n pencils. class GFG { // Function to find no of pencils static int count(int n) { int x = (n / 3) - 1; if (n % 3 > 0) { x++; } return (4 * x + 4 * n); } // Driver code public static void main(String[] args) { int n = 5; System.out.print(count(n) +"\n"); } } // This code is contributed by PrinciRaj1992 |
Python3
# Python3 program to find relation independent of l # length of the given pencil, for how much one # can write from n pencils. # Function to find no of pencils def count(n): x = (n // 3) - 1; if (n % 3 > 0): x+=1; return (4 * x + 4 * n); # Driver code if __name__ == '__main__': n = 5; print(count(n)); # This code is contributed by PrinciRaj1992 |
C#
// C# program to find relation independent of l // length of the given pencil, for how much one // can write from n pencils. using System; class GFG { // Function to find no of pencils static int count(int n) { int x = (n / 3) - 1; if (n % 3 > 0) { x++; } return (4 * x + 4 * n); } // Driver code public static void Main(String[] args) { int n = 5; Console.Write(count(n) +"\n"); } } // This code is contributed by 29AjayKumar |
24
