Mid Point Theorem
Last Updated :
12 Feb, 2024
Midpoint theorem states that “The line segment drawn from the midpoint of two sides of the triangle is parallel to the third side and is equal to half of the third side of the triangle. Geometry is an important part of mathematics that deals with different shapes and figures. Triangles are an important part of geometry and the mid-point theorem points towards the midpoints of the triangle.
Midpoint Theorem Definition
Midpoint theorem states that the line segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of the third side. Consider a triangle, ΔABC. Let D and E be the midpoints of AB and AC respectively, now join DE. Then the midpoint theorem states that DE is parallel to BC and equal to half of BC.
Mid-Point Theorem Proof
This theorem states that”
“Line segment joining mid-points of two sides of a triangle is parallel to the third side of the triangle and is half of it”

Given:
A triangle ABC in which D is the mid-point of AB and E is the mid-point of AC.
To Prove:
DE ∥ BC and DE = 1/2(BC)
Construction:
Extend the line segment joining points D and E to F such that DE = EF and join CF.
Proof:
In ∆AED and ∆CEF
DE = EF (construction)
∠1 = ∠2 (vertically opposite angles)
AE = CE (E is the mid-point)
△AED ≅ △CEF by SAS criteria
Therefore,
∠3 =∠4 (c.p.c.t)
But these are alternate interior angles.
So, AB ∥ CF
AD = CF (c.p.c.t)
But AD = DB (D is the mid-point)
Therefore, BD = CF
In BCFD
BD∥ CF (as AB ∥ CF)
BD = CF
BCFD is a parallelogram as one pair of opposite sides is parallel and equal.
Therefore,
DF∥ BC (opposite sides of parallelogram)
DF = BC (opposite sides of parallelogram)
As DF∥ BC, DE∥ BC and DF = BC
But DE = EF
So, DF = 2(DE)
2(DE) = BC
DE = 1/2(BC)
Hence, proved that the line joining the mid-points of two sides of the triangle is parallel to the third side and is half of it.
Converse of Mid-Point Theorem
The line drawn through the mid-point of one side of a triangle parallel to the base of a triangle bisects the third side of the triangle.

Given:
In triangle PQR, S is the mid-point of PQ and ST ∥ QR
To Prove:
T is the mid-point of PR.
Construction:
Draw a line through R parallel to PQ and extend ST to U.
Proof:
ST∥ QR (given)
So, SU∥ QR
PQ∥ RU (construction)
Therefore, SURQ is a parallelogram.
SQ = RU (Opposite sides of parallelogram)
But SQ = PS (S is the mid-point of PQ)
Therefore, RU = PS
In △PST and △RUT
∠1 =∠2 (vertically opposite angles)
∠3 =∠4 (alternate angles)
PS = RU (proved above)
△PST ≅ △RUT by AAS criteria
Therefore, PT = RT
T is the mid-point of PR.
Midpoint of any line segment is defined as the coordinate point that divides the line segment into two equal parts.
Suppose P(x1, y1) and Q(x2, y2) are the coordinates of endpoints of any line segment, then the midpoint formula is given as:
Midpoint = [(x1 + x2)/2, (y1 + y2)/2]
Read More,
Examples on Mid Point Theorem
Example 1: l, m, and n are three parallel lines. p and q are two transversals intersecting parallel lines at A, B, C, D, E, and F as shown in the figure. If AB:BC = 1:1, find the ratio of DE:EF.

Given: AB:BC = 1:1
To find: DE:EF
Construction: Join AF such that it intersects line m at G.
In △ACF
AB = BC (1:1 ratio)
BG∥ CF (as m∥n)
Therefore, by converse of mid-point theorem G is the midpoint of AF (AG = GF)
Now, in △AFD
AG = GF (proved above)
GE∥ AD (as l∥m)
Therefore, by converse of mid-point theorem E is the mid-point of DF (FE = DE)
So, DE:EF = 1:1 (as they are equal)
Example 2: In the figure given below L, M and N are mid-points of side PQ, QR, and PR respectively of triangle PQR.
If PQ = 8cm, QR = 9cm and PR = 6cm. Find the perimeter of the triangle formed by joining L, M, and N.
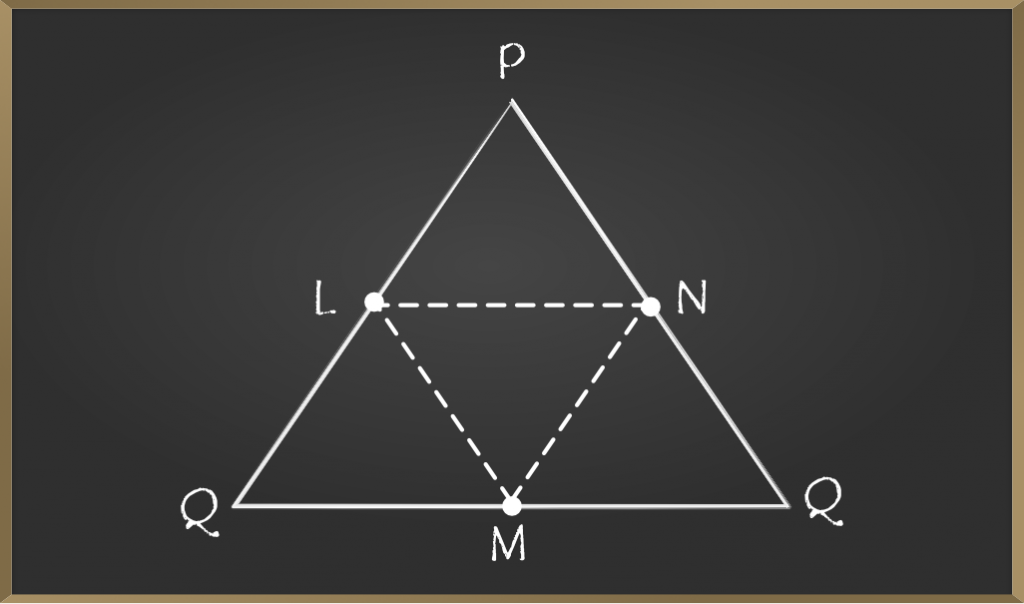
Solution:
As L and N are mid-points
By mid-point theorem
LN ∥ QR and LN = 1/2 × (QR)
LN = 1/2 × 9 = 4.5cm
Similarly, LM = 1/2 × (PR) = 1/2×(6) = 3cm
Similarly, MN = 1/2 × (PQ) = 1/2 × (8) = 4cm
Therefore,
Perimeter of △LMN = LM + MN + LN
Perimeter of △LMN = 3 + 4 + 4.5 = 11.5 cm
Perimeter is 11.5cm
FAQs on MidPoint Theorem
What is Meant by Midpoint Theorem?
Midpoint theorem states that “The line joining the midpoint of two sides of the triangle is parallel to its third side of the triangle and is also half of it.”
What is Converse of Midpoint Theorem?
Converse of mid point theorem states that,” The line drawn through the midpoint of any one side of a triangle, and parallel to another side bisects the third side.
What is Definition of a Midpoint?
Midpoint is defined as the point that divides any line segment into two equal parts.
Share your thoughts in the comments
Please Login to comment...