Number System is a method of representing numbers on the number line with the help of a set of Symbols and rules. These symbols range from 0-9 and are termed as digits. Let’s learn about the number system in detail, including its types, and conversion.
Number System in Maths
Number system in Maths is a writing system for expressing numbers. It is a mathematical notation for representing numbers of a given set, consistently using digits or other symbols. It allows us to perform arithmetic operations like addition, subtraction, multiplication, and division.
Types of Number System
Based on the base value and the number of allowed digits, number systems are of many types.
The four common types of Number System are:
- Decimal Number System
- Binary Number System
- Octal Number System
- Hexadecimal Number System

Decimal Number System
Number system with base value 10 is termed as Decimal number system. It uses 10 digits i.e. 0-9 for the creation of numbers.
Here, each digit in the number is at a specific place with place value a product of different powers of 10. The place value is termed from right to left as first place value called units, second to the left as Tens, so on Hundreds, Thousands, etc. Here, units has the place value as 100, tens has the place value as 101, hundreds as 102, thousands as 103, and so on.
For example: 10285 has place values as
(1 × 104) + (0 × 103) + (2 × 102) + (8 × 101) + (5 × 100)
1 × 10000 + 0 × 1000 + 2 × 100 + 8 × 10 + 5 × 1
10000 + 0 + 200 + 80 + 5
10285
Read More:
Binary Number System
Number System with base value 2 is termed as Binary number system. It uses 2 digits i.e. 0 and 1 for the creation of numbers. The numbers formed using these two digits are termed as Binary Numbers.
Binary number system is very useful in electronic devices and computer systems because it can be easily performed using just two states ON and OFF i.e. 0 and 1.
Decimal Numbers 0-9 are represented in binary as: 0, 1, 10, 11, 100, 101, 110, 111, 1000, and 1001
Examples:
14 can be written as 1110
19 can be written as 10011
50 can be written as 110010
Learn More:
Octal Number System
Octal Number System is one in which the base value is 8. It uses 8 digits i.e. 0-7 for creation of Octal Numbers. Octal Numbers can be converted to Decimal value by multiplying each digit with the place value and then adding the result. Here the place values are 80, 81, and 82. Octal Numbers are useful for the representation of UTF8 Numbers.
Example:
(135)10 can be written as (207)8
(215)10 can be written as (327)8
Hexadecimal Number System
Number System with base value 16 is termed as Hexadecimal Number System. It uses 16 digits for the creation of its numbers. Digits from 0-9 are taken like the digits in the decimal number system but the digits from 10-15 are represented as A-F i.e. 10 is represented as A, 11 as B, 12 as C, 13 as D, 14 as E, and 15 as F. Hexadecimal Numbers are useful for handling memory address locations.
Examples:
(255)10 can be written as (FF)16
(1096)10 can be written as (448)16
(4090)10 can be written as (FFA)16
Learn More:
Conversion of Number Systems
Conversion between numbers systems is quite an easy task. These are the types of conversions that happen from one number system to another:
- Decimal to Other Number Systems
- Binary to Other Number Systems
- Octal to Other Number Systems
- Hexadecimal to Other Number Systems
Let’s discuss them in detail.
Conversion from Decimal to Other Number Systems
Decimal Numbers are represented with digits 0-9 and with base 10. Conversion of a number system means conversion from one base to another. Following are the conversion of the Decimal Number System to other Number Systems:
Decimal to Binary Conversion
Decimal numbers are represented in base 10, but the binary numbers are of base 2. Hence, to convert a decimal number to binary number, the base of that number is to be changed. Follow the steps given below:
- Step 1: Divide the Decimal Number with the base of the number system to be converted to. Here the conversion is to binary, hence the divisor will be 2.
- Step 2: The remainder obtained from the division will become the least significant digit of the new number.
- Step 3: The quotient obtained from the division will become the next dividend and will be divided by base i.e. 2.
- Step 4: The remainder obtained will become the second least significant digit i.e. it will be added in the left of the previously obtained digit.
Now, the steps 3 and 4 are repeated until the quotient obtained becomes 0, and the remainders obtained after each iteration are added to the left of the existing digits.
After all the iterations are over, the last obtained remainder will be termed as the Most Significant digit.

Decimal to Octal Conversion
Octal Numbers are represented in base 8. Hence, to convert a decimal number to octal number, the base of that number is to be changed. Follow the steps given below:
- Step 1: Divide the Decimal Number with the base of the number system to be converted to. Here the conversion is to octal, hence the divisor will be 8.
- Step 2: The remainder obtained from the division will become the least significant digit of the new number.
- Step 3: The quotient obtained from the division will become the next dividend and will be divided by base i.e. 8.
- Step 4: The remainder obtained will become the second least significant digit i.e. it will be added in the left of the previously obtained digit.
Now, the steps 3 and 4 are repeated until the quotient obtained becomes 0, and the remainders obtained after each iteration are added to the left of the existing digits.

Decimal to Hexadecimal Conversion
Hexadecimal Numbers are represented in base 16. Hence, to convert a decimal number to hexadecimal number, the base of that number is to be changed. Follow the steps given below:
- Step 1: Divide the Decimal Number with the base of the number system to be converted to. Here the conversion is to Hex hence the divisor will be 16.
- Step 2: The remainder obtained from the division will become the least significant digit of the new number.
- Step 3: The quotient obtained from the division will become the next dividend and will be divided by base i.e. 16.
- Step 4: The remainder obtained will become the second least significant digit i.e. it will be added in the left of the previously obtained digit.
Now, the steps 3 and 4 are repeated until the quotient obtained becomes 0, and the remainders obtained after each iteration are added to the left of the existing digits.

Conversion from Binary to Other Number Systems
Binary Numbers are represented with digits 0 and 1 and with base 2. Conversion of a number system means conversion from one base to another. Following are the conversion of the Binary Number System to other Number Systems:
Binary to Decimal Conversion
Binary numbers are represented in base 2 but the decimal numbers are of base 10. Hence, to convert the binary number into a decimal number, the base of that number is to be changed. Follow the steps given below:
- Step 1: Multiply each digit of the Binary number with the place value of that digit, starting from right to left i.e. from LSB to MSB.
- Step 2: Add the result of this multiplication and the decimal number will be formed.
Example: To convert (11101011)2 into a decimal number

Binary to Octal Conversion
Binary numbers are represented in base 2 but the octal numbers are of base 8. Hence, to convert the binary number into octal number, the base of that number is to be changed. Follow the steps given below:
- Step 1: Divide the binary number into groups of three digits starting from right to left i.e. from LSB to MSB.
- Step 2: Convert these groups into equivalent octal digits.
Example: To convert (11101011)2 into an octal number

Binary to Hexadecimal Conversion
Binary numbers are represented in base 2 but the Hexadecimal numbers are of base 10. Hence, to convert the binary number into Hex number, the base of that number is to be changed. Follow the steps given below:
- Step 1: Divide the binary number into groups of four digits starting from right to left i.e. from LSB to MSB.
- Step 2: Convert these groups into equivalent hex digits.
Example: To convert (1110101101101)2 into a hex number

Conversion from Octal to Other Number Systems
Octal Numbers are represented with digits 0-7 and with base 8. Conversion of a number system means conversion from one base to another. Following are the conversions of the Octal Number System to other Number Systems:
Octal to Decimal Conversion:
Octal numbers are represented in base 8, but the decimal numbers are of base 10. Hence, to convert an octal number to a decimal number, the base of that number is to be changed. Follow the steps given below:
Step 1: Multiply each digit of the Octal number with the place value of that digit, starting from right to left i.e. from LSB to MSB.
Step 2: Add the result of this multiplication and the decimal number will be formed.
Let’s see an example.

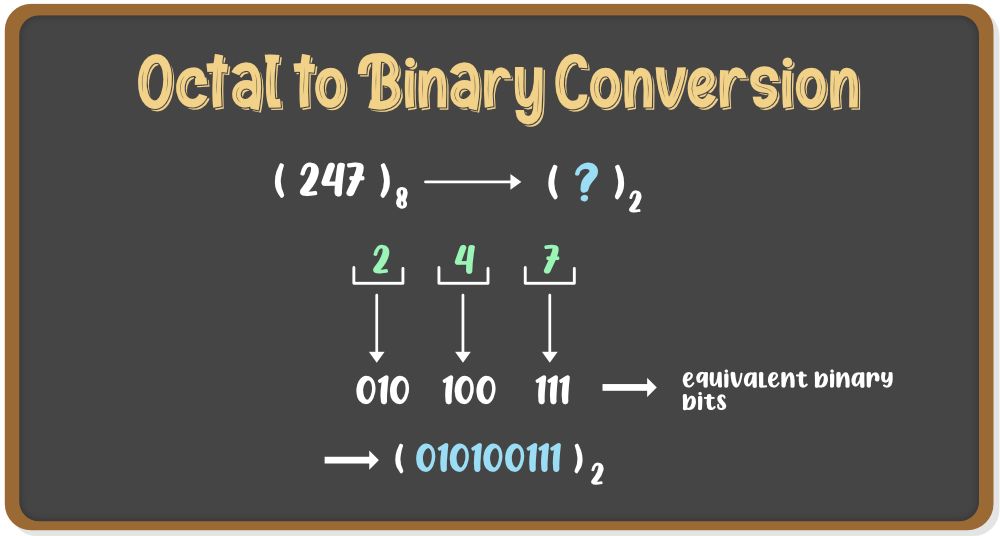
Octal to Binary Conversion:
Octal numbers are represented in base 8, but the binary numbers are of base 2. Hence, to convert an octal number to a binary number, the base of that number is to be changed. Follow the steps given below:
- Step 1: Write each digit of the octal number separately.
- Step 2: Convert each digit into an equivalent group of three binary digits.
- Step 3: Combine these groups to form the whole binary number.
Example: (247)8 is to be converted to binary
Octal to Hexadecimal Conversion:
Octal numbers are represented in base 8, but the hexadecimal numbers are of base 16. Hence, to convert an octal number to a hex number, the base of that number is to be changed. Follow the steps given below:
- Step 1: We need to convert the Octal number to Binary first. For that, follow the steps given in the above conversion.
- Step 2: Now to convert the binary number to Hex number, divide the binary digits into groups of four digits starting from right to left i.e. from LSB to MSB.
- Step 3: Add zeros prior to MSB to make it a proper group of four digits(if required)
- Step 4: Now convert these groups into their relevant decimal values.
- Step 5: For values from 10-15, convert it into Hex symbols i.e from A-F
Example: (5456)8 is to be converted to hex

Conversion from Hexadecimal to Other Number Systems
Hex Numbers are represented with digits 0-9 and with letters A-F and with base 16. Conversion of a number system means conversion from one base to another. Following are the conversions of the Hexadecimal Number System to other Number Systems:
Hexadecimal to Decimal Conversion:
Hexadecimal numbers are represented in base 16 but the decimal numbers are of base 10. Hence, to convert a hexadecimal number to a decimal number, the base of that number is to be changed. Follow the steps given below:
- Step 1: Write the decimal values of the symbols used in the Hex number i.e. from A-F
- Step 2: Multiply each digit of the Hex number with its place value. starting from right to left i.e. LSB to MSB.
- Step 3: Add the result of multiplications and the final sum will be the decimal number.
Example: To convert (8EB4)16 into a decimal value

Hexadecimal to Binary Conversion
Hex numbers are represented in base 16, but the binary numbers are of base 2. Hence, to convert a hexadecimal number to a binary number, the base of that number is to be changed. Follow the steps given below:
- Step 1: Convert the Hex symbols into its equivalent decimal values.
- Step 2: Write each digit of the Hexadecimal number separately.
- Step 3: Convert each digit into an equivalent group of four binary digits.
- Step 4: Combine these groups to form the whole binary number.
Example: (B2E)16 is to be converted to binary

Hexadecimal to Octal Conversion:
Hexadecimal numbers are represented in base 16, but the octal numbers are of base 8. Hence, to convert a hex number to an octal number, the base of that number is to be changed. Follow the steps given below:
- Step 1: We need to convert the Hexadecimal number to Binary first. For that, follow the steps given in the above conversion.
- Step 2: Now to convert the binary number to Octal number, divide the binary digits into groups of three digits starting from right to left i.e. from LSB to MSB.
- Step 3: Add zeros prior to MSB to make it a proper group of three digits(if required)
- Step 4: Now convert these groups into their relevant decimal values.
Example: (B2E)16 is to be converted to hex

Read More:
FAQs on Number System in Maths
What are Number Systems with Examples?
Number systems are methods of representing numbers using symbols or digits. Here are the number systems with examples:
- Decimal (Base-10): Uses digits 0-9. Example: 456.
- Binary (Base-2): Uses digits 0 and 1. Example: 1010.
- Octal (Base-8): Uses digits 0-7. Example: 64.
- Hexadecimal (Base-16): Uses digits 0-9 and letters A-F. Example: 1A3.
- Roman Numerals: Uses letters to represent values. Example: IX, XIV, CXXV.
What are Different Types of Number Systems?
There are several types of number systems, each with its own base and representation. Here are the main ones:
- Decimal Number System (Base-10): Uses digits 0 through 9, with each place value representing a power of 10.
- Binary Number System (Base-2): Uses digits 0 and 1, with each place value representing a power of 2.
- Octal Number System (Base-8): Uses digits 0 through 7, with each place value representing a power of 8.
- Hexadecimal Number System (Base-16): Uses digits 0 through 9 and letters A through F (representing values 10 through 15), with each place value representing a power of 16.
- Roman Numeral System: Uses specific letters to represent values, with various rules for addition and subtraction.
What are Conversion Rules of Number Systems?
Here are the conversion rules for common number systems:
- Decimal to Binary:
- Divide the decimal number by 2.
- Write down the remainder.
- Repeat the process with the quotient until it becomes 0.
- The binary equivalent is obtained by reading the remainders in reverse order.
- Binary to Decimal:
- Write down the binary number.
- Assign each digit a place value, starting from the rightmost digit (1, 2, 4, 8, …).
- Multiply each digit by its corresponding place value.
- Add up all the products to get the decimal equivalent.
- Decimal to Octal:
- Divide the decimal number by 8.
- Write down the remainder.
- Repeat the process with the quotient until it becomes 0.
- The octal equivalent is obtained by reading the remainders in reverse order.
- Octal to Decimal:
- Write down the octal number.
- Assign each digit a place value, starting from the rightmost digit (1, 8, 64, …).
- Multiply each digit by its corresponding place value.
- Add up all the products to get the decimal equivalent.
- Decimal to Hexadecimal:
- Divide the decimal number by 16.
- Write down the remainder.
- Repeat the process with the quotient until it becomes 0.
- For remainders greater than 9, represent them with corresponding hexadecimal letters (A for 10, B for 11, etc.).
- The hexadecimal equivalent is obtained by reading the remainders in reverse order.
- Hexadecimal to Decimal:
- Write down the hexadecimal number.
- Assign each digit a place value, starting from the rightmost digit (1, 16, 256, …).
- Multiply each digit by its corresponding place value.
- Add up all the products to get the decimal equivalent.
Share your thoughts in the comments
Please Login to comment...