Quadrilateral is a type of polygon that has four sides, four vertices, and four angles, along with a pair of diagonals. The sum of its interior angles is 360°. Let’s learn what is a quadrilateral, its types, properties, and examples in detail.

Illustration of a Quadrilateral
What are Quadrilateral?
A quadrilateral is a shape with four sides, four corners, and four angles. No matter what type of quadrilateral it is, the total of all its inside angles always adds up to 360 degrees. Examples of quadrilaterals include squares, rectangles, parallelograms, rhombuses, trapezoids, and kites. Each type has its own special features and properties but they all are four-sided figures.
Quadrilateral Definition
A quadrilateral is defined as a polygon having 4 sides, 4 angles, and 4 vertices. The quadrilateral is a type of polygon in which the sides are defined in a proper pattern.
For example, in the diagram below, the quadrilateral can be defined as ABCD, ADCB, BCDA, CDAB, etc. It cannot be defined as ACBD or BDAC. Here, the quadrilateral’s sides are AB, BC, CD, and DA, and the diagonals are AC and BD.
Properties of Quadrilateral
The properties of a quadrilateral are:
- A quadrilateral has 4 sides.
- It has 4 vertices.
- It has 4 angles.
- It has 2 diagonals.
- The sum of its internal angles is 360°.
Types of Quadrilateral
Based on their properties, quadrilaterals are divided into two major types:
- Convex quadrilaterals and
- Concave quadrilaterals.
These concave and convex quadrilaterals can be further classified into their subdivisions.

Shape of Different Quadrilaterals
Concave Quadrilateral
Quadrilaterals that have one interior angle greater than 180° and one diagonal lies outside the quadrilateral are called concave quadrilaterals.
One of the examples of a concave quadrilateral is a Dart. It is a quadrilateral with bilateral symmetry like a kite, but with a reflex interior angle.

Diagram of a Dart
Here, in the image given below, one of the interior angles of the quadrilateral is 210°, which is greater than 180°. Therefore, the quadrilateral is a concave quadrilateral.
Convex Quadrilateral
Quadrilaterals that have all four interior angles less than 180° are called concave quadrilaterals.
There are various types of Convex Quadrilaterals, which are :
- Trapezium
- Kite
- Parallelogram
- Rectangle
- Rhombus
- Square

Convex Quadrilateral
Equilateral Quadrilateral vs Irregular Quadrilaterals
Equilateral Quadrilateral and Irregular Quadrilaterals are two distinct types of quadrilaterals with unique characteristics and properties.
Equilateral Quadrilateral
- An equilateral quadrilateral, also known as a square, is a special type of quadrilateral where all four sides are equal in length.
- Additionally, all interior angles of an equilateral quadrilateral are right angles, meaning they each measure 90 degrees.
- Due to its symmetrical nature, an equilateral quadrilateral exhibits properties such as equal diagonals, congruent adjacent sides, and perpendicular bisectors that divide the figure into congruent right triangles.
- Squares are highly symmetrical and possess properties ideal for various applications, including in architecture, engineering, and mathematics.
Irregular Quadrilaterals
- Irregular quadrilaterals encompass a broad category of quadrilaterals that do not have all sides equal in length or all angles equal in measure.
- Examples of irregular quadrilaterals include rectangles, parallelograms, rhombuses, trapezoids, and kites, among others.
- Unlike equilateral quadrilaterals, irregular quadrilaterals do not have consistent properties regarding side lengths and angles.
- The properties of irregular quadrilaterals vary depending on their specific geometric characteristics. For instance, rectangles have opposite sides that are equal in length and all interior angles are right angles, while parallelograms have opposite sides that are equal in length and opposite angles that are equal in measure.
- Irregular quadrilaterals are encountered in everyday life and have diverse applications in fields such as architecture, design, and art.
Shapes of Quadrilaterals
Quadrilaterals exhibit diverse shapes, ranging from the symmetrical squares and rectangles to the more complex and irregular parallelograms and trapezoids.
Trapezium
A trapezium is a quadrilateral that has one pair of opposite sides parallel. In a regular trapezium, non-parallel sides are equal, and its base angles are equal.
The area of trapezium is 1/2 × Sum of parallel sides × Distance between them.

Trapezium Illustration
Properties of Trapezium
Here are two important properties of a trapezium:
- The sides of the trapezium that are parallel to each other are known as the bases of trapezium. In the above image, AB and CD are the base of the trapezium.
- The sides of the trapezium that are non-parallel are called the legs. In the above image, AD and BC are the legs.
Area of Trapezium
The area of a trapezium can be calculated using the formula:
Area =1/2 × (a+b) × (h)
Where the parallel sides (a and b) are the two sides of the trapezium that are parallel to each other, and the height (h) is the perpendicular distance between these parallel sides.
Perimeter of Trapezium
The perimeter of a trapezium is the sum of the lengths of all its four sides.
If the trapezium has side lengths a, b, c, and d, then the perimeter is:
Perimeter = a+b+c+d
Kite
Kite has two pairs of equal adjacent sides and one pair of opposite angles equal. Diagonals of kites intersect perpendicularly.
The longest diagonal of the kite bisects the smaller one.

Kite Illustration
Properties of Kite
Let’s discuss some of the properties of a kite.
- A kite has two pairs of equal adjacent sides. For example, AC = BC and AD = BD.
- The interior opposite angles that are obtuse are equal; here, ∠A = ∠B.
- The diagonals of a kite are perpendicular to each other; here, AB is perpendicular to CD.
- The longer diagonal of the kite bisects the shorter diagonal. Here, CD bisects AB.
Area of a Kite
The area of a kite is calculated using the formula:
Area = ½ (d1 x d2)
where, d1 and d2 represent the lengths of the diagonals of the kite.
It’s important to note that this formula works regardless of whether d1 is longer or shorter than d2.
Perimeter of a Kite
The perimeter of a kite, which is the total length of all its sides added together, is calculated using the formula:
Perimeter = 2(a + b)
where, a and b represent the lengths of the two pairs of equal sides of the kite.
Parallelogram
Parallelogram is a quadrilateral whose opposite sides are equal and parallel. Opposite angles of a Parallelogram are equal, and its diagonals bisect each other.

Parallelogram Illustration
Properties of Parallelogram
The properties of a Parallelogram are:
- The opposite sides of a parallelogram are parallel and equal. In the above example, AB and CD are parallel and equal, and AC and BD are parallel and equal.
- The opposite angles in a parallelogram are equal. ∠A = ∠D and ∠B = ∠C.
- The diagonals of a parallelogram bisect each other.
Area of a Parallelogram
The area of a parallelogram is calculated as the product of its base and height. The formula is given as:
Area of Parallelogram = base × height
Where the base is any one of the parallel sides, and the height is the perpendicular distance between the base and its opposite side.
Perimeter of a Parallelogram
The perimeter of a parallelogram is the sum of the lengths of all its sides. Since opposite sides of a parallelogram are equal in length, the perimeter is calculated as:
Perimeter of Parallelogram = 2 × (a+b)
Where, a and b are the adjacent sides of a parallelogram.
Rectangle
Rectangle is a quadrilateral whose opposite sides are equal and parallel and all the interior angles equal to 90°.
Diagonals of a rectangle bisect each other.

Illustration of a Rectangle
Note that all the rectangles are parallelograms, but the reverse of this is not true.
Rectangle Properties
These are some of the important properties of rectangle:
- The opposite sides of a rectangle are parallel and equal. In the above example, AB and CD are parallel and equal, and AC and BD are parallel and equal.
- All 4 angles of a rectangle are equal and are equal to 90°. ∠A = ∠B = ∠C = ∠D = 90°.
- The diagonals of a rectangle bisect each other and the diagonals of a rectangle are equal, here, AD = BC.
Area of a Rectangle
The area of a rectangle is calculated as the product of its length and width. The formula is given as:
Area of Rectangle = length × width
Where the length is the longer side and the width is the shorter side of the rectangle.
Perimeter of a Rectangle
The perimeter of a rectangle is the sum of the lengths of all its sides. Since opposite sides of a rectangle are equal in length, the perimeter is calculated as:
Perimeter of Rectangle = 2 × (length + width)
This formula doubles the sum of the length and width because each side is counted twice.
Rhombus
Rhombus is a quadrilateral that has all sides equal and opposite sides parallel. Opposite angles of a rhombus are equal, and diagonals of the Rhombus bisect each other perpendicularly. .
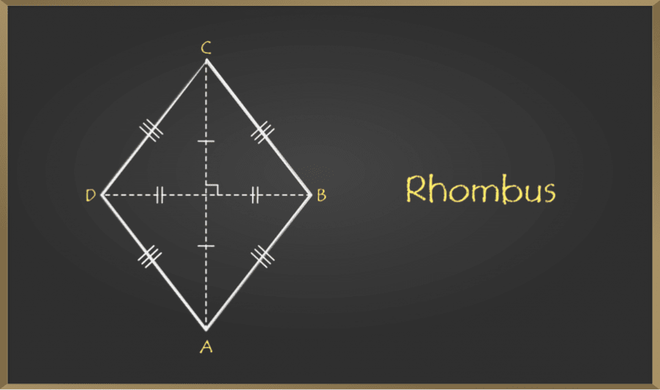
Rhombus Diagram
Note all rhombus are parallelograms, but the reverse of this is not true.
Properties of Rhombus
Here are some of the key properties of a Rhombus:
- All 4 sides of a rhombus are equal. AB = BC = CD = AD.
- The opposite sides of a rhombus are parallel and equal. In the image above, AB is parallel to CD and AD is parallel to BC.
- The diagonals of a rhombus Bisect each other at 90°.
Area of a Rhombus
The area of a rhombus can be calculated by multiplying the lengths of its two diagonals and dividing by 2. The formula is:
Area of Rhombus = 1/2 × (diagonal1 × diagonal2)
Where, diagonal1 and diagonal2 are the lengths of the two diagonals.
Perimeter of a Rhombus
The perimeter of a rhombus is the sum of the lengths of all its four sides. Since all sides of a rhombus are equal in length, the perimeter can be calculated as:
Perimeter of Rhombus = 4 × side
Where sideside is the length of any one of the sides.
Square
A quadrilateral that has all sides equal and opposite sides parallel and all interior angles equal to 90° is called a Diagonals of squares bisect each other perpendicularly. Note that all squares are rhombus but not vice-versa.

Properties of Square
The properties of a square are:
- All four sides of a square are equal to each other.
- The interior angles of a square are 90°.
- The diagonal of a square bisects each other at 90°.
- The opposite sides are parallel, and the adjacent sides are perpendicular in a square.
Area of a Square
The area of a square is calculated by squaring the length of one of its sides. The formula is:
Area of Square = side2
Where sideside is the length of one side of the square.
Perimeter of a Square
The perimeter of a square is the sum of the lengths of all its sides. Since all sides of a square are equal in length, the perimeter can be calculated as:
Perimeter of Square = 4 × side
Where sideside is the length of any one of the sides.
Quadrilateral Theorems
- Sum of Interior Angles Theorem: In any quadrilateral, the sum of the measures of its interior angles equals 360 degrees.
- Opposite Angles Theorem: Within a quadrilateral, the sum of the measures of two opposite angles is 180 degrees.
- Consecutive Angles Theorem: Adjacent (consecutive) angles in a quadrilateral are supplementary, meaning their measures sum up to 180 degrees.
- Diagonals of Parallelograms Theorem: The diagonals of a parallelogram bisect each other, dividing each diagonal into two equal segments.
- Opposite Sides and Angles of Parallelograms Theorem: In a parallelogram, opposite sides are equal in length, and opposite angles are congruent.
- Diagonals of Rectangles and Rhombuses Theorem: In rectangles and rhombuses, the diagonals are equal in length. Additionally, the diagonals of a rectangle are congruent, while those of a rhombus bisect each other at right angles.
- Diagonals of Trapezoids Theorem: The diagonals of a trapezoid may have different lengths. However, the segment joining the midpoints of the non-parallel sides is parallel to the bases and is equal to half their sum.
Quadrilateral Lines of Symmetry
A quadrilateral has lines of symmetry that are imaginary lines that pass through the center of the quadrilateral and divide it into two similar halves. A line of symmetry can:
- Match two vertices on one side of the line with two vertices on the other.
- Pass through two vertices, and the other two vertices pair up when folded over the line.
A regular quadrilateral has four lines of symmetry. For example, a square has four lines of symmetry, including both its diagonals and the lines joining the midpoints of its opposite sides. A rectangle has two lines of symmetry, including the lines joining the midpoint of the opposite and parallel lines.
Quadrilateral Sides and Angles
The following table illustrates how the sides and angles of quadrilaterals make them different from one another:
|
Characteristics of Quadrilaterals
|
| Sides and angles |
Square |
Rectangle |
Rhombus |
Parallelogram |
Trapezium |
| All sides are equal |
Yes |
No |
Yes |
No |
No |
| Opposite sides are parallel |
Yes |
Yes |
Yes |
Yes |
Yes |
| Opposite sides are equal |
Yes |
Yes |
Yes |
Yes |
No |
| All the angles are of the same measure |
Yes |
Yes |
No |
No |
No |
| Opposite angles are of equal measure |
Yes |
Yes |
Yes |
Yes |
No |
| Diagonals bisect each other |
Yes |
Yes |
Yes |
Yes |
No |
| Two adjacent angles are supplementary |
Yes |
Yes |
Yes |
Yes |
No |
The two basic formulas for quadrilaterals, are:
- Area of Quadrilateral
- Perimeter of Quadrilateral
Let’s discuss them in detail.
Area of Quadrilateral
The area of a quadrilateral is defined as the amount of space covered by a quadrilateral in a two-dimensional space. The different types of quadrilaterals have different formulae for their respective area.
The chart given below shows the formula for the area of each type of quadrilateral:

Perimeter of Quadrilateral
The perimeter of a quadrilateral is the sum of all its sides. For different quadrilateral shapes, the perimeter formula is different as they portray different characteristics.
Below are the formulas for different quadrilateral shapes.
|
Perimeter Formula of Quadrilaterals
|
| Quadrilateral Shape |
Perimeter Formula |
| Parallelogram |
2 (Base + Side) |
| Rectangle |
2 (Length + Breadth) |
| Rhombus |
4 × Side |
| Square |
4 × Side |
| Kite |
2 (a + b), where a and b are adjacent pairs. |
Difference between Different Quadrilaterals
Square vs Rhombus
A square is a special type of rhombus where all angles are right angles and all sides are equal.
Square vs Rectangle
While both have opposite sides equal and all angles as right angles, squares have equal sides, while rectangles may have unequal sides.
Rectangle vs Parallelogram
Rectangles have all angles as right angles, unlike parallelograms which may not, but both have opposite sides equal.
Rhombus vs Kite
A rhombus has all sides equal, whereas a kite typically has two pairs of adjacent sides equal.
Rhombus vs Trapezium
Rhombuses have all sides equal, while trapeziums have one pair of parallel sides.
Rhombus vs Diamond
A diamond, when referred to geometrically, essentially represents a rhombus, sharing the same properties of equal sides and opposite angles.
Solved Questions on Quadrilateral
Here are some solved examples on quadrilaterals for your help.
Question 1: The perimeter of quadrilateral ABCD is 46 units. AB = x + 7, BC = 2x + 3, CD = 3x – 8, and DA = 4x – 6. Find the length of the shortest side of the quadrilateral.
Solution:
Perimeter = Sum of all sides
= 46 = 10x – 4 or [x = 5]
That gives, AB = 12 units, BC = 13 units, CD = 7 units, DC = 14 units
Hence, length of shortest side is 7 units (i.e. CD).
Question 2: Given a trapezoid ABCD (AB || DC) with median EF. AB = 3x – 5, CD = 2x -1 and EF = 2x + 1. Find the value of EF.
Solution:
We know that the Median of the trapezoid is half the sum of its bases.
= EF = (AB + CD) / 2
= 4x + 2 = 5x – 6 or [x = 8]
Therefore EF = 2x + 1 = 2(8) + 1 => EF = 17 units.
Question 3: In a Parallelogram, adjacent angles are in the ratio of 1:2. Find the measures of all angles of this Parallelogram.
Solution:
Let the adjacent angle be x and 2x.
We know that in of a Parallelogram adjacent angles are supplementary.

= x + 2x = 180° or [x = 60°]
Also, opposite angles are equal in a Parallelogram.
Therefore measures of each angles are 60°, 120°, 60°, 120°.
FAQs on Quadrilateral
What is Quadrilateral?
A quadrilateral can be defined as a type of polygon that has four sides, four vertices, and four angles along with a pair of diagonals. The Sum of interior angles of a quadrilateral is 360°.
How Many Types of Quadrilateral are there?
Here are the main types of quadrilaterals:
- Square: All sides are equal, and all angles are right angles (90 degrees).
- Rectangle: Opposite sides are equal and parallel, and all angles are right angles.
- Rhombus: All sides are equal, but angles are not necessarily right angles. Opposite angles are equal, and opposite sides are parallel.
- Parallelogram: Opposite sides are equal and parallel. Opposite angles are equal, but not all angles have to be right angles.
- Trapezium : At least one pair of opposite sides is parallel. A trapezium has at least one pair of parallel sides.
- Kite: Two pairs of adjacent sides are of equal length. One diagonal bisects the other at right angles.
What is the Sum of Interior Angles of Quadrilateral?
The sum of the interior angles of a quadrilateral is 360°. The same case applies to all quadrilateral shapes.
How To Find the Area of Quadrilateral?
The area of a quadrilateral is defined as the space covered by the quadrilateral shape in 2-dimensional space. The different types of quadrilateral have different formula for area according to their properties. For example, the area of square is a2 where, a is the side length, the area of rectangle is l × b, where l and b are the length and breadth respectively, etc.
What is Cyclic Quadrilateral?
A cyclic quadrilateral is defined as that quadrilateral in which all the four vertices of the quadrilateral lie on the circumference of a circle.
What are Properties of Quadrilateral?
Here are the key properties of a quadrilateral:
- Four Sides: By definition, all quadrilaterals have four straight sides.
- Four Vertices: The points where the sides meet are called vertices, and quadrilaterals have four of these.
- Four Angles: There are four interior angles in a quadrilateral.
- Sum of Interior Angles: The sum of the interior angles in any quadrilateral is 360 degrees.
- Two Diagonals: Quadrilaterals have two diagonals, which are segments connecting opposite vertices.
Explain the Golden Quadrilateral.
Golden quadrilateral is the famous term given to the national highway that connects the major states and the industrial, agriculateral, and cultural centres of India. On the map, the shape of the highway is the shape of a quadrilateral.
Which Quadrilateral is not a Parallelogram?
A trapezium is a quadrilateral that is not a parallelogram.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...