While solving and finding the Area of a Triangle, Certain parameters are expected to be provided beforehand, for example, the height and the base of the triangle must be available Or in case of an Equilateral Triangle, the lengths of the side should be given.
Area of triangle is usually given by,
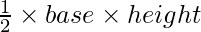
Where base and height are measured from the given triangle. But sometimes it might happen that we don’t have that information. Suppose we only have information about the length of the sides. Height is not known, how will the area be calculated then?
The answer to this question is Heron’s formula.
Heron was born in Egypt in about 10AD. He was a great mathematician, he worked in applied mathematics. His great deal of work revolved around squares, rectangles. This formula is also called “Hero’s Formula”.
Heron’s Formula
Heron’s Formula is also known as Hero’s formula, it is named after a very famous engineer of Egypt, He was famous and known as the “Hero of Alexandria”, His famous works include Heron’s formula, Vending machine, etc. The best part about Heron’s formula was that it did not require any angle or distance prior to solving the area of any Triangle.
Let’s say we have a triangle ABC whose sides are of length “a”, “b” and “c”.
Then the area of that triangle as given by Heron,
Area of triangle ABC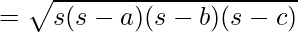
Where a, b and c are the length of the sides and s = semi-perimeter (Half of the perimeter)
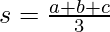
This formula allows us to calculate the area of the triangle where the length of the altitude is not given.
Application of Heron’s Formula in Finding Area of Triangles
Heron’s Formula can be used to find areas of different types of triangles if the length of their sides is given,
Question: Find out the area of the triangle if its sides are 3, 5, 4.
Solution:
Area of this triangle can be calculated by Heron’s formula studied above,
Let’s calculate semi-perimeter first,
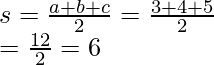
Plugging the values of s, a, b and c in the formula. Let’s calculate the area.
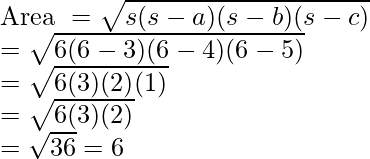
Thus, the area of the triangle is 6 square units.
Application of Heron’s Formula in Finding Area of Quadrilaterals
We know how to calculate the area of standard quadrilaterals like rectangles, squares, and trapeziums. But sometimes it might happen that our quadrilaterals are not in any of these forms.

The quadrilateral given above doesn’t lie in any of these categories, so our standard formulas cannot be used. Heron’s formula helps us in such cases. We can join any two opposite vertices in the above figure and can form two triangles. Then the area can be calculated. Let’s see some examples regarding that.
Question: Find the area of the given rhombus using Heron’s Formula.

Solution:
There are two triangles here, both of them are similar.
The length of sides of both triangles are 100, 100 and 120.
Thus, semi perimeter for both the triangles is,
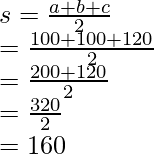
Now, calculating the area of the triangle
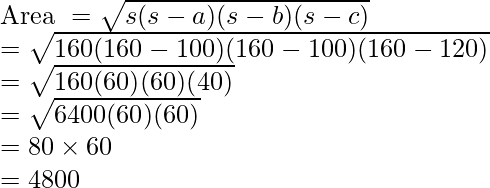
Thus, area of a single triangle is 4800. Since, there are two equal triangles. So, the total area is 9600 sq units.
Let’s see some sample problems on these concepts,
Sample Problems based on Heron’s Formula
Question 1: There is concrete space in the shape of a triangle that needs to be tiled. The cost of tiling is Rs 20 per square unit. Find the total cost of tiling the area.

Answer:
The length of given sides are 10, 10 and 10.
The semi-perimeter “s” = 15
We know the area of the triangle using Heron’s formula.
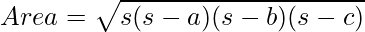
Here, s = 15, a = b = c = 10.
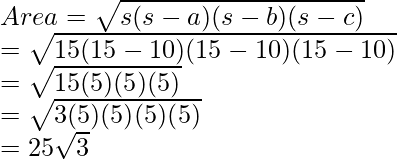
The area of the triangle is 25√3
So, the cost of tiling the area = 25√3 x 20
= 500√3
= 500 (1.73)
= 866 (approx)
Thus, cost of tiling the area is Rs. 866.
Question 2: The length of sides of a triangle is in ratio 3:5:4 and the perimeter is 96m. Find the area of the triangle.
Solution:
The sides are in ratio of 3:5:4. Suppose the length of the sides is 3x,5x and 4x.
3x + 5x + 4x = 96
= 12x = 96
= x = 8.
Thus, the sides are 24, 40, 32. Now let’s calculate “s” and plug in the values in Heron’s formula.
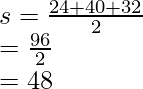

Question 3: Let’s say the sides of the triangle are given as 3y, 4y, and 5y. Find out the expression for the area of the triangle.
Answer:
Let’s find out the perimeter and semi perimeter so that we can plug in the values in Heron’s formula.
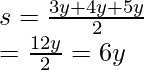
Plugging in the values in Heron’s Formula.
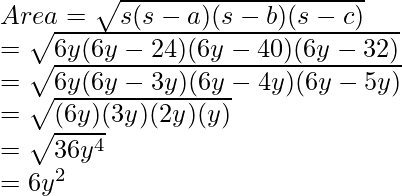
Question 4: Find out the area of the quadrilateral given below:

Solution:
The quadrilateral ABCD can be divided into two triangles whose area we can compute if we join A and C.
Now we have triangles ACD and ABC. Out of which ACD is a right-angled triangle.
AC2 = AD2 + DC2
⇒ AC2 = 92 + 402
⇒ AC2 = 81 + 1600
⇒ AC2 = 1681
⇒ AC = 41
Area of triangle ADC = 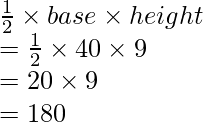
Area of triangle ABC will be calculated using Heron’s Formula. The sides of the triangle are 28,15 and 41.
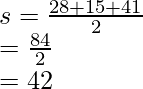
Area of triangle ABC = 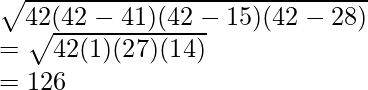
Area of quadrilateral = Area of triangle ADC + Area of triangle ABC
= 180 + 126
= 306 sq units.
Question 5: Let’s assume a triangle whose sides are given as 2y, 2y + 2, and 4y – 2 and its area if given by y√10. Find out the value of y.
Solution:
Let’s calculate “s”
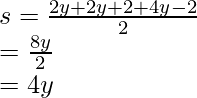
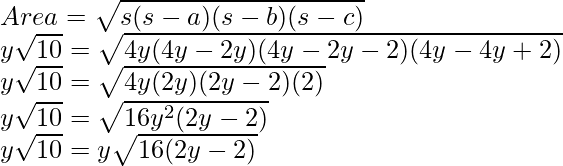
Comparing both sides of the equation,
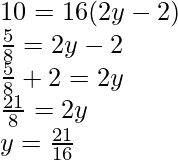
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...