Verifying Inverse Functions by Composition
Last Updated :
16 Jun, 2021
A function can be seen as a mathematical formula or a machine that throws output when an input is given. The output is usually some processed version of the input. Function’s inverses can be seen as the operations which give us the input back on giving them the output. In other words, inverse functions reverse the operations of the function. These concepts are used in a lot of places in mathematics, where we need to determine what was the input for the given output. Let’s see these concepts in detail.
Inverse Functions
Inverse functions in a general sense are the reverse of functions. For a function f(x), its inverse is denoted by f-1(x). The figure denotes how both functions and inverse functions are related to each other. Let’s consider the function f(x) = x + 3, it means that it adds 3 to it’s input. So, it is clear that to reverse this process that is to find the input again from the given output, 3 must be subtracted. So, f-1(x) = x – 3.

Methods to find inverses:
Let’s consider a function f(x), for finding out the inverse function f-1(x).
- Replace f(x) with y.
- Now, replace every x with y and vice-versa.
- Solve the equation formed after step 2 for y.
- Replace y with f-1(x).
This method can be used to calculate the inverse for the majority of the functions.
Question: Find the inverse for f(x) = x2 + 1.
Solution.
For finding out the inverse of this function, same steps will be followed.
f(x) = x2 + 1
⇒ y = x2 + 1
Replacing x with y and vice-versa
⇒x = y2 + 1
⇒ y =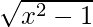
Thus, f-1(x) = 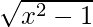
Inverse Composition Rule
Since inverse gives back the input. It is essential to verify whether the inverse that has been calculated is right or not. To do this, we use the property of function composition. Let’s say that f(x) is a function and g(x) is its inverse. The goal is to verify the correctness of the calculated inverse function g(x). Following are the two conditions for verification that g(x) is the inverse of the function f(x):
- f(g(x)) = x for all the x in the domain of g(x).
- g(f(x)) = x for all the x in the domain of f(x).
Since f(x) and g(x) are inverses, their composition in any order creates a function that returns input for input. This function is called the identity function.
Let’s see some problems with these concepts.
Sample Problems
Question 1: Find the inverse of the following function and verify it with the properties mentioned above.
f(x) = 2x + 5
Answer:
Following the steps mentioned in the previous methods.
f(x) = 2x + 5
Replace f(x) with y,
y = 2x + 5
Replace x with y and vice versa
x = 2y + 5
Solving the equation for y,
y = 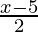
Let the inverse be g(x) = 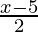 and f(x) = 2x + 5.
and f(x) = 2x + 5.
f(g(x))
f(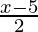 )
)
⇒ 2(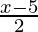 ) + 5
) + 5
⇒x – 5 + 5
⇒x
g(f(x))
g(2x + 5)
⇒ (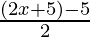 )
)
⇒x
Hence, Verified.
Question 2: Find the inverse of the following function and verify it with the properties mentioned above.
f(x) = x2
Answer:
Following the steps mentioned in the previous methods.
f(x) = x2
Replace f(x) with y,
y = x2
Replace x with y and vice versa
x = y2
Solving the equation for y,
y = √x
Let the inverse be g(x) = √x and f(x) = x2
f(g(x))
f(√x)
⇒ (√x)2
⇒x
g(f(x))
√(x2)
⇒ x
Hence, Verified.
Question 3: Find the inverse of the following function and verify it with the properties mentioned above.
f(x) = 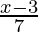
Answer:
Following the steps mentioned in the previous methods.
f(x) =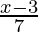
Replace f(x) with y,
y = 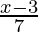
Replace x with y and vice versa
x = 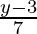
Solving the equation for y,
y = 7x + 3
Let the inverse be g(x) = 7x + 3 and f(x) = 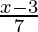
f(g(x))
f(7x + 3)
⇒ 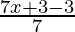
⇒x
g(f(x))
g(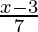 )
)
⇒ 7(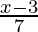 ) + 3
) + 3
⇒x
Hence, Verified.
Question 4: Find the inverse of the following function and verify it with the properties mentioned above.
f(x) = log(x)
Answer:
Following the steps mentioned in the previous methods.
f(x) = log(x)
Replace f(x) with y,
y = log(x)
Replace x with y and vice versa
x = log(y)
Solving the equation for y,
y = ex
Let the inverse be g(x) = ex and f(x) = log(x)
f(g(x))
f(ex)
⇒ log(ex)
⇒x
g(f(x))
⇒elog(x)
⇒ x
Hence, Verified.
Question 5: Find the inverse of the following function and verify it with the properties mentioned above.
f(x) = x3 + 1
Answer:
Following the steps mentioned in the previous methods.
f(x) = x3 + 1
Replace f(x) with y,
y = x3 + 1
Replace x with y and vice versa
x = y3 + 1
Solving the equation for y,
y = ](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1e95db450107054b37c925a29f773ba3_l3.png)
Let the inverse be g(x) = ](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1e95db450107054b37c925a29f773ba3_l3.png) and f(x) = x3 + 1
and f(x) = x3 + 1
f(g(x))
f(](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1e95db450107054b37c925a29f773ba3_l3.png) )
)
⇒ (](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1e95db450107054b37c925a29f773ba3_l3.png) )3 + 1
)3 + 1
⇒x
g(f(x))
⇒![Rendered by QuickLaTeX.com \sqrt[3]{(x^3 + 1) - 1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bdfe8a48f52a74427b3883cc0e7ce391_l3.png)
⇒ x
Hence, Verified.
Question 6: Find the inverse of the following function and verify it with the properties mentioned above.
f(x) = ex + 1
Answer:
Following the steps mentioned in the previous methods.
f(x) = ex + 1
Replace f(x) with y,
y = ex + 1
Replace x with y and vice versa
x = ey + 1
Solving the equation for y,
y = log(x -1)
Let the inverse be g(x) = log(x – 1) and f(x) = ex + 1
f(g(x))
f(log(x – 1))
⇒ elog(x – 1) + 1
⇒x
g(f(x))
⇒ g(ex + 1)
⇒ log(ex + 1 – 1)
⇒ x
Hence, Verified.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...