Gaussian Mixture Model
Last Updated :
10 Jun, 2023
Suppose there are a set of data points that need to be grouped into several parts or clusters based on their similarity. In Machine Learning, this is known as Clustering. There are several methods available for clustering:
In this article, Gaussian Mixture Model will be discussed.
Normal or Gaussian Distribution
In real life, many datasets can be modeled by Gaussian Distribution (Univariate or Multivariate). So it is quite natural and intuitive to assume that the clusters come from different Gaussian Distributions. Or in other words, it tried to model the dataset as a mixture of several Gaussian Distributions. This is the core idea of this model.
In one dimension the probability density function of a Gaussian Distribution is given by
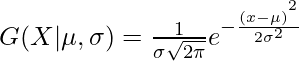
where 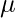 and
and 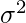 are respectively the mean and variance of the distribution. For Multivariate ( let us say d-variate) Gaussian Distribution, the probability density function is given by
are respectively the mean and variance of the distribution. For Multivariate ( let us say d-variate) Gaussian Distribution, the probability density function is given by
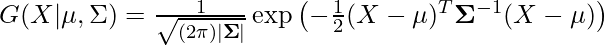
Here 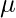 is a d dimensional vector denoting the mean of the distribution and
is a d dimensional vector denoting the mean of the distribution and 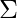 is the d X d covariance matrix.
is the d X d covariance matrix.
Gaussian Mixture Model
Suppose there are K clusters (For the sake of simplicity here it is assumed that the number of clusters is known and it is K). So 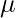 and
and 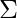 are also estimated for each k. Had it been only one distribution, they would have been estimated by the maximum-likelihood method. But since there are K such clusters and the probability density is defined as a linear function of densities of all these K distributions, i.e.
are also estimated for each k. Had it been only one distribution, they would have been estimated by the maximum-likelihood method. But since there are K such clusters and the probability density is defined as a linear function of densities of all these K distributions, i.e.
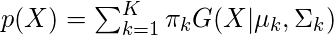
where 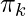 is the mixing coefficient for kth distribution. For estimating the parameters by the maximum log-likelihood method, compute p(X|
is the mixing coefficient for kth distribution. For estimating the parameters by the maximum log-likelihood method, compute p(X|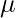 ,
, 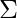 ,
, 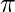 ).
).
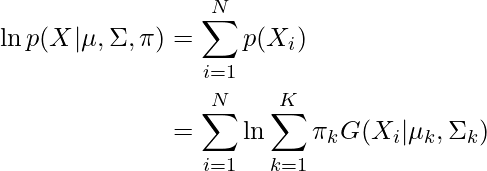
Now define a random variable 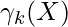 such that
such that 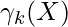 =p(k|X).
=p(k|X).
From Bayes theorem,

Now for the log-likelihood function to be maximum, its derivative of  with respect to
with respect to 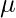 ,
, 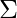 , and
, and 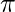 should be zero. So equating the derivative of
should be zero. So equating the derivative of  with respect to
with respect to 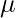 to zero and rearranging the terms,
to zero and rearranging the terms,
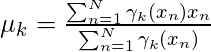
Similarly taking the derivative with respect to 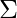 and pi respectively, one can obtain the following expressions.
and pi respectively, one can obtain the following expressions.
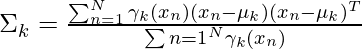
And

Note: 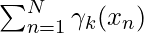 denotes the total number of sample points in the kth cluster. Here it is assumed that there is a total N number of samples and each sample containing d features is denoted by
denotes the total number of sample points in the kth cluster. Here it is assumed that there is a total N number of samples and each sample containing d features is denoted by 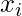 .
.
So it can be clearly seen that the parameters cannot be estimated in closed form. This is where the Expectation-Maximization algorithm is beneficial.
Expectation-Maximization (EM) Algorithm
The Expectation-Maximization (EM) algorithm is an iterative way to find maximum-likelihood estimates for model parameters when the data is incomplete or has some missing data points or has some hidden variables. EM chooses some random values for the missing data points and estimates a new set of data. These new values are then recursively used to estimate a better first date, by filling up missing points, until the values get fixed.
In the Expectation-Maximization (EM) algorithm, the estimation step (E-step) and maximization step (M-step) are the two most important steps that are iteratively performed to update the model parameters until the model convergence.
Estimation Step (E-step):
- In the estimation step, we first initialize our model parameters like the mean (μk), covariance matrix (Σk), and mixing coefficients (πk).
- For each data point, We calculate the posterior probabilities of data points belonging to each centroid using the current parameter values. These probabilities are often represented by the latent variables γk.
- At the end Estimate the values of the latent variables γ k based on the current parameter values
Maximization Step
- In the maximization step, we update parameter values ( i.e.
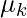 ,
, 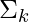 and
and ) using the estimated latent variable γk.
) using the estimated latent variable γk. - We will update the mean of the cluster point (μk) by taking the weighted average of data points using the corresponding latent variable probabilities
- We will update the covariance matrix (Σk) by taking the weighted average of the squared differences between the data points and the mean, using the corresponding latent variable probabilities.
- We will update the mixing coefficients (πk) by taking the average of the latent variable probabilities for each component.
Repeat the E-step and M-step until convergence
- We iterate between the estimation step and maximization step until the change in the log-likelihood or the parameters falls below a predefined threshold or until a maximum number of iterations is reached.
- Basically, in the estimation step, we update the latent variables based on the current parameter values.
- However, in the maximization step, we update the parameter values using the estimated latent variables
- This process is iteratively repeated until our model converges.
The Expectation-Maximization (EM) algorithm is a general framework and can be applied to various models, including Gaussian Mixture Models (GMMs). The steps described above are specifically for GMMs, but the overall concept of the Estimization-step and Maximization-step remains the same for other models that use the EM algorithm.
Implementation of the Gaussian Mixture Model
In this example, iris Dataset is taken. In Python, there is a Gaussian mixture class to implement GMM. Load the iris dataset from the datasets package. To keep things simple, take the only first two columns (i.e sepal length and sepal width respectively). Now plot the dataset.
Python3
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from pandas import DataFrame
from sklearn import datasets
from sklearn.mixture import GaussianMixture
iris = datasets.load_iris()
X = iris.data[:, :2]
d = pd.DataFrame(X)
plt.scatter(d[0], d[1])
plt.show()
|
Output:
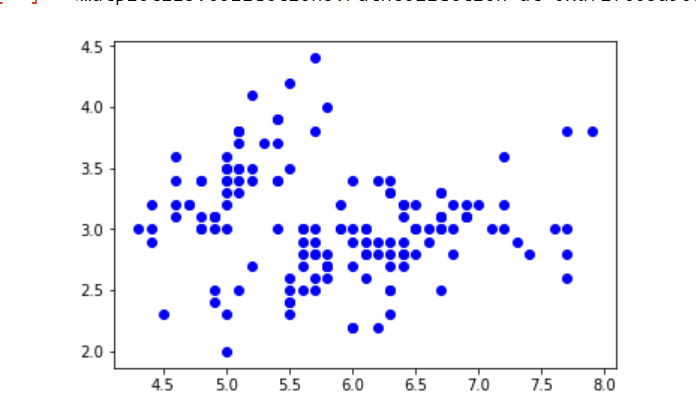
Iris dataset
Now fit the data as a mixture of 3 Gaussians. Then do the clustering, i.e assign a label to each observation. Also, find the number of iterations needed for the log-likelihood function to converge and the converged log-likelihood value.
Python3
gmm = GaussianMixture(n_components = 3)
gmm.fit(d)
labels = gmm.predict(d)
d['labels']= labels
d0 = d[d['labels']== 0]
d1 = d[d['labels']== 1]
d2 = d[d['labels']== 2]
plt.scatter(d0[0], d0[1], c ='r')
plt.scatter(d1[0], d1[1], c ='yellow')
plt.scatter(d2[0], d2[1], c ='g')
plt.show()
|
Output:
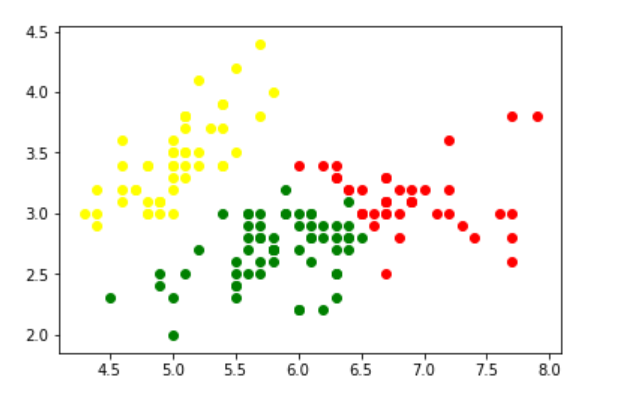
Clustering in the iris dataset using GMM
Print the converged log-likelihood value and no. of iterations needed for the model to converge
Python3
print(gmm.lower_bound_)
print(gmm.n_iter_)
|
Output:
-1.4985672470486966
8
Hence, it needed 7 iterations for the log-likelihood to converge. If more iterations are performed, no appreciable change in the log-likelihood value can be observed.
Share your thoughts in the comments
Please Login to comment...